Rapports anharmoniques
Prérequis
Résumé
Étant donnés quatre points alignés, on peut leur associer un nombre réel appelé leur rapport anharmonique. Il existe beaucoup de situations naturelles où quatre points particuliers ont un rapport anharmonique égal à $-1$ : on dit dans ce cas-là qu'ils forment une division harmonique. Ces notions peuvent se révéler très utiles pour prouver que trois points sont alignés ou que trois droites sont concourantes. Nous illustrons cela en démontrant notamment les théorèmes de Pascal, de Pappus et de Desargues.
Ce chapitre a été écrit par P. Alphonse et N. Radu et mis en ligne le 1 janvier 2018.
1. Définitions
Rapport anharmonique de $4$ points alignés
Étant donnés $4$ points distincts $A, B, C, D$ sur une même droite, on définit le rapport anharmonique $(A,B;C,D)$ comme suit. Rappelons que lorsque $X, Y, Z, T$ sont quatre points avec $XY$ parallèle à $ZT$, le rapport orienté $\frac{\overline{XY}}{\overline{ZT}}$ est défini comme étant égal à $\frac{|XY|}{|ZT|}$ ou $-\frac{|XY|}{|ZT|}$ selon que $[XY)$ et $[ZT)$ pointent dans le même sens ou non. La notion de rapport de section est également définie à partir de rapports orientés, voir le chapitre à ce sujet.Définition (rapport anharmonique de $4$ points)
Le rapport anharmonique de quatre points $A,B,C,D$ distincts alignés, aussi appelé birapport, est défini par
$$(A,B;C,D) = \frac{r_{DC}(A)}{r_{DC}(B)} = \frac{\frac{\overline{AC}}{\overline{AD}}}{\frac{\overline{BC}}{\overline{BD}}}.$$ Il dépend de l'ordre dans lequel les points $A, B, C, D$ sont considérés.
$$(A,B;C,D) = \frac{r_{DC}(A)}{r_{DC}(B)} = \frac{\frac{\overline{AC}}{\overline{AD}}}{\frac{\overline{BC}}{\overline{BD}}}.$$ Il dépend de l'ordre dans lequel les points $A, B, C, D$ sont considérés.
Comme toutes premières propriétés du rapport anharmonique, on peut voir que les formules suivantes sont vérifiées :
- $(B,A;C,D) = \dfrac{1}{(A,B;C,D)}$
- $(C,D;A,B) = (A,B;C,D)$
Lorsqu'on parle du rapport anharmonique $(A,B;C,D)$, on imagine souvent que $C$ et $D$ sont fixés et qu'on regarde la position de $A$ et $B$ par rapport à ces deux points $C$ et $D$ fixés. La deuxième égalité ci-dessus montre que regarder $A$ et $B$ par rapport à $C$ et $D$ revient en fait au même que regarder $C$ et $D$ par rapport à $A$ et $B$.
Division harmonique
Lorsque le rapport anharmonique de quatre points vaut $-1$, on parle de division harmonique :Définition (division harmonique)
On dit que quatres points alignés $A, B, C, D$ forment une division harmonique si $(A,B;C,D) = -1$. On dit aussi que $B$ est le conjugué harmonique de $A$ par rapport à $C,D$.
Dans le cas d'une division harmonique, il faut seulement préciser quelle paire de points (ici $A,B$) est comparée à quelle autre paire (ici $C,D$). En effet, $A, B, C, D$ forment une division harmonique si et seulement si l'une des quantités $(A,B;C,D)$, $(B,A;C,D)$, $(A,B;D,C)$, $(B,A;D,C)$, $(C,D;A,B)$, $(D,C;A,B)$, $(C,D;B,A)$, $(D,C;B,A)$ est égale à $-1$.
Si $C$ et $D$ sont fixés, alors tout point de la droite $CD$ (différent de $C$ et $D$) possède un unique conjugué harmonique par rapport à $C, D$, à l'exception du milieu $M$ de $[CD]$ qui n'en possède pas. De plus, le conjugué d'un point sur le segment $[CD]$ se trouve à l'extérieur de $[CD]$, et vice versa. Cela découle des propriétés du rapport de section : on a vu que la fonction $X \mapsto r_{DC}(X)$ définit une bijection entre les points de $DC$ différents de $D$ et les réels différents de $1$. Comme $r_{DC}(M) = -1$, $M$ ne possède pas de conjugué harmonique par rapport à $C,D$ : il n'existe aucun $X$ tel que $r_{DC}(X) = 1$.
Rapport anharmonique de $4$ droites concourantes
Il est aussi possible de définir le rapport anharmonique de $4$ droites concourantes. La définition se base sur la propriété suivante :Proposition (définition du rapport anharmonique de $4$ droites)
Soit $O$ un point et $a, b, c, d$ quatre droites distinctes passant par $O$. Soit $\ell$ une droite ne passant pas par $O$ et qui n'est pas parallèle à $a, b, c$ ou $d$. On note $A, B, C, D$ les intersections de $\ell$ avec $a, b, c$ et $d$. Alors le rapport anharmonique $(A,B;C,D)$ ne dépend pas de la droite $\ell$ choisie. Cette quantité est appelée le rapport anharmonique $(a,b;c,d)$ des droites $a, b, c, d$.
Démonstration
En utilisant la loi des sinus dans les triangles $OAC$, $OAD$, $OBC$ et $OBD$, on trouve la formule suivante, où les angles sont orientés :
$$(A,B;C,D) = \frac{\frac{\sin \widehat{AOC}}{\sin \widehat{AOD}}}{\frac{\sin\widehat{BOC}}{\sin\widehat{BOD}}}$$ Intuitivement la preuve est terminée, puisque cette quantité ne dépend pas de la droite $\ell$ choisie (mais uniquement des angles que les droites $a, b, c, d$ forment entre elles). Il y cependant une subtilité à laquelle il faut faire attention : chaque point $A$, $B$, $C$, $D$ peut se situer d'un côté de $O$ ou de l'autre (sur sa droite $a$, $b$, $c$, $d$). Les sinus des angles dans la formule ci-dessous, en valeur absolue, ne dépendent pas de la droite $\ell$, mais leurs signes peuvent changer ! Une analyse plus détaillée des cas montre toutefois que le signe de $(A,B;C,D)$ reste toujours le même, indépendamment de $\ell$.
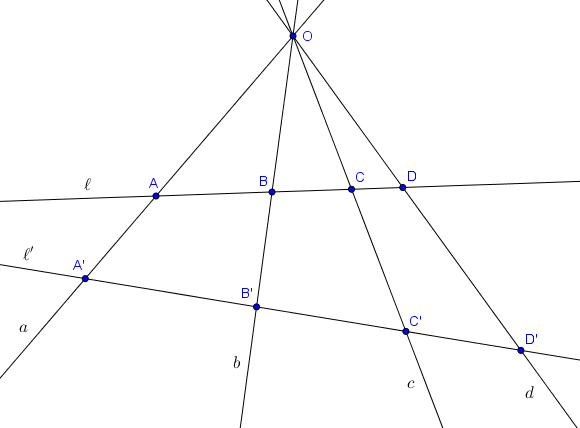
$$(A,B;C,D) = \frac{\frac{\sin \widehat{AOC}}{\sin \widehat{AOD}}}{\frac{\sin\widehat{BOC}}{\sin\widehat{BOD}}}$$ Intuitivement la preuve est terminée, puisque cette quantité ne dépend pas de la droite $\ell$ choisie (mais uniquement des angles que les droites $a, b, c, d$ forment entre elles). Il y cependant une subtilité à laquelle il faut faire attention : chaque point $A$, $B$, $C$, $D$ peut se situer d'un côté de $O$ ou de l'autre (sur sa droite $a$, $b$, $c$, $d$). Les sinus des angles dans la formule ci-dessous, en valeur absolue, ne dépendent pas de la droite $\ell$, mais leurs signes peuvent changer ! Une analyse plus détaillée des cas montre toutefois que le signe de $(A,B;C,D)$ reste toujours le même, indépendamment de $\ell$.

Faisceau harmonique
La définition suivante est l'équivalent de la division harmonique pour les droites concourantes :Définition (faisceau harmonique)
Quatre droites concourantes $a, b, c, d$ forment un faisceau harmonique si $(a,b;c,d) = -1$. On dira également que $a$ et $b$ sont conjugués harmoniques par rapport à $c,d$.
2. Dans la nature
Des divisions harmoniques apparaissent naturellement dans diverses situations.
Dans un triangle $ABC$, on peut prendre $d = AB$ et $d' = AC$, et le résultat nous indique que la bissectrice extérieure de $\hat A$ est conjuguée harmonique de la bissectrice intérieure de $\hat A$ par rapport aux deux côtés $AB$ et $AC$. Si $|AB| \neq |AC|$ et si $X$ (respectivement $Y$) désigne l'intersection de la bissectrice intérieure (respectivement extérieure) de $\hat A$ avec $BC$, on en déduit que $X, Y, B, C$ forment une division harmonique. Pour ceux ayant vu la théorie des cercles d'Apollonius, on peut voir ici un lien clair : on sait que les points $X$ et $Y$ appartiennent au $A$-cercle d'Apollonius, et la définition de ce cercle donne immédiatement que $X$ et $Y$ sont conjugués harmoniques par rapport à $B,C$.
Le lecteur averti aura deviné l'énoncé de la propriété suivante :
Il s'avère alors que chacune des trois diagonales est coupée harmoniquement par les deux autres :
Il est aussi possible de prouver la propriété ci-dessus en utilisant les théorèmes de Ceva et Ménélaüs. Mais il est également possible d'utiliser cette propriété pour démontrer Ceva à partir de Ménélaüs (ou le contraire).
$$\frac{|GO|}{|GE|} = \frac {2x}{x} = 2\quad \text{ et }\quad \frac{|HO|}{|HE|} = \frac{|GH|+|GO|}{|GH|-|GE|} = \frac{6x}{3x} = 2,$$ ce qui montre que $(G,H;O,E) = -1$.
Bissectrices intérieures et extérieures
La première illustration est très simple :Propriété (bissectrices)
Si $d$ et $d'$ sont deux droites sécantes, alors les deux bissectrices des angles qu'elles forment sont conjuguées harmoniques par rapport à $d, d'$.
Démonstration
Cela découle directement de la formule vue précédemment donnant le rapport anharmonique de $4$ droites en fonction des sinus des angles qu'elles forment entre elles.
Dans un triangle $ABC$, on peut prendre $d = AB$ et $d' = AC$, et le résultat nous indique que la bissectrice extérieure de $\hat A$ est conjuguée harmonique de la bissectrice intérieure de $\hat A$ par rapport aux deux côtés $AB$ et $AC$. Si $|AB| \neq |AC|$ et si $X$ (respectivement $Y$) désigne l'intersection de la bissectrice intérieure (respectivement extérieure) de $\hat A$ avec $BC$, on en déduit que $X, Y, B, C$ forment une division harmonique. Pour ceux ayant vu la théorie des cercles d'Apollonius, on peut voir ici un lien clair : on sait que les points $X$ et $Y$ appartiennent au $A$-cercle d'Apollonius, et la définition de ce cercle donne immédiatement que $X$ et $Y$ sont conjugués harmoniques par rapport à $B,C$.
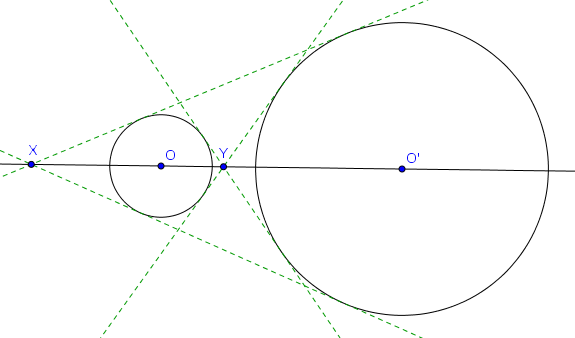
Tangentes à deux cercles
Considérons maintenant une toute autre situation : deux cercles $\mathcal{C}$ et $\mathcal{C}'$ extérieurs l'un à l'autre, de centres $O$ et $O'$ et de rayons différents. On dessine les quatre droites qui sont tangentes aux deux cercles, et on considère les intersections $X, Y$ qui se situent sur $OO'$ (voir figure ci-dessous).
Le lecteur averti aura deviné l'énoncé de la propriété suivante :
Propriété (tangentes à deux cercles)
Dans la configuration ci-dessus, les points $X$ et $Y$ sont conjugués harmoniques par rapport à $O, O'$, autrement dit $(X,Y;O,O') = -1$.
Démonstration
En considérant les points de tangences des droites considérées avec les deux cercles, on s'aperçoit immédiatement par triangles semblables que $\frac{|XO|}{|XO'|} = \frac{R}{R'}$ où $R$ et $R'$ sont les rayons des cercles $\mathcal{C}$ et $\mathcal{C}'$. De la même façon on obtient que $\frac{|YO|}{|YO'|} = \frac{R}{R'}$ également. Cela montre que $(X,Y;O,O') = -1$ (par la définition du rapport anharmonique de ces quatre points).
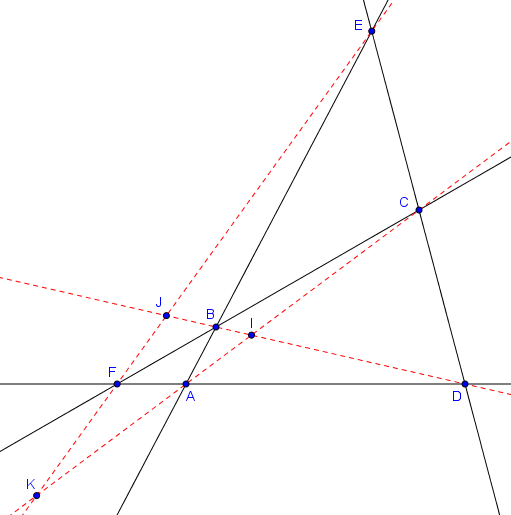
Quadrilatère complet
Un quadrilatère complet est un quadrilatère convexe $ABCD$ dont les côtés ne sont pas parallèles et auquel on ajoute l'intersection $E$ de $AB$ et $CD$ et l'intersection $F$ de $BC$ et $DA$, comme sur la figure ci-dessous. Une droite reliant deux des points $A, B, C, D, E, F$ et qui n'est pas déjà dessinée est alors appelée une diagonale du quadrilatère complet. Il y a trois diagonales : $AC$, $BD$ et $EF$.
Il s'avère alors que chacune des trois diagonales est coupée harmoniquement par les deux autres :
Proposition (quadrilatère complet)
Soit $A,B,C,D,E,F$ six points formant un quadrilatère complet comme ci-dessus. Désignons par $I$ l'intersection de $AC$ et $BD$, par $J$ l'intersection de $BD$ et $EF$, et par $K$ l'intersection de $EF$ et $AC$. Alors $(I,J;B,D) = -1$, $(J,K;E,F) = -1$ et $(K,I;A,C) = -1$.
Démonstration
Nous allons prouver que $(I,J,B,D) = -1$, les autres égalités ayant des preuves similaires.
Nous devons montrer que $I, J, B, D$ forment une division harmonique, et nous allons en fait montrer que les droites $EI$, $EJ$, $EB$, $ED$ forment un faisceau harmonique. Pour cela, considérons la droite $d$ passant par $E$ qui est la conjuguée harmonique de $EJ$ par rapport à $EB$ et $ED$. Il s'agirait de montrer que $d$ n'est autre que $EI$. Notons $X$ l'intersection de $d$ avec $BC$ et $Y$ l'intersection de $d$ avec $AD$. Comme les droites $d$, $EJ$, $EB$, $ED$ forment un faisceau harmonique, on déduit que $(X,F;B,C) = -1$ et $(Y,F;A,D) = -1$. Donc $(IX, IF; IB, IC) = -1$ et $(IY, IF; IA, ID) = -1$. La première égalité signifie que $IX$ est conjuguée harmonique de $IF$ par rapport à $IB, IC$, et la deuxième que $IY$ est conjuguée harmonique de $IF$ par rapport à $IA, ID$. Mais les paires $IB, IC$ et $IA, ID$ sont les mêmes, donc $IX$ et $IY$ sont toutes deux conjuguées harmoniques de $IF$ par rapport à la même paire de droite. Par unicité du conjugué harmonique, on en déduit que $IX = IY$, autrement dit $I$ se situe sur $XY = d$ comme voulu.
Nous devons montrer que $I, J, B, D$ forment une division harmonique, et nous allons en fait montrer que les droites $EI$, $EJ$, $EB$, $ED$ forment un faisceau harmonique. Pour cela, considérons la droite $d$ passant par $E$ qui est la conjuguée harmonique de $EJ$ par rapport à $EB$ et $ED$. Il s'agirait de montrer que $d$ n'est autre que $EI$. Notons $X$ l'intersection de $d$ avec $BC$ et $Y$ l'intersection de $d$ avec $AD$. Comme les droites $d$, $EJ$, $EB$, $ED$ forment un faisceau harmonique, on déduit que $(X,F;B,C) = -1$ et $(Y,F;A,D) = -1$. Donc $(IX, IF; IB, IC) = -1$ et $(IY, IF; IA, ID) = -1$. La première égalité signifie que $IX$ est conjuguée harmonique de $IF$ par rapport à $IB, IC$, et la deuxième que $IY$ est conjuguée harmonique de $IF$ par rapport à $IA, ID$. Mais les paires $IB, IC$ et $IA, ID$ sont les mêmes, donc $IX$ et $IY$ sont toutes deux conjuguées harmoniques de $IF$ par rapport à la même paire de droite. Par unicité du conjugué harmonique, on en déduit que $IX = IY$, autrement dit $I$ se situe sur $XY = d$ comme voulu.
Il est aussi possible de prouver la propriété ci-dessus en utilisant les théorèmes de Ceva et Ménélaüs. Mais il est également possible d'utiliser cette propriété pour démontrer Ceva à partir de Ménélaüs (ou le contraire).
Droite d'Euler
Dans le chapitre sur les transformations du plan, nous avons vu que la droite d'Euler d'un triangle est une droite particulière passant par le centre du cercle circonscrit $O$, l'orthocentre $H$, le centre de gravité $G$, mais aussi le centre du cercle d'Euler $E$. En fait, il s'avère que les points $G$, $H$, $O$, $E$ forment une division harmonique ! En effet, si on note $x = |GE|$, alors nous avons vu dans le chapitre en question que $|GO| = 2 \cdot |GE| = 2x$ et $|HG| = 2 \cdot |GO| = 4x$. Nous avons donc$$\frac{|GO|}{|GE|} = \frac {2x}{x} = 2\quad \text{ et }\quad \frac{|HO|}{|HE|} = \frac{|GH|+|GO|}{|GH|-|GE|} = \frac{6x}{3x} = 2,$$ ce qui montre que $(G,H;O,E) = -1$.
3. Théorèmes de Pascal et Pappus
Dans cette section nous expliquons comment les rapports anharmoniques peuvent être utilisés pour démontrer les théorèmes de Pascal et de Pappus. Cela nécessite d'abord de mettre en évidence quelques propriétés intéressantes des rapports anharmoniques.
Le théorème de Pascal tel qu'énoncé ci-dessus possède en fait une réciproque : si un hexagone est tel que les intersections des côtés opposés sont alignées, alors l'hexagone est inscrit dans une conique. Cela dépasse cependant le cadre de ce site : on s'intéresse rarement aux coniques autres que les cercles (et il n'est pas nécessaire de savoir ce qu'on entend par conique ici).
Dans les théorèmes de Pascal et de Pappus, on suppose que les intersections existent toujours. Nous allons voir dans la partie "plan projectif réel" de ce chapitre que ces conditions ne sont en fait pas nécessaires et que les théorèmes restent vrais dans les cas dégénérés.
Droites concourantes
Nous avons vu que deux droites sécantes à quatre mêmes droites concourantes donnent le même rapport anharmonique entre les points d'intersection. Ci-dessous nous formulons une sorte de réciproque qui peut se révéler bien pratique : si nous observons un même rapport anharmonique dans une situation bien précise, alors on peut en déduire que les droites reliant les points concernés sont concourantes.Proposition
Soit $\ell$ et $\ell'$ deux droites sécantes s'intersectant en $A$. Considérons $B, C, D$ trois points sur $\ell$ et $B',C',D'$ trois points sur $\ell'$. Si $(A,B;C,D) = (A,B';C',D')$, alors les droites $BB'$, $CC'$ et $DD'$ sont concourantes.
Démonstration
Notons $O$ le point d'intersection de $CC'$ et $DD'$, et désignons par $B''$ l'intersection de $OB$ avec $\ell'$. On sait que $(A,B;C,D) = (A,B'';C',D')$, et par hypothèse que $(A,B;C,D) = (A,B';C',D')$. Donc $(A,B';C',D') = (A,B'';C',D')$, et par unicité du conjugué harmonique on en déduit que $B' = B''$. Donc $O \in BB'$, ce qui montre que les trois droites $BB'$, $CC'$ et $DD'$ sont concourantes.
Rapport anharmonique sur un cercle
Lorsque quatre points $A, B, C, D$ appartiennent à un même cercle, on peut parler de leur rapport anharmonique $(A,B;C,D)$ grâce à la propriété suivante :Proposition (définition du rapport anharmonique de $4$ points cocycliques)
Soit $A, B, C, D$ quatre points sur un même cercle, et $P$ un cinquième point sur le cercle. Alors le rapport anharmonique $(PA, PB; PC, PD)$ ne dépend pas du point $P$ choisi. On parle alors du rapport anharmonique des quatre points cocycliques $A, B, C, D$.
Démonstration
Le sinus de $\widehat{APC}$ ne dépend pas de $P$ lorsque $P$ varie sur le cercle. Il en est de même pour $\sin \widehat{APD}$, $\sin \widehat{BPC}$ et $\sin \widehat{BPD}$, de sorte que la formule que nous avons vue avec les sinus donne toujours la même valeur pour $(PA, PB; PC, PD)$.
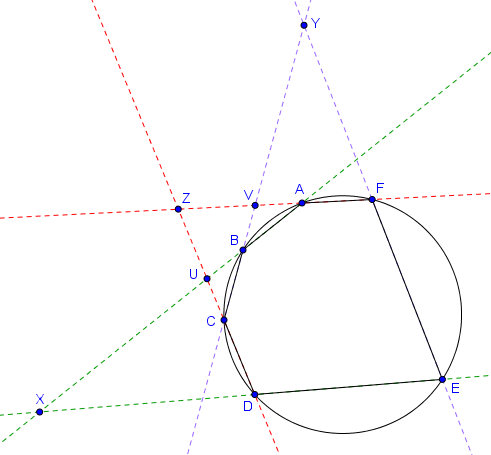
Théorème de Pascal
Le théorème de Pascal s'énonce comme suit, et possède une démonstration très simple en utilisant les rapports anharmoniques.Théorème de Pascal
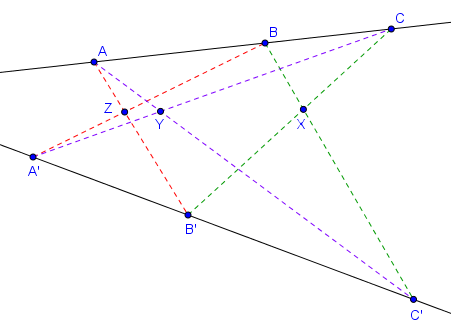
Soit $ABCDEF$ un hexagone inscrit dans un cercle, dont les côtés opposés ne sont pas parallèles. Désignons par $X$ l'intersection des côtés opposés $AB$ et $DE$, par $Y$ l'intersection des côtés opposés $BC$ et $EF$, et par $Z$ l'intersection des côtés opposés $CD$ et $FA$. Alors $X$, $Y$ et $Z$ sont alignés.

Démonstration
Le rapport anharmonique des quatre points cocycliques $A, E, C, B$ est à la fois égal à $(DA, DE; DC, DB)$ et à $(FA, FE; FC, FB)$. En considérant la droite $AB$ qui est sécante aux quatre droites $DA$, $DE$, $DC$ et $DB$, on trouve que $(DA, DE; DC, DB) = (A,X;U,B)$. D'autre part, en considérant la droite $BC$ qui est sécante aux quatre droites $FA$, $FE$, $FC$ et $FB$, on trouve que $(FA, FE; FC, FB) = (V,Y;C,B)$. On déduit des égalités obtenues que
$$(A,X;U,B) = (V,Y;C,B).$$ Le point $B$ est commun à ces deux rapports anharmoniques. Il découle donc de la propriété vue plus haut que les droites $AV$, $XY$ et $UC$ sont concourantes. Mais $AV$ et $UC$ s'intersectent en $Z$, donc cela signifie que $X$, $Y$ et $Z$ sont alignés.
$$(A,X;U,B) = (V,Y;C,B).$$ Le point $B$ est commun à ces deux rapports anharmoniques. Il découle donc de la propriété vue plus haut que les droites $AV$, $XY$ et $UC$ sont concourantes. Mais $AV$ et $UC$ s'intersectent en $Z$, donc cela signifie que $X$, $Y$ et $Z$ sont alignés.
Le théorème de Pascal tel qu'énoncé ci-dessus possède en fait une réciproque : si un hexagone est tel que les intersections des côtés opposés sont alignées, alors l'hexagone est inscrit dans une conique. Cela dépasse cependant le cadre de ce site : on s'intéresse rarement aux coniques autres que les cercles (et il n'est pas nécessaire de savoir ce qu'on entend par conique ici).
Théorème de Pappus
Le théorème de Pappus est très similaire au théorème de Pascal, sauf qu'au lieu d'avoir six points sur un cercle, on a trois points sur une droite et trois autres sur une autre droite. En fait, ces deux droites peuvent être vues comme une conique dégénérée (voir remarque précédente), mais ce n'est pas important pour nous.Théorème de Pappus
Soit $A, B, C$ trois points alignés, et $A', B', C'$ trois autres points alignés. Désignons par $X$ l'intersection de $BC'$ et $B'C$, par $Y$ l'intersection de $AC'$ et $A'C$, et par $Z$ l'intersection de $AB'$ et $A'B$ (pourvu qu'elles existent). Alors $X$, $Y$ et $Z$ sont alignés.

Démonstration
Nous donnons la démonstration dans le cas où les deux droites définies par $A, B, C$ et $A', B', C'$ sont sécantes en un point $P$. Dans la preuve du théorème de Pascal, on remplace les points $A, B, C, D, E, F$ par les points $A, B', C, A', B, C'$ respectivement. Pour que la même preuve donne le résultat, il suffit alors de voir que
$$(A'A, A'B; A'C, A'B') = (C'A, C'B; C'C, C'B'),$$ qui constituait la première étape de la preuve. Or on voit facilement que les quatre droites $A'A$, $A'B$, $A'C$ et $A'B'$ intersectent la droite définie par $A, B, C$ en les points $A$, $B$, $C$ et $P$ respectivement. Et il en est de même pour les quatre droites $C'A$, $C'B$, $C'C$ et $C'B'$, donc dans les deux cas la valeur du rapport anharmonique des quatre droites est $(A, B; C, P)$.
$$(A'A, A'B; A'C, A'B') = (C'A, C'B; C'C, C'B'),$$ qui constituait la première étape de la preuve. Or on voit facilement que les quatre droites $A'A$, $A'B$, $A'C$ et $A'B'$ intersectent la droite définie par $A, B, C$ en les points $A$, $B$, $C$ et $P$ respectivement. Et il en est de même pour les quatre droites $C'A$, $C'B$, $C'C$ et $C'B'$, donc dans les deux cas la valeur du rapport anharmonique des quatre droites est $(A, B; C, P)$.
Dans les théorèmes de Pascal et de Pappus, on suppose que les intersections existent toujours. Nous allons voir dans la partie "plan projectif réel" de ce chapitre que ces conditions ne sont en fait pas nécessaires et que les théorèmes restent vrais dans les cas dégénérés.
4. Théorème de Desargues
Le théorème de Desargues peut également se démontrer via les rapports anharmoniques :
On retiendra surtout de cette preuve que calculer le rapport anharmonique de quatre droites concourantes en considérant deux sécantes différentes peut souvent se révéler utile. Aussi, les rapports anharmoniques constituent clairement un outil puissant permettant de montrer que trois droites sont concourantes ou que trois points sont alignés. Les preuves des théorèmes de Pascal, Pappus et Desargues en sont de bons exemples.
Théorème de Desargues
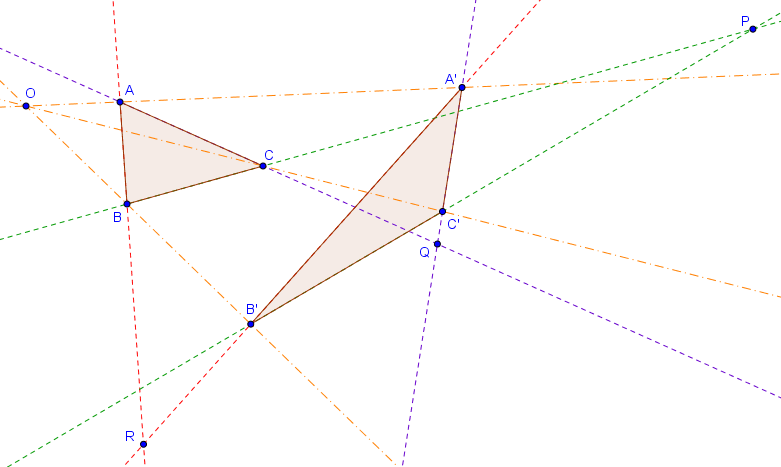
Soit $ABC$ et $A'B'C'$ deux triangles. Supposons que $BC$ et $B'C'$ s'intersectent en $P$, que $AC$ et $A'C'$ s'intersectent en $Q$, et que $AB$ et $A'B'$ s'intersectent en $R$. Alors les points $P, Q, R$ sont alignés si et seulement si les droites $AA'$, $BB'$ et $CC'$ sont concourantes ou parallèles.

Démonstration
Pour plus de simplicité nous supposerons que les droites en considération ne sont jamais parallèles.
- Supposons dans un premier temps que $AA'$, $BB'$ et $CC'$ sont concourantes en un point $O$. On désire montrer que $P$, $Q$ et $R$ sont alignés.
On calcule le rapport anharmonique des droites $RA$, $RA'$, $RO$ et $RQ$ de deux manières différentes, en considérant les sécantes $AA'$ et $BB'$. On trouve :
$$(A,A';O,AA' \cap RQ) = (RA, RA'; RO, RQ) = (B,B';O, BB' \cap RQ).$$ De façon similaire, on calcule le rapport anharmonique des droites $QA$, $QA'$, $QO$ et $QR$ de deux manières différentes, en considérant les sécantes $AA'$ et $CC'$ :
$$(A,A';O,AA'\cap QR) = (QA, QA'; QO, QR) = (C,C';O, CC' \cap QR).$$ On déduit des deux égalités précédentes que
$$(B,B';O, BB' \cap RQ) = (C,C';O, CC' \cap QR).$$ Le point $O$ étant commun à ces deux rapports anharmoniques, on en déduit que les droites $BC$, $B'C'$ et $JK$ sont concourantes, où $J = BB' \cap QR$ et $K = CC' \cap QR$. Clairement $JK = QR$, et comme l'intersection de $BC$ et $B'C'$ est $P$ par définition, on en déduit que $P$ se situe sur $QR$, comme voulu. - Nous montrons maintenant la réciproque. On suppose que $P, Q, R$ sont alignés, et on désire prouver que $AA'$, $BB'$ et $CC'$ sont concourantes. Nous désignons par $O$ l'intersection de $AA'$ et $BB'$, et notre but est de montrer que $CC'$ passe par $O$.
Comme ci-dessus, on a l'égalité
$$(A,A';O,AA' \cap RQ) = (RA, RA'; RO, RQ) = (B,B';O, BB' \cap RQ).$$ D'autre part, si on calcule le rapport anharmonique des droites $QA$, $QA'$, $QO$ et $QR$ à partir des sécantes $AA'$ et $CO$, on obtient
$$(A,A';O,AA'\cap QR) = (QA, QA'; QO, QR) = (C,CO \cap QA';O, CO \cap QR).$$ Finalement, le rapport anharmonique des droites $PB$, $PB'$, $PO$ et $PQ$ se calcule à partir des sécantes $BB'$ et $CO$ et on trouve
$$(B,B';O,BB' \cap PQ) = (PB,PB';PO,PQ) = (C,CO \cap PB'; O, CO \cap PQ).$$ En utilisant les trois égalités précédentes, on obtient que
$$(C,CO \cap QA';O, CO \cap QR) = (C,CO \cap PB'; O, CO \cap PQ),$$ ce qui signifie que $CO \cap QA' = CO \cap PB'$. Les droites $CO$, $QA'$ et $PB'$ sont donc concourantes. Mais $QA' \cap PB' = C'$, donc cela signifie que $CO$ passe par $C'$. Par conséquent, $C$, $C'$ et $O$ sont alignés comme espéré.
On retiendra surtout de cette preuve que calculer le rapport anharmonique de quatre droites concourantes en considérant deux sécantes différentes peut souvent se révéler utile. Aussi, les rapports anharmoniques constituent clairement un outil puissant permettant de montrer que trois droites sont concourantes ou que trois points sont alignés. Les preuves des théorèmes de Pascal, Pappus et Desargues en sont de bons exemples.
5. Plan projectif réel
Les énoncés des résultats de ce chapitre ne sont pas tout à fait satisfaisants. En effet, chaque énoncé requiert l'hypothèse que certaines droites ne sont pas parallèles, de sorte qu'on puisse parler de leur point d'intersection. Les choses ne seraient-elles pas plus simples dans un monde où deux droites ne sont jamais parallèles et possèdent toujours un point d'intersection ? En fait, un tel monde existe : il s'appelle le plan projectif réel !
L'idée est donc de partir du plan euclidien et de lui rajouter des points (abstraits) pour que les droites parallèles aient enfin un point d'intersection. Étant donnée une "direction de droite", on va donc ajouter un point "à l'infini dans cette direction" et dire que toutes les droites dans cette direction passent par ce point ! (On dit que deux droites ont la même direction lorsqu'elles sont parallèles.) Étant données deux droites, on a donc deux possibilités :
Il y a cependant un petit souci dans la modification que nous avons apportée au plan euclidien. En effet, nous avons fait en sorte que le point 2 ci-dessus soit vérifié, c'est-à-dire que deux droites possèdent toujours un unique point d'intersection, mais le point 1 n'est maintenant plus vérifié ! En effet, nous avons introduit de nouveaux points, et si nous considérons maintenant deux points à l'infini (dans des directions différentes), alors il n'existe pour le moment aucune droite passant par ces deux points ! Pour régler ce problème, on est dans l'obligation de rajouter une nouvelle droite à notre plan, appelée la "droite à l'infini". Par définition, cette droite à l'infini passe par tous les points à l'infini (et elle ne passe par aucun point du plan euclidien habituel). Grâce à cette nouvelle droite, le point 1 est maintenant à nouveau vérifié, et on peut voir que le point 2 reste également vrai.
Pour résumer, les points et les droites du plan projectif réel sont les suivants :
Attention : Sauf mention explicite du contraire, nous ne supposons jamais sur ce site être dans le plan projectif réel ! En particulier, nous considérons toujours que deux droites parallèles ne s'intersectent pas.
Définition du plan projectif réel
Nous aimerions être en présence d'un plan où les deux conditions suivantes sont vérifiées :- Étant donnés deux points du plan, il existe toujours une unique droite passant par ces deux points.
- Étant données deux droites du plan, il existe toujours un unique point appartenant à ces deux droites.
L'idée est donc de partir du plan euclidien et de lui rajouter des points (abstraits) pour que les droites parallèles aient enfin un point d'intersection. Étant donnée une "direction de droite", on va donc ajouter un point "à l'infini dans cette direction" et dire que toutes les droites dans cette direction passent par ce point ! (On dit que deux droites ont la même direction lorsqu'elles sont parallèles.) Étant données deux droites, on a donc deux possibilités :
- soit elles sont sécantes (dans le plan euclidien habituel) et elles ont pour point commun leur point d'intersection habituel,
- soit elles sont parallèles, et elles ont alors pour point commun le point à l'infini dans la direction qu'elles définissent.
Il y a cependant un petit souci dans la modification que nous avons apportée au plan euclidien. En effet, nous avons fait en sorte que le point 2 ci-dessus soit vérifié, c'est-à-dire que deux droites possèdent toujours un unique point d'intersection, mais le point 1 n'est maintenant plus vérifié ! En effet, nous avons introduit de nouveaux points, et si nous considérons maintenant deux points à l'infini (dans des directions différentes), alors il n'existe pour le moment aucune droite passant par ces deux points ! Pour régler ce problème, on est dans l'obligation de rajouter une nouvelle droite à notre plan, appelée la "droite à l'infini". Par définition, cette droite à l'infini passe par tous les points à l'infini (et elle ne passe par aucun point du plan euclidien habituel). Grâce à cette nouvelle droite, le point 1 est maintenant à nouveau vérifié, et on peut voir que le point 2 reste également vrai.
Pour résumer, les points et les droites du plan projectif réel sont les suivants :
- Les points du plan projectif réel sont les points du plan euclidien + pour chaque direction de droite, un point à l'infini dans cette direction.
- Les droites du plan projectif réel sont les droites du plan euclidien + la droite à l'infini, qui passe par tous les points à l'infini.
En pratique
Lorsqu'on se place dans le plan projectif réel, la plupart des énoncés deviennent plus simples (et parfois même plus généraux).- Étant donnés deux points $C, D$, on a vu que $X \mapsto r_{DC}(X)$ définissait une bijection entre les points de $CD$ différents de $C$ et $D$ et les réels non-nuls et différents de $1$. Si $P$ désigne le point à l'infini de $CD$, il est en fait naturel de définir $r_{DC}(P) = 1$. Le rapport anharmonique $(A,B;C,D)$ est alors également défini lorsqu'un des points $A, B, C, D$ est le point à l'infini de la droite considérée. (S'il s'agit de $A$ ou $B$ on utilise que $r_{DC}(P) = 1$ ; s'il s'agit de $C$ ou $D$ on peut utiliser que $(A,B;C,D) = (C,D;A,B)$ et se ramener au cas précédent.) De cette manière, le milieu $M$ de $[CD]$ dont on avait dit qu'il n'avait pas de conjugué harmonique (par rapport à $C,D$) en a maintenant un : il s'agit du point $P$ à l'infini de $CD$. On peut voir que les différents résultats concernant les rapports anharmoniques restent vrais avec cette convention.
- Pour définir le rapport anharmonique de $4$ droites concourantes en $O$, on considérait une autre droite ne passant pas par $O$ et sécante aux $4$ droites. Cette deuxième condition n'est maintenant plus nécessaire : on peut prendre n'importe quelle droite ne passant pas par $O$. Si elle est parallèle à l'une des quatre droites, alors son intersection avec celle-ci est son point à l'infini.
- Dans notre exemple des points d'intersection des quatre tangentes à deux cercles, on supposait que les deux cercles avaient des rayons différents. En fait, si les cercles ont même rayon, alors les points d'intersection $X$ et $Y$ sont respectivement le point à l'infini de $OO'$ et le milieu de $[OO']$. Le résultat est donc toujours vrai : les points $X$ et $Y$ sont conjugués harmoniques par rapport à $O,O'$.
- Dans tous les résultats où on demandaient que des droites ne soient pas parallèles, on peut supprimer cette hypothèse. Par exemple :
- Le théorème de Pascal peut s'énoncer comme suit :
Théorème de PascalSoit $ABCDEF$ un hexagone inscrit à un cercle. Désignons par $X$ l'intersection des côtés opposés $AB$ et $DE$, par $Y$ l'intersection des côtés opposés $BC$ et $EF$, et par $Z$ l'intersection des côtés opposés $CD$ et $FA$. Alors $X$, $Y$ et $Z$ sont alignés.
Les points $X$, $Y$ et/ou $Z$ peuvent en fait être des points à l'infini. Par exemple, si $X$ est un point à l'infini et $Y$ et $Z$ sont des points "normaux", alors dire que $X, Y, Z$ sont alignés signifie que la direction de $YZ$ est donnée par le point à l'infini $X$. Autrement dit, dans ce cas les droites $AB$ et $DE$ sont parallèles (d'intersection $X$ à l'infini), et le fait que $Y$ et $Z$ sont alignés avec $X$ signifie que $YZ$ est parallèle à $AB$ et $DE$. Notre nouvel énoncé du théorème de Pascal est donc plus général puisqu'il traite également des cas où certains côtés sont parallèles. - De même, dans le théorème de Pappus on peut enlever la condition "pourvu que les intersections existent" :
Théorème de PappusSoit $A, B, C$ trois points alignés, et $A', B', C'$ trois autres points alignés. Désignons par $X$ l'intersection de $BC'$ et $B'C$, par $Y$ l'intersection de $AC'$ et $A'C$, et par $Z$ l'intersection de $AB'$ et $A'B$. Alors $X$, $Y$ et $Z$ sont alignés.
Là aussi les points $X$, $Y$ et/ou $Z$ peuvent être des points à l'infini. - Le théorème de Desargues n'a également pas besoin de toutes les hypothèses que nous avons données précédemment :
Théorème de DesarguesSoit $ABC$ et $A'B'C'$ deux triangles. Soit $P$ l'intersection de $BC$ et $B'C'$, $Q$ l'intersection de $AC$ et $A'C'$, et $R$ l'intersection de $AB$ et $A'B'$. Alors les points $P, Q, R$ sont alignés si et seulement si les droites $AA'$, $BB'$ et $CC'$ sont concourantes.
Nous avons ici remplacé la fin "concourantes ou parallèles" par simplement "concourantes". En effet, dans le plan projectif trois droites parallèles sont concourantes puisqu'elles s'intersectent en leur point à l'infini !
- Le théorème de Pascal peut s'énoncer comme suit :
Attention : Sauf mention explicite du contraire, nous ne supposons jamais sur ce site être dans le plan projectif réel ! En particulier, nous considérons toujours que deux droites parallèles ne s'intersectent pas.