Concours > Concours #20
Description
Pour fêter l'arrivée de $2026$ comme il se doit, dix vaillants correcteurs se sont réunis pour vous concocter un nouveau concours ! Celui-ci réunira dix problèmes couvrant toutes les matières et ordonnés par difficulté croissante. Tout le monde devrait pouvoir y trouver du plaisir, que ce soit les étudiants au début de leur parcours olympique comme les plus affutés.
Un nouveau problème fera son apparition chaque soir et restera accessible pendant deux jours, jusqu'au tant redouté Problème #10 qui accompagnera les plus motivés jusqu'au début du réveillon.
Un nouveau problème fera son apparition chaque soir et restera accessible pendant deux jours, jusqu'au tant redouté Problème #10 qui accompagnera les plus motivés jusqu'au début du réveillon.
Organisateurs du concours : 13Corentin Bodart, 8Antoine D., 4Félix Houdouin, 9Michel J., 8Simon Jégou, 8Rémi Lesbats, 9Pierre Montperrus, 5Solal Pivron-Djeddi, 5Mathieu P. et 12Nicolas Radu.
Problème #1 |
|
Solutions acceptées du samedi 20 décembre 2025 à 18h00 au lundi 22 décembre 2025 à 18h00 (heures belges).
ÉnoncéStatistiquesScores parfaits : 166
Origine du problème : Création originale (Antoine D.)
|
Problème #2 |
|
Solutions acceptées du dimanche 21 décembre 2025 à 18h00 au mardi 23 décembre 2025 à 18h00 (heures belges).
ÉnoncéStatistiquesScores parfaits : 139
Origine du problème : Cordoba pre-TST Cono Sur 2014, Problème 2
|
Problème #3 |
|
Solutions acceptées du lundi 22 décembre 2025 à 18h00 au mercredi 24 décembre 2025 à 18h00 (heures belges).
Énoncé$$u_{n+3}=\frac{u_n u_{n+2}}{u_{n+1}} \quad \text{pour tout $n \ge 1$},$$ que $u_{25}$ et $u_{75}$ sont entiers, et que $u_{50}=u_{100}$. Montrer que $$u_1^{2026}+u_2^{2026}+ \ldots +u_{99}^{2026}+u_{100}^{2026}$$ est un carré parfait. StatistiquesScores parfaits : 208
Origine du problème : Slovak Mathematical Olympiad 2005/2006, Catégorie A, Régional, Problème 2 (modifié)
|
Problème #4 |
|
Solutions acceptées du mardi 23 décembre 2025 à 18h00 au jeudi 25 décembre 2025 à 18h00 (heures belges).
ÉnoncéStatistiquesScores parfaits : 107
Origine du problème : Création originale (Nicolas Radu)
|
Problème #5 |
|
Solutions acceptées du mercredi 24 décembre 2025 à 18h00 au vendredi 26 décembre 2025 à 18h00 (heures belges).
ÉnoncéMontrer que pour tout $n \ge 7$, il existe exactement un $n$-uple auto-référent. StatistiquesScores parfaits : 27
Origine du problème : Création originale (Pablo Espana Gutierrez)
|
Problème #6 |
|
Solutions acceptées du jeudi 25 décembre 2025 à 18h00 au samedi 27 décembre 2025 à 18h00 (heures belges).
Énoncé$$\ppcm(a,b)+\ppcm(a+1,b+1)>\frac{2 a b} {\sqrt{|a-b|}}.$$ StatistiquesScores parfaits : 123
Origine du problème : Art of Problem Solving
|
Problème #7 |
|
Solutions acceptées du vendredi 26 décembre 2025 à 18h00 au dimanche 28 décembre 2025 à 18h00 (heures belges).
ÉnoncéStatistiquesScores parfaits : 55
Origine du problème : GGG4, Problème 1
|
Problème #8 |
|
Solutions acceptées du samedi 27 décembre 2025 à 18h00 au lundi 29 décembre 2025 à 18h00 (heures belges).
Énoncé$$f(xf(y) + y^2) = (x + y)f(x) + (x + f(y))f(y - x).$$ StatistiquesScores parfaits : 47
Origine du problème : India-Iran-Singapore-Taiwan Friendly Contest 2025
|
Problème #9 |
|
Solutions acceptées du dimanche 28 décembre 2025 à 18h00 au mardi 30 décembre 2025 à 18h00 (heures belges).
Énoncé\[ \forall m,n\in S,\quad m\mid n\implies \bigl( f(m)\mid f(n)\text{ ou }f(n)\mid f(m)\bigr).\] Montrer que $f(p)$ est premier pour tout $p\in S$ premier. StatistiquesScores parfaits : 26
Origine du problème : Création originale (Corentin Bodart et Quentin Claus)
|
Problème #10 |
|
Solutions acceptées du lundi 29 décembre 2025 à 18h00 au mercredi 31 décembre 2025 à 18h00 (heures belges).
Énoncé
Par exemple, voici une $5$-coloration valide qui est $4$-valide mais n'est pas $3$-valide. 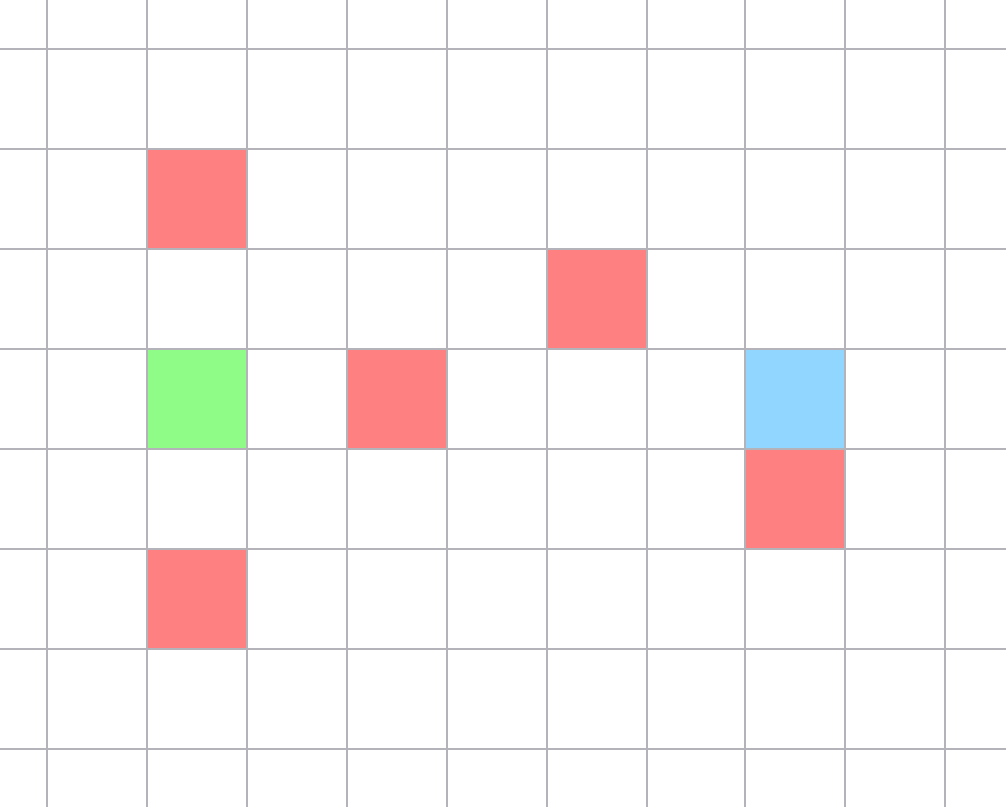 StatistiquesScores parfaits : 6
Origine du problème : Israel National Olympiad 2024, Problème 7 (modifié)
|