Processing

Théorie > Géométrie > Triangles

Général
Résumé Chapitre entier
Points théoriques
Lois des sinus et des cosinus Droites et points particuliers Aire d'un triangle Propriétés diverses
Exercices
Exercice 1 Exercice 2 Exercice 3 Exercice 4 Exercice 5 Exercice 6 Exercice 7

Lois des sinus et des cosinus

Loi des sinus

La loi des sinus est fondamentale. Dans celle-ci, il est important de retenir la dernière égalité, parfois oubliée par les élèves.

Loi des sinus
Soit ABC un triangle de côtés a=|BC|, b=|AC| et c=|AB|. On a
asinA=bsinB=csinC=2R, où R désigne le rayon du cercle circonscrit au triangle ABC.

Démonstration
On va simplement montrer que asinA=2R. On aura bien sûr les mêmes égalités avec b et c.

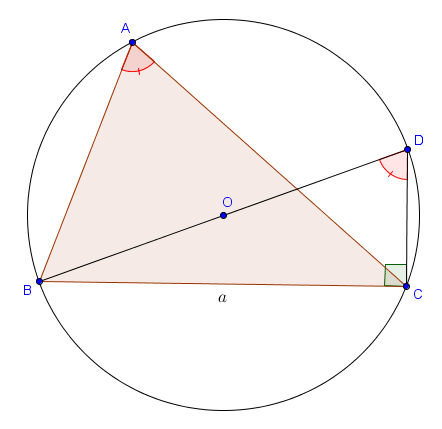
On trace le cercle circonscrit à ABC et note D le point de ce cercle tel que [BD] en soit un diamètre. On a alors ^BAC=^BDC (angles inscrits), et on en déduit que
asinA=|BC|sin^BAC=|BC|sin^BDC=|BD|, où la dernière égalité vient du fait que le triangle BCD est rectangle en C (car il est inscrit dans un demi-cercle). Puisque |BD|=2R, la démonstration est terminée.

Loi des cosinus

La loi des cosinus est aussi connue sous le nom de théorème de Pythagore généralisé, ou encore théorème d'Al-Kashi. Il s'agit en fait d'une généralisation du théorème de Pythagore aux triangles non nécessairement rectangles.

Loi des cosinus
Soit ABC un triangle de côtés a=|BC|, b=|AC| et c=|AB|. On a
c2=a2+b2−2abcosC.

Nous donnons la démonstration dans le cas où ABC est acutangle. Elle est totalement analogue lorsque le triangle est obtusangle, il faut juste discuter plusieurs cas.

Démonstration (cas acutangle)
On note P le pied de la hauteur de ABC issue de A, et h=|AP|, d=|CP|. On peut alors appliquer Pythagore au triangle APB pour obtenir :
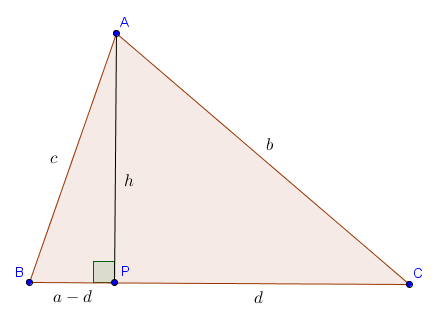
c2=h2+(a−d)2=h2+a2+d2−2ad. Or, on a aussi h2+d2=b2 par Pythagore dans le triangle APC, d'où
c2=b2+a2−2ad. Il ne reste alors plus qu'à constater que d=bcosC, ce qui nous donne finalement
c2=a2+b2−2abcosC.