Concours > Concours #18

Description

En cette période de grandes vacances, rien de mieux qu'une nouvelle édition des concours de l'été pour s'occuper ! Notre équipe de français motivés vous invite à découvrir une sélection de divers exercices, pour la plupart inventés par nos soins. Vous êtes conviés à tenter votre chance face à ces problèmes de difficulté variable : il y en aura pour tous les goûts !

Le concours sera composé de $10$ problèmes, classés par ordre de difficulté croissante, et chacun sera disponible pendant $2$ jours. Les premiers problèmes ont été conçus pour être abordables par tous, en revanche seuls les vrais guerriers pourront venir à bout des derniers 3:[. Tous les thèmes seront représentés parmi les premiers exercices comme parmi les derniers, donc tout le monde devrait y trouver son compte !

Nous vous souhaitons bon courage, en espérant que vous apprécierez ces problèmes :-D

Organisateurs du concours : Serge B., Anatole Bouton, Gaëtan Dautzenberg, 8Rémi Lesbats, Auguste Ramondou, Georges T. et 3Melvil Treilleux.

Problème #1

Solutions acceptées du mercredi 26 juillet 2023 à 12h00 au vendredi 28 juillet 2023 à 12h00 (heures belges).
Énoncé
Trouver tous les triplets de réels strictement positifs $(a,b,c)$ tels que
$$(a+b)\left(\frac 1b+\frac 1c\right)=(b+c)\left(\frac 1c+\frac 1a\right)=(c+a)\left(\frac 1a+\frac 1b\right)=4.$$
Statistiques
Tenté par 273 personnes
Scores parfaits : 199
Origine du problème : Création originale (Gaëtan Dautzenberg)

Problème #2

Solutions acceptées du jeudi 27 juillet 2023 à 12h00 au samedi 29 juillet 2023 à 12h00 (heures belges).
Énoncé
Trouver tous les entiers naturels $n \geqslant 3$ tels qu'il existe $n$ réels non nuls que l'on peut disposer sur un cercle de telle sorte que chacun d'entre eux soit la somme de ses deux voisins.
Statistiques
Tenté par 234 personnes
Scores parfaits : 149
Origine du problème : Création originale (Anatole Bouton)

Problème #3

Solutions acceptées du vendredi 28 juillet 2023 à 12h00 au dimanche 30 juillet 2023 à 12h00 (heures belges).
Énoncé
Trouver tous les couples d'entiers positifs ou nuls $(x,y)$ tels que :
$$x^4-6x^2+1=7\cdot 2^y.$$
Statistiques
Tenté par 235 personnes
Scores parfaits : 203
Origine du problème : Olimpíada Matemáticos por Diversão 2020

Problème #4

Solutions acceptées du samedi 29 juillet 2023 à 12h00 au lundi 31 juillet 2023 à 12h00 (heures belges).
Énoncé
Soit $ABC$ un triangle dont tous les angles sont aigus, et $H$ son orthocentre. La tangente en $H$ au cercle circonscrit à $BHC$ coupe le cercle circonscrit à $ABC$ en $U$ et $V$. Montrer que $|AU| = |AV|$.
Statistiques
Tenté par 153 personnes
Scores parfaits : 123
Origine du problème : Création originale (Anatole Bouton)

Problème #5

Solutions acceptées du dimanche 30 juillet 2023 à 12h00 au mardi 1 août 2023 à 12h00 (heures belges).
Énoncé
Au pays des lutins maléfiques, il y a un nombre pair d'habitants, et chacun a un nombre pair d'amis (personne n'est ami avec soi-même, et l'amitié est réciproque). Si Rémi est un habitant de ce pays, montrer qu’il existe un autre habitant qui a un nombre pair d'amis en commun avec Rémi.
Statistiques
Tenté par 171 personnes
Scores parfaits : 149
Origine du problème : Inspiré de 102 combinatorial problems, Problème 38

Problème #6

Solutions acceptées du lundi 31 juillet 2023 à 12h00 au mercredi 2 août 2023 à 12h00 (heures belges).
Énoncé
Trouver tous les polynômes $P$ à coefficients entiers tels qu'il existe des entiers strictement positifs $a< b< c< d$ vérifiant la propriété suivante : pour tout entier strictement positif $k$, on a $P(ak)+P(bk)\ne0$ et
$$P(ak)+P(bk)\mid P(ck)+P(dk).$$
Statistiques
Tenté par 131 personnes
Scores parfaits : 58
Origine du problème : Création originale (Gaëtan Dautzenberg)

Problème #7

Solutions acceptées du mardi 1 août 2023 à 12h00 au jeudi 3 août 2023 à 12h00 (heures belges).
Énoncé
Trouver toutes les fonctions $f : \mathbb{R} \rightarrow \mathbb{R}$ telles que
$$f(x^2-f(y)^2) = xf(x) -y^2 \ \text{ pour tous $x, y \in \mathbb{R}$.}$$
Statistiques
Tenté par 162 personnes
Scores parfaits : 95
Origine du problème : 169 functional equations, Problème 56

Problème #8

Solutions acceptées du mercredi 2 août 2023 à 12h00 au vendredi 4 août 2023 à 12h00 (heures belges).
Énoncé
Soit $ABC$ un triangle, et $D$ le pied de la bissectrice issue de $A$. Soient $\omega _1$ et $\omega _2$ les cercles passant par $A$ et de centres $B$ et $C$ respectivement. On note $E$ et $F$ les secondes intersections respectives de $\omega _1$ et $\omega _2$ avec $AD$. Soit $M$ le milieu de $[AF]$. On suppose que $E\neq M$ et on considère $\Gamma$ le cercle circonscrit au triangle $BEM$. On appelle $P$ la deuxième intersection de $\Gamma$ avec $\omega_1$. Montrer que le cercle circonscrit au triangle $PDF$ rencontre $\Gamma$ sur $BC$.
Statistiques
Tenté par 73 personnes
Scores parfaits : 46
Origine du problème : Création originale (Auguste Ramondou)

Problème #9

Solutions acceptées du jeudi 3 août 2023 à 12h00 au samedi 5 août 2023 à 12h00 (heures belges).
Énoncé
Un terrible drame vient de survenir au pays des lutins maléfiques : Nicolas le Renégat a enlevé les $n\geqslant 2$ lutins de la 1ère garnison ! Il compte utiliser son $2n-$gone régulier démoniaque pour en tuer le plus possible. Magnanime, il laisse les lutins choisir leurs positions sur les sommets du $2n-$gone (il doit y avoir au plus un lutin sur chaque sommet, et chaque lutin doit être sur un sommet). Puis Nicolas place une bombe à lutins sur chacun des $n$ sommets restés libres. Enfin, il choisit une droite $d$ passant par les milieux de deux côtés opposés du $2n-$gone régulier et chaque bombe à lutin est catapultée sur son symétrique par rapport à $d$. Chaque fois qu'une bombe atterrit sur un lutin, celui-ci meurt sur le coup. Les autres lutins peuvent repartir sains et saufs. En sachant que Nicolas est un sanguinaire qui cherche à tuer le plus de lutins possible, combien d'entre eux survivront au maximum ?
Par exemple, pour $n=4$, si les lutins choisissent de se placer comme sur le schéma ci-dessous, Nicolas dispose de la droite $d$ marquée en rouge qui lui permet d'éradiquer tous les lutins ! Peut-être était-il possible pour eux de se positionner autrement sur l'octogone pour en sauver quelques-uns ?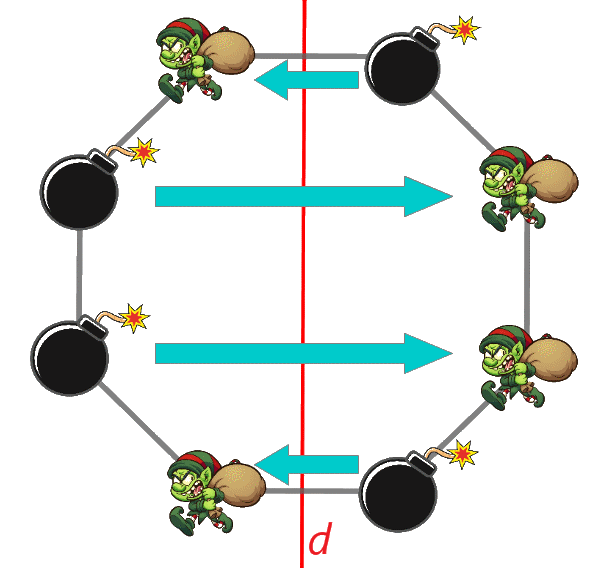

Statistiques
Tenté par 74 personnes
Scores parfaits : 17
Origine du problème : Création originale (Auguste Ramondou & Anatole Bouton)

Problème #10

Solutions acceptées du vendredi 4 août 2023 à 12h00 au dimanche 6 août 2023 à 12h00 (heures belges).
Énoncé
Cher participant au Concours #18, l’équipe des organisateurs a besoin de vous ! Nous avons été trahis par Rémi qui s’est avéré être un lutin maléfique, et qui nous a enfermés dans une cellule de la prison magique dans laquelle vous vous trouvez. Dans cette prison, chaque cellule possède un numéro entier, et chaque entier strictement positif est le numéro d'une unique cellule. Dans la cellule $k$ se trouvent les clés des cellules $\varphi(k), \sigma(k)$ et $\tau(k)$. Nous vous transmettons de plus avec cette lettre la clé de la cellule $a\geqslant 2$ que nous avons réussi à subtiliser à Rémi.
En sachant que nous sommes cachés dans la cellule $b\geqslant 1$, montrez que vous pouvez nous sauver de l'infâme Rémi et nous vous récompenserons d'un généreux $7/7$ !

Vous aurez besoin des définitions des fonctions $\varphi$, $\sigma$ et $\tau$ afin de mener à bien votre mission. Pour tout entier $n\geqslant 2$, on note :
  • $\varphi(n)$ le nombre d'entiers naturels inférieurs à $n$ qui sont premiers avec $n$ ;
  • $\sigma(n)$ la somme des diviseurs positifs de l'entier $n$ ;
  • $\tau(n)$ le nombre de diviseurs positifs de l'entier $n$.
Statistiques
Tenté par 45 personnes
Scores parfaits : 9
Origine du problème : ELMO 2020, Problème 6 (recontextualisé)