Théorie > Fondements > Rédaction d'une preuve
Prérequis
Aucun prérequis.
Résumé
Toutes les mathématiques reposent sur des démonstrations. Lorsqu'on affirme quelque chose, il s'agit en effet de le prouver par un raisonnement logique. La preuve est en quelque sorte le moyen de communication principal des mathématiciens ! Savoir rédiger une preuve est donc primordial pour pouvoir partager ses observations et découvertes, et nous donnons dans ce chapitre toutes les clefs pour écrire une bonne démonstration.
Ce chapitre a été écrit par N. Radu et mis en ligne le 12 octobre 2023.
1. Conseils généraux
Rédiger une solution à un problème est une étape essentielle dans la résolution de celui-ci. Avoir une idée de la solution dans votre tête est une chose, mais c'est en la rédigeant que vous pourrez partager votre savoir, le faire vérifier, et recevoir des commentaires. Une bonne rédaction est primordiale pour transmettre ses idées de la façon la plus efficace possible. Au contraire, une mauvaise rédaction peut rendre votre solution illisible, ou même complètement fausse !
Pour savoir si la preuve que vous écrivez est bonne, vous pouvez essayer de vous mettre à la place de quelqu'un ayant les mêmes connaissances mathématiques que vous et qui découvrirait votre preuve pour la première fois. Cette personne fictive vient de découvrir le résultat que vous cherchez à démontrer, n'a même aucune idée de si ce résultat est vrai ou non, et la preuve qu'il s'apprête à lire doit le convaincre à $100\%$ que ce résultat est bien vrai. Cette personne est d'un naturel sceptique et tient à ce que tout soit très clairement justifié pour être pleinement convaincue. Elle est aussi pressée et ne tient pas à devoir réfléchir trois minutes à chaque argument pour comprendre comment il s'applique. Il faut donc que tout coule de source !
Notez bien que votre ami imaginaire ne lit pas dans vos pensées ! De votre côté, vous avez passé du temps à réfléchir au problème et aux concepts qui l'entourent, donc certaines choses vous paraissent évidentes alors qu'elles ne le sont pas pour quelqu'un qui vient juste de lire l'énoncé. Vous devez donc écrire tout ce qui aidera votre ami à mieux comprendre votre solution. Pensez à tout ce que vous auriez aimé qu'on vous explique et qu'on vous détaille lorsque vous avez découvert le problème, quand vous n'aviez aucune idée de comment le résoudre.
Appliquez ce conseil même lorsque vous savez que la personne qui va réellement lire votre preuve connaît déjà le résultat et sait comment il se prouve. Par exemple, sur Mathraining, les correcteurs savent déjà que les énoncés sont corrects et ont eux-mêmes écrit une solution au problème par le passé. Mais vous ne devez pas écrire votre solution pour convaincre le correcteur : vous devez l'écrire pour convaincre toute personne qui verrait le problème et votre solution pour la première fois. Les étudiants commettent souvent l'erreur de se dire que les correcteurs savent déjà ce dont on parle et ce qu'on cherche à faire, et se permettent de ne donner quasi aucune explication, mais ce n'est pas cela qui est attendu de vous. (Il est d'ailleurs toujours possible que l'approche que vous aurez choisie pour résoudre un problème soit très différente de celle utilisée par les autres étudiants).
Rédigez ensuite chaque étape dans un paragraphe différent, de façon à ce que le lecteur puisse clairement identifier la structure de votre solution. Si vous avez beaucoup d'étapes, vous pouvez même penser à les numéroter. De cette façon vous pourrez plus facilement faire référence à un résultat ou un argument donné précédemment dans votre preuve. À chaque étape, mettez en évidence le ou les résultats intermédiaires importants qui vous seront utiles par la suite. Le lecteur ne va probablement pas faire l'effort de retenir par coeur l'entièreté de vos arguments et de vos égalités intermédiaires : c'est pourquoi vous devez l'aider un maximum en identifiant ce qu'il est important de retenir de chaque paragraphe.
Pour une solution plutôt longue, pensez à écrire une conclusion et/ou une introduction pour résumer ce que vous avez fait ou présenter ce que vous allez faire.
Sur Mathraining, une fois un problème résolu, vous aurez aussi la possibilité de lire les solutions d'autres élèves à ce problème, en particulier les solutions étoilées. Ces solutions sont mises en évidence car elles présentent différentes façons d'aborder le problème, mais aussi parce qu'elles sont bien rédigées. Si les correcteurs vous reprochent de ne pas avoir une bonne rédaction, alors pensez à regarder les solutions étoilées et à voir ce qui les différencie de votre solution pour comprendre les points sur lesquels vous pourriez vous améliorer.
Votre ami imaginaire
Rappelons tout d'abord qu'une preuve est un raisonnement par lequel on établit qu'une proposition est vraie. Pour qu'une preuve soit bonne, il est nécessaire que n'importe qui (ayant les prérequis mathématiques nécessaires) puisse la comprendre sans avoir aucun doute sur sa véracité. Il s'agit donc d'enchaîner des arguments les uns à la suite des autres, chaque argument devant être communément accepté comme évident.Pour savoir si la preuve que vous écrivez est bonne, vous pouvez essayer de vous mettre à la place de quelqu'un ayant les mêmes connaissances mathématiques que vous et qui découvrirait votre preuve pour la première fois. Cette personne fictive vient de découvrir le résultat que vous cherchez à démontrer, n'a même aucune idée de si ce résultat est vrai ou non, et la preuve qu'il s'apprête à lire doit le convaincre à $100\%$ que ce résultat est bien vrai. Cette personne est d'un naturel sceptique et tient à ce que tout soit très clairement justifié pour être pleinement convaincue. Elle est aussi pressée et ne tient pas à devoir réfléchir trois minutes à chaque argument pour comprendre comment il s'applique. Il faut donc que tout coule de source !
Notez bien que votre ami imaginaire ne lit pas dans vos pensées ! De votre côté, vous avez passé du temps à réfléchir au problème et aux concepts qui l'entourent, donc certaines choses vous paraissent évidentes alors qu'elles ne le sont pas pour quelqu'un qui vient juste de lire l'énoncé. Vous devez donc écrire tout ce qui aidera votre ami à mieux comprendre votre solution. Pensez à tout ce que vous auriez aimé qu'on vous explique et qu'on vous détaille lorsque vous avez découvert le problème, quand vous n'aviez aucune idée de comment le résoudre.
Appliquez ce conseil même lorsque vous savez que la personne qui va réellement lire votre preuve connaît déjà le résultat et sait comment il se prouve. Par exemple, sur Mathraining, les correcteurs savent déjà que les énoncés sont corrects et ont eux-mêmes écrit une solution au problème par le passé. Mais vous ne devez pas écrire votre solution pour convaincre le correcteur : vous devez l'écrire pour convaincre toute personne qui verrait le problème et votre solution pour la première fois. Les étudiants commettent souvent l'erreur de se dire que les correcteurs savent déjà ce dont on parle et ce qu'on cherche à faire, et se permettent de ne donner quasi aucune explication, mais ce n'est pas cela qui est attendu de vous. (Il est d'ailleurs toujours possible que l'approche que vous aurez choisie pour résoudre un problème soit très différente de celle utilisée par les autres étudiants).
Bien structurer votre solution
Avant de rédiger votre solution, il faut qu'elle soit la plus claire possible dans votre esprit. Vous devriez idéalement faire un plan de celle-ci, en énumérant les grandes étapes qui la constituent. Si vous ne le faites pas sur papier, passez au moins quelques secondes à réfléchir aux étapes clefs de votre solution et à l'ordre dans lequel vous allez les présenter lors de votre rédaction. Choisissez l'ordre qui vous semble le plus intuitif.Rédigez ensuite chaque étape dans un paragraphe différent, de façon à ce que le lecteur puisse clairement identifier la structure de votre solution. Si vous avez beaucoup d'étapes, vous pouvez même penser à les numéroter. De cette façon vous pourrez plus facilement faire référence à un résultat ou un argument donné précédemment dans votre preuve. À chaque étape, mettez en évidence le ou les résultats intermédiaires importants qui vous seront utiles par la suite. Le lecteur ne va probablement pas faire l'effort de retenir par coeur l'entièreté de vos arguments et de vos égalités intermédiaires : c'est pourquoi vous devez l'aider un maximum en identifiant ce qu'il est important de retenir de chaque paragraphe.
Pour une solution plutôt longue, pensez à écrire une conclusion et/ou une introduction pour résumer ce que vous avez fait ou présenter ce que vous allez faire.
Relisez-vous !
Probablement le point le plus important : lorsque vous avez terminé d'écrire votre solution, relisez-là ! Bien entendu pour corriger les éventuelles fautes de frappe, mais surtout pour vérifier que vous n'avez rien oublié et que tous les arguments s'enchaînent sans problème. Lorsque vous débutez, une bonne idée est même de laisser votre solution reposer une journée et de venir la relire le lendemain, avec un regard neuf. Vous aurez alors oublié tout ce que vous aviez en tête au moment d'écrire votre solution, et votre état d'esprit sera beaucoup plus proche de celui d'un correcteur qui découvrirait votre solution. Vous serez donc plus à-même de repérer les étapes insuffisamment justifiées ou qui ne sont pas faciles à comprendre.Sur Mathraining, une fois un problème résolu, vous aurez aussi la possibilité de lire les solutions d'autres élèves à ce problème, en particulier les solutions étoilées. Ces solutions sont mises en évidence car elles présentent différentes façons d'aborder le problème, mais aussi parce qu'elles sont bien rédigées. Si les correcteurs vous reprochent de ne pas avoir une bonne rédaction, alors pensez à regarder les solutions étoilées et à voir ce qui les différencie de votre solution pour comprendre les points sur lesquels vous pourriez vous améliorer.
2. Exemple algébrique
Une preuve, aussi mathématique soit elle, est avant tout un texte qui doit idéalement pouvoir être lu comme un roman. Lorsqu'on rédige une démonstration, on est évidemment vite amené à devoir écrire des équations (ou d'autres formules mathématiques). Pour autant, toutes ces parties plus mathématiques doivent être entourées d'un texte clair expliquant le contexte dans lequel on se trouve, ce que chaque équation signifie, comment plusieurs équations s'enchainent entre elles, etc.
Afin d'illustrer cela, regardons le problème suivant et quelques exemples de solutions.
Cette solution ne contient que des équations : absolument aucun texte ni même aucun symbole entre les équations pour expliquer ce qui les relie ! Certains passages, par exemple celui de la première à la deuxième ligne, sont relativement clairs, mais même dans ce cas-là il est important de relier les deux lignes au moins par un $\Leftrightarrow$ pour indiquer qu'elles sont équivalentes. Certains étudiants vont alors plutôt écrire la solution suivante :
"On m'a demandé de mettre des liens entre mes différentes lignes donc j'écris des $\Leftrightarrow$ partout et c'est gagné". Attention ! Le symbole $\Leftrightarrow$ a une signification exacte, ce n'est pas juste un signe de ponctuation ! Il signifie "si et seulement si" et ne peut dès lors être utilisé qu'entre deux équations qui sont strictement équivalentes.
La première et la deuxième ligne de notre solution sont bien équivalentes, car on a juste passé certains termes de droite à gauche. Par contre, il n'y a pas d'équivalence entre la deuxième et la troisième ligne ! Si la troisième ligne est vraie alors la deuxième ligne le sera aussi, car $28 \geq a + 4b + 9c$, mais le contraire est faux : il se pourrait très bien que la deuxième ligne soit vraie alors que la troisième est fausse. On pourrait donc théoriquement écrire $\Leftarrow$ à la place de $\Leftrightarrow$ entre ces deux lignes, mais en pratique on ne le fait presque jamais. On préférera plutôt écrire du texte en français pour expliquer le passage en question.
Par ailleurs, certains passages de cette solution sont loin d'être évidents, notamment le passage de la deuxième à la troisième ligne dont on vient de parler. Il faut absolument apporter des explications supplémentaires ici, car aucun lecteur découvrant cette solution pour la première fois ne va comprendre pourquoi $28$ peut être soudainement remplacé par $a+4b+9c$. La conclusion n'est pas claire du tout non plus : pourquoi la dernière inégalité est-elle toujours vraie ?
Cette troisième solution est parfaite : les $\Leftrightarrow$ ne sont utilisés qu'entre deux lignes strictement équivalentes et des explications sont apportées à chaque passage délicat.
Nous montrons un dernier exemple de solution à ce problème, que certains pourraient être tentés d'écrire mais que nous déconseillons fortement :
Cette solution est bien rigoureuse : elle utilise $\Rightarrow$ au lieu de $\Leftrightarrow$ au bon endroit, et elle donne des explications (relativement brèves) aux passages clefs. Par contre, en inversant ainsi l'ordre des inégalités pour partir de quelque chose de vrai et arriver à l'inégalité voulue, on a totalement perdu l'intuition ! De notre côté c'est la quatrième solution que l'on voit à ce problème, donc tout nous paraît très clair, mais n'oublions pas de nous mettre dans la peau de quelqu'un qui découvrirait cette solution-ci pour la première fois.
La première ligne $a(a-1)^2 + b(b-2)^2 + c(c-3)^2 > 0$ est certes vraie mais elle sort complètement de nulle part, avec a priori aucun rapport avec l'énoncé du problème. Un nouveau lecteur se poserait certainement la question de savoir s'il s'agit d'une réécriture de l'inégalité de l'énoncé, avant de finalement comprendre que la solution a été écrite "à l'envers". Cela peut être amusant de vouloir surprendre le lecteur en transformant une inégalité vraie jusqu'à tomber sur l'inégalité de l'énoncé, mais en général il vaut mieux essayer de garder le lecteur "avec soi", c'est-à-dire qu'il comprenne tout le long de la solution ce qu'on est en train de faire, pourquoi on est en train de le faire et où on veut arriver.
Afin d'illustrer cela, regardons le problème suivant et quelques exemples de solutions.
Problème
Montrer que $a^3 + b^3 + c^3 + 28 > 2a^2 + 4b^2 + 6c^2$ pour tous réels $0 < a, b, c \leq 2$.
Solution 1 (mauvaise)
$$a^3 + b^3 + c^3 + 28 > 2a^2 + 4b^2 + 6c^2$$ $$a^3 - 2a^2 + b^3 - 4b^2 + c^3 - 6c^2 + 28 > 0$$ $$a^3 - 2a^2 + b^3 - 4b^2 + c^3 - 6c^2 + a + 4b + 9c > 0$$ $$a(a^2 - 2a + 1) + b(b^2-4b+4) + c(c^2-6c+9) > 0$$ $$a(a-1)^2 + b(b-2)^2 + c(c-3)^2 > 0$$
Cette solution ne contient que des équations : absolument aucun texte ni même aucun symbole entre les équations pour expliquer ce qui les relie ! Certains passages, par exemple celui de la première à la deuxième ligne, sont relativement clairs, mais même dans ce cas-là il est important de relier les deux lignes au moins par un $\Leftrightarrow$ pour indiquer qu'elles sont équivalentes. Certains étudiants vont alors plutôt écrire la solution suivante :
Solution 2 (mauvaise)
$$\begin{align}
& a^3 + b^3 + c^3 + 28 > 2a^2 + 4b^2 + 6c^2 \\
\Leftrightarrow\ & a^3 - 2a^2 + b^3 - 4b^2 + c^3 - 6c^2 + 28 > 0 \\
\Leftrightarrow\ & a^3 - 2a^2 + b^3 - 4b^2 + c^3 - 6c^2 + a + 4b + 9c > 0 \\
\Leftrightarrow\ & a(a^2 - 2a + 1) + b(b^2-4b+4) + c(c^2-6c+9) > 0 \\
\Leftrightarrow\ & a(a-1)^2 + b(b-2)^2 + c(c-3)^2 > 0 \\
\end{align}$$
& a^3 + b^3 + c^3 + 28 > 2a^2 + 4b^2 + 6c^2 \\
\Leftrightarrow\ & a^3 - 2a^2 + b^3 - 4b^2 + c^3 - 6c^2 + 28 > 0 \\
\Leftrightarrow\ & a^3 - 2a^2 + b^3 - 4b^2 + c^3 - 6c^2 + a + 4b + 9c > 0 \\
\Leftrightarrow\ & a(a^2 - 2a + 1) + b(b^2-4b+4) + c(c^2-6c+9) > 0 \\
\Leftrightarrow\ & a(a-1)^2 + b(b-2)^2 + c(c-3)^2 > 0 \\
\end{align}$$
"On m'a demandé de mettre des liens entre mes différentes lignes donc j'écris des $\Leftrightarrow$ partout et c'est gagné". Attention ! Le symbole $\Leftrightarrow$ a une signification exacte, ce n'est pas juste un signe de ponctuation ! Il signifie "si et seulement si" et ne peut dès lors être utilisé qu'entre deux équations qui sont strictement équivalentes.
La première et la deuxième ligne de notre solution sont bien équivalentes, car on a juste passé certains termes de droite à gauche. Par contre, il n'y a pas d'équivalence entre la deuxième et la troisième ligne ! Si la troisième ligne est vraie alors la deuxième ligne le sera aussi, car $28 \geq a + 4b + 9c$, mais le contraire est faux : il se pourrait très bien que la deuxième ligne soit vraie alors que la troisième est fausse. On pourrait donc théoriquement écrire $\Leftarrow$ à la place de $\Leftrightarrow$ entre ces deux lignes, mais en pratique on ne le fait presque jamais. On préférera plutôt écrire du texte en français pour expliquer le passage en question.
Par ailleurs, certains passages de cette solution sont loin d'être évidents, notamment le passage de la deuxième à la troisième ligne dont on vient de parler. Il faut absolument apporter des explications supplémentaires ici, car aucun lecteur découvrant cette solution pour la première fois ne va comprendre pourquoi $28$ peut être soudainement remplacé par $a+4b+9c$. La conclusion n'est pas claire du tout non plus : pourquoi la dernière inégalité est-elle toujours vraie ?
Solution 3 (bonne)
Nous cherchons à montrer que
$$\begin{align}
& a^3 + b^3 + c^3 + 28 > 2a^2 + 4b^2 + 6c^2\\
\Leftrightarrow\ & a^3 - 2a^2 + b^3 - 4b^2 + c^3 - 6c^2 + 28 > 0\\
\end{align}$$ Vu que $a, b, c \leq 2$, on a $a+4b+9c \leq 2 + 8 + 18 = 28$ et donc il suffit de montrer que
$$\begin{align}
&a^3 - 2a^2 + b^3 - 4b^2 + c^3 - 6c^2 + a + 4b + 9c > 0\\
\Leftrightarrow\ & a(a^2 - 2a + 1) + b(b^2-4b+4) + c(c^2-6c+9) > 0\\
\Leftrightarrow\ & a(a-1)^2 + b(b-2)^2 + c(c-3)^2 > 0\\
\end{align}$$ Cette dernière inégalité est bien vraie. En effet, vu que $a, b, c > 0$, et comme un carré est toujours positif, le membre de gauche est toujours positif. Par ailleurs, il est même toujours strictement positif car le terme $c(c-3)^2$ est strictement positif : on a $c > 0$ par hypothèse et $(c-3)^2 > 0$ car $c \neq 3$.
$$\begin{align}
& a^3 + b^3 + c^3 + 28 > 2a^2 + 4b^2 + 6c^2\\
\Leftrightarrow\ & a^3 - 2a^2 + b^3 - 4b^2 + c^3 - 6c^2 + 28 > 0\\
\end{align}$$ Vu que $a, b, c \leq 2$, on a $a+4b+9c \leq 2 + 8 + 18 = 28$ et donc il suffit de montrer que
$$\begin{align}
&a^3 - 2a^2 + b^3 - 4b^2 + c^3 - 6c^2 + a + 4b + 9c > 0\\
\Leftrightarrow\ & a(a^2 - 2a + 1) + b(b^2-4b+4) + c(c^2-6c+9) > 0\\
\Leftrightarrow\ & a(a-1)^2 + b(b-2)^2 + c(c-3)^2 > 0\\
\end{align}$$ Cette dernière inégalité est bien vraie. En effet, vu que $a, b, c > 0$, et comme un carré est toujours positif, le membre de gauche est toujours positif. Par ailleurs, il est même toujours strictement positif car le terme $c(c-3)^2$ est strictement positif : on a $c > 0$ par hypothèse et $(c-3)^2 > 0$ car $c \neq 3$.
Cette troisième solution est parfaite : les $\Leftrightarrow$ ne sont utilisés qu'entre deux lignes strictement équivalentes et des explications sont apportées à chaque passage délicat.
Nous montrons un dernier exemple de solution à ce problème, que certains pourraient être tentés d'écrire mais que nous déconseillons fortement :
Solution 4 (bonne mais déconseillée)
$$\begin{array}{lll}
& a(a-1)^2 + b(b-2)^2 + c(c-3)^2 > 0 & \text{ car $a, b, c > 0$ et $c \neq 3$}\\
\Leftrightarrow & a(a^2 - 2a + 1) + b(b^2-4b+4) + c(c^2-6c+9) > 0& \\
\Leftrightarrow & a^3 - 2a^2 + b^3 - 4b^2 + c^3 - 6c^2 + a + 4b + 9c > 0& \\
\Rightarrow & a^3 - 2a^2 + b^3 - 4b^2 + c^3 - 6c^2 + 28 > 0 & \text{ car $28 \geq a+4b+9c$, car $a, b, c \leq 2$}\\
\Leftrightarrow & a^3 + b^3 + c^3 + 28 > 2a^2 + 4b^2 + 6c^2& \\
\end{array}$$
& a(a-1)^2 + b(b-2)^2 + c(c-3)^2 > 0 & \text{ car $a, b, c > 0$ et $c \neq 3$}\\
\Leftrightarrow & a(a^2 - 2a + 1) + b(b^2-4b+4) + c(c^2-6c+9) > 0& \\
\Leftrightarrow & a^3 - 2a^2 + b^3 - 4b^2 + c^3 - 6c^2 + a + 4b + 9c > 0& \\
\Rightarrow & a^3 - 2a^2 + b^3 - 4b^2 + c^3 - 6c^2 + 28 > 0 & \text{ car $28 \geq a+4b+9c$, car $a, b, c \leq 2$}\\
\Leftrightarrow & a^3 + b^3 + c^3 + 28 > 2a^2 + 4b^2 + 6c^2& \\
\end{array}$$
Cette solution est bien rigoureuse : elle utilise $\Rightarrow$ au lieu de $\Leftrightarrow$ au bon endroit, et elle donne des explications (relativement brèves) aux passages clefs. Par contre, en inversant ainsi l'ordre des inégalités pour partir de quelque chose de vrai et arriver à l'inégalité voulue, on a totalement perdu l'intuition ! De notre côté c'est la quatrième solution que l'on voit à ce problème, donc tout nous paraît très clair, mais n'oublions pas de nous mettre dans la peau de quelqu'un qui découvrirait cette solution-ci pour la première fois.
La première ligne $a(a-1)^2 + b(b-2)^2 + c(c-3)^2 > 0$ est certes vraie mais elle sort complètement de nulle part, avec a priori aucun rapport avec l'énoncé du problème. Un nouveau lecteur se poserait certainement la question de savoir s'il s'agit d'une réécriture de l'inégalité de l'énoncé, avant de finalement comprendre que la solution a été écrite "à l'envers". Cela peut être amusant de vouloir surprendre le lecteur en transformant une inégalité vraie jusqu'à tomber sur l'inégalité de l'énoncé, mais en général il vaut mieux essayer de garder le lecteur "avec soi", c'est-à-dire qu'il comprenne tout le long de la solution ce qu'on est en train de faire, pourquoi on est en train de le faire et où on veut arriver.
3. Exemple géométrique
Regardons à présent un problème de géométrie et une solution à celui-ci. Les étapes de la solution sont relativement élémentaires, mais il est possible que vous n'ayez pas encore vu toute la théorie utilisée. Ce n'est pas grave : le principal est surtout de lire les conseils sur la rédaction de la solution.
Il y a plein de choses à redire sur cette solution :
La solution suivante prend en compte toutes ces remarques, ce qui rend la solution bien plus facile et agréable à lire. Remarquez comme la solution est aérée. Même si elle parait plus longue que la solution précédente, elle est en fait beaucoup plus rapide à lire et à comprendre.
Problème
Soit $ABC$ un triangle et $\ell$ la tangente en $A$ au cercle circonscrit à $ABC$. Le cercle passant par $A$ et tangent à $BC$ en $B$ (respectivement $C$) coupe $\ell$ en $A$ et $C'$ (respectivement $B'$). Montrer que
$$\frac{|B'C|}{|AB|} + \frac{|C'B|}{|AC|} \ge 2$$
$$\frac{|B'C|}{|AB|} + \frac{|C'B|}{|AC|} \ge 2$$
Solution 1 (mauvaise)
On trouve que $\widehat{ACB} = \widehat{C'AB} = \widehat{AB'C}$ et $\widehat{ABC} = \widehat{B'AC} = \widehat{AC'B}$ par chasse aux angles, donc les triangles $ABC'$ et $ACB'$ sont semblables. Donc $\frac{|C'B|}{|AC|} = \frac{|AB|}{|B'C|}$. Donc $\frac{\frac{|B'C|}{|AB|} + \frac{|C'B|}{|AC|}}{2} \ge \sqrt{\frac{|B'C|}{|AB|} \cdot \frac{|C'B|}{|AC|}} = 1$ par AM-GM, donc $\frac{|B'C|}{|AB|} + \frac{|C'B|}{|AC|} \ge 2$.
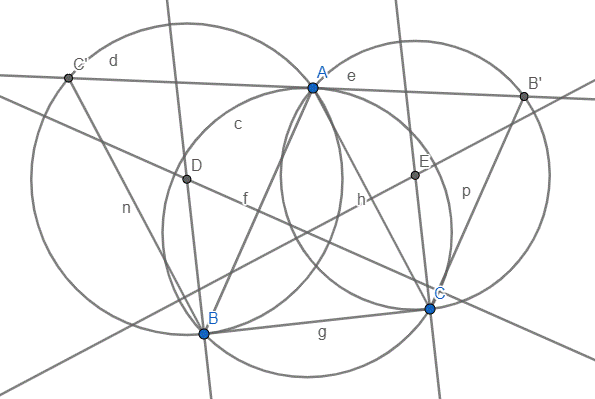

Il y a plein de choses à redire sur cette solution :
- C'est très bien d'inclure une figure pour un problème de géométrie. Par contre, il faut que cette figure soit lisible ! Ici, la personne écrivant cette solution a laissé sur la figure des droites qu'il a utilisées pour la construire, alors qu'elles sont parfaitement inutiles pour la solution. Il a également laissé les étiquettes de toutes les droites, et il n'a pas fait l'effort de bouger les noms des points intéressants pour les rendre plus faciles à lire. Il est donc presque impossible de se servir de cette figure pour suivre la solution... Une bonne figure devrait aussi mettre en évidence, si possible avec des couleurs, les angles de même amplitude révélés par la chasse aux angles. Un exemple de bonne figure est donné plus bas.
- La chasse aux angles n'est pas détaillée du tout, et c'est ici au lecteur de se demander comment chaque égalité a été obtenue, ce qui n'est pas évident. Ce qui complexifie encore plus la compréhension, c'est le fait que les égalités d'angles ne sont pas écrites dans le bon ordre ! Ici, les égalités $\widehat{C'AB} = \widehat{ACB}$ et $\widehat{ACB} = \widehat{AB'C}$ sont les égalités que l'on connaît, et on veut en déduire que $\widehat{C'AB} = \widehat{AB'C}$. Dans ce cas, il faut absolument écrire
$$\widehat{C'AB} = \widehat{ACB} = \widehat{AB'C}$$ pour que chaque signe $=$ corresponde à une égalité connue et que l'égalité démontrée soit celle entre le premier et le dernier terme. Le lecteur lit de gauche à droite, et quand il lit
$$\widehat{ACB} = \widehat{C'AB} = \widehat{AB'C}$$ c'est impossible pour lui de deviner que le $= \widehat{AB'C}$ est obtenu à partir de $\widehat{ACB}$ et non $\widehat{C'AB}$ ! Ce conseil n'est pas valable que pour la géométrie : dans n'importe quel contexte, lorsqu'on écrit une égalité du type $W = X = Y = Z$, il faut que les égalités $W = X$, $X = Y$ et $Y = Z$ soient les égalités évidentes et que l'égalité $W = Z$ soit celle que l'on cherche à montrer. - Lorsqu'on donne des triangles semblables, il faut faire l'effort de lister les sommets de ces triangles dans le bon ordre. Ici il faut donc dire que $ABC'$ et $B'CA$ (et non $ACB'$) sont semblables. De cette manière, on peut directement vérifier l'égalité $\dfrac{|C'B|}{|AC|} = \dfrac{|AB|}{|B'C|}$ sans même se référer à la figure.
- L'inégalité qui est écrite est presque illisible : il faut faire en sorte de la rendre plus lisible, par exemple en la centrant (avec des doubles dollars en $\LaTeX$). Idéalement on mettra chaque (in)égalité importante en évidence au centre pour faciliter la lecture.
- Cela relève un peu plus de l'esthétique, mais l'étudiant utilise quatre fois "donc" dans cette solution de deux phrases. Il existe plein de façons de passer d'une affirmation à une autre, et on essayera en général d'utiliser différentes formulations pour rendre la solution moins rébarbative.
La solution suivante prend en compte toutes ces remarques, ce qui rend la solution bien plus facile et agréable à lire. Remarquez comme la solution est aérée. Même si elle parait plus longue que la solution précédente, elle est en fait beaucoup plus rapide à lire et à comprendre.
Solution 2 (bonne)
Notons $\Omega$ le cercle circonscrit à $ABC$, et $\Omega_B$ (respectivement $\Omega_C$) le cercle passant par $A$ et tangent à $BC$ en $B$ (respectivement $C$).
Par chasse aux angles, on trouve que $$\widehat{C'AB} = \widehat{ACB} = \widehat{AB'C},$$ par égalité d'angles tangentiel et inscrit dans $\Omega$ puis dans $\Omega_C$. De la même manière, on obtient que
$$\widehat{B'AC} = \widehat{ABC} = \widehat{AC'B}$$ par égalités d'angles tangentiel et inscrit dans $\Omega$ puis dans $\Omega_B$.
Les triangles $ABC'$ et $B'CA$ sont donc semblables, puisqu'ils ont deux paires d'angles en commun. En particulier, il vient que
$$\frac{|C'B|}{|AC|} = \frac{|AB|}{|B'C|}.$$ Par inégalité des moyennes arithmétique et géométrique, on déduit que
$$\frac 1 2 \cdot \left(\frac{|B'C|}{|AB|} + \frac{|C'B|}{|AC|}\right) \ge \sqrt{\frac{|B'C|}{|AB|} \cdot \frac{|C'B|}{|AC|}} = 1,$$ ce qui implique bien que
$$\frac{|B'C|}{|AB|} + \frac{|C'B|}{|AC|} \ge 2.$$
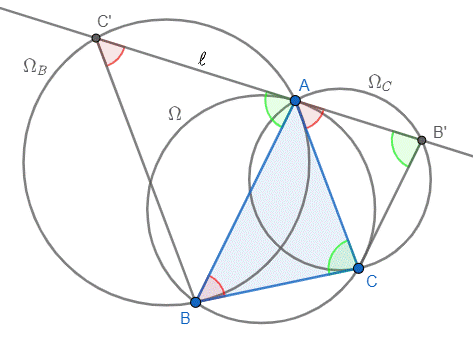
Par chasse aux angles, on trouve que $$\widehat{C'AB} = \widehat{ACB} = \widehat{AB'C},$$ par égalité d'angles tangentiel et inscrit dans $\Omega$ puis dans $\Omega_C$. De la même manière, on obtient que
$$\widehat{B'AC} = \widehat{ABC} = \widehat{AC'B}$$ par égalités d'angles tangentiel et inscrit dans $\Omega$ puis dans $\Omega_B$.
Les triangles $ABC'$ et $B'CA$ sont donc semblables, puisqu'ils ont deux paires d'angles en commun. En particulier, il vient que
$$\frac{|C'B|}{|AC|} = \frac{|AB|}{|B'C|}.$$ Par inégalité des moyennes arithmétique et géométrique, on déduit que
$$\frac 1 2 \cdot \left(\frac{|B'C|}{|AB|} + \frac{|C'B|}{|AC|}\right) \ge \sqrt{\frac{|B'C|}{|AB|} \cdot \frac{|C'B|}{|AC|}} = 1,$$ ce qui implique bien que
$$\frac{|B'C|}{|AB|} + \frac{|C'B|}{|AC|} \ge 2.$$

4. Exemple combinatoire
Voici un troisième problème ainsi qu'une solution mal rédigée à celui-ci. À nouveau, notre but est de montrer tout ce qui peut être amélioré dans cette solution.
Beaucoup de critiques peuvent être émises quant à cette solution :
Voici une meilleure solution prenant en compte toutes ces remarques.
Problème
On dit que deux nombres à trois chiffres sont similaires s'ils ont au moins deux chiffres en commun, à la même position. Par exemple, les nombres $284$ et $204$ sont similaires, mais les nombres $379$ et $973$ ne le sont pas. Quelle est, au maximum, la taille d'un sous-ensemble de $S = \{100, 101, \ldots, 999\}$ ne contenant aucune paire de nombres similaires ?
Solution 1 (mauvaise)
Prenons les $90$ nombres $100, 111, 122, \ldots, 199, 201, 212, \ldots, 290, \ldots, 908, 919, \ldots, 997$. Ces nombres ne sont pas similaires car si ils ont le même chiffre des centaines alors ils n'ont pas le même chiffre des dizaines et pas le même chiffre des unités et s'ils n'ont pas le même chiffre des centaines alors ils n'ont pas à la fois le même chiffre des dizaines et le même chiffre des unités car on a décalé le chiffre des unités par rapport au chiffre des dizaines à chaque nouvelle centaine. Si on prend $91$ nombres au lieu de $90$ alors le dernier nombre devra forcément avoir le même chiffre des centaines que $10$ autres nombres et ce nombre sera forcément similaire à l'un des $10$ nombres car tous les chiffres des dizaines sont déjà pris.
Beaucoup de critiques peuvent être émises quant à cette solution :
- La liste des $90$ nombres n'est pas du tout évidente à comprendre. C'est un exemple typique où l'élève sait parfaitement ce qu'il veut dire vu qu'il a réfléchi à la construction de ces nombres pendant longtemps, mais un lecteur qui n'est pas dans sa tête ne va pas facilement comprendre comment compléter les petits points de la liste, ni ce qui a amené l'étudiant à considérer ce sous-ensemble assez particulier. Il n'est en fait même pas clair qu'il y a exactement $90$ nombres dans ce sous-ensemble. L'élève devrait réfléchir à une meilleure manière de présenter ces nombres, pour donner une meilleure intuition de ce qu'il est en train de faire. Une façon de le faire consiste à donner une formule explicite : il s'agit ici des nombres $\overline{abc}$ avec $c = a+b-1$ (ou $a+b-11$ si $a+b \ge 11$).
- La deuxième phrase de cette solution est beaucoup trop longue, sans aucun signe de ponctuation, ce qui la rend quasi incompréhensible ! Il faut absolument découper une telle phrase à rallonge en plusieurs morceaux, sans quoi personne ne va avoir le courage de poursuivre la lecture de cette solution. Par ailleurs, cette phrase est très peu rigoureuse pour prouver qu'il n'y a pas deux nombres similaires parmi les $90$ qui ont été donnés. L'élève explique à peu près comment il a essayé d'éviter d'avoir deux nombres similaires lors de la construction de ses $90$ nombres, mais il ne donne pas de justification suffisamment claire au fait que ça fonctionne. C'est en fait une conséquence de la première remarque : les nombres n'ont pas été décrits de manière très explicite donc il est difficile d'apporter une preuve rigoureuse au fait que ces nombres vérifient une certaine propriété.
- Sur base de ces deux premières remarques, on peut essayer de formaliser la preuve. Nous avons vu plus haut que les $90$ nombres sont ceux de la forme $\overline{abc}$ avec $c = a+b-1$ (ou $a+b-11$ si $a+b \ge 11$). Une erreur classique consiste, lorsqu'on pense avoir trouvé une solution à un problème, à foncer tête baissée dans sa rédaction sans se demander si elle ne pourrait pas être légèrement modifiée pour la rendre plus courte ou plus facile à rédiger. Ici, notre formule $c = a+b-1$ ou $a+b-11$ n'est pas très jolie, et elle risque d'être pénible à utiliser pour nous justifier. Après un peu de réflexion, on peut voir qu'une façon d'éviter ce "ou" est de dire que $a+b-1-c$ doit être divisible par $10$. C'est déjà plus joli, mais continuons à prendre un peu de recul. Cette expression $a+b-1-c$ est un peu bizarre, avec ce $-1$ et ce $c$ précédé d'un signe $-$ alors que $a$ et $b$ sont précédés d'un $+$. Ne pourrait-on pas modifier cette expression, quitte à modifier légèrement la liste des $90$ nombres ? Que se passe-t-il si on prend les nombres $\overline{abc}$ tels que $a+b+c$ est divisible par $10$ ? Cela marche aussi ! Et voilà, on a trouvé un sous-ensemble de $90$ nombres beaucoup plus facile à décrire, et cela va grandement simplifier la rédaction d'une preuve rigoureuse au fait qu'il n'y a pas deux nombres similaires parmi ceux-ci. C'est fait dans la solution ci-dessous.
- La dernière phrase, pour montrer que $91$ ne fonctionne pas, est également très mal écrite. Même si l'idée est là, l'étudiant semble justifier les choses en rajoutant un $91^\text{ème}$ nombre aux $90$ déjà choisis. C'est une erreur commune : on ne peut pas supposer que les $90$ premiers nombres sont d'une forme particulière pour prouver que ça ne fonctionnera pas avec $91$ nombres ! Pour rendre cette preuve rigoureuse, il faut trouver une manière plus générale de présenter les choses. Le principe des tiroirs, comme souvent, peut ici nous aider.
- Il n'y a aucune conclusion dans cette solution : l'étudiant ne répond même pas explicitement à la question qu'on lui pose ! Dans un tel problème où on demande de trouver le plus grand nombre vérifiant une propriété, une bonne façon de rédiger sa solution consiste à commencer par donner la réponse numérique et expliquer la stratégie que l'on va adopter pour la prouver. Lorsque la preuve se découpe en plusieurs parties comme ici (montrer que $90$ fonctionne puis que $91$ ne fonctionne pas), il est aussi naturel de scinder la preuve en plusieurs paragraphes.
Voici une meilleure solution prenant en compte toutes ces remarques.
Solution 2 (bonne)
Nous allons montrer que la réponse est $90$, en montrant d'abord qu'il existe un sous-ensemble de $S$ à $90$ éléments ne contenant aucune paire de nombres similaires, puis en montrant qu'un sous-ensemble de $S$ avec au moins $91$ éléments contient forcément deux nombres similaires.
- Considérons le sous-ensemble $X$ de $S$ défini par
$$X = \left\{\overline{abc} \ : \ \begin{align}&1 \le a \le 9\\ &0 \le b, c \le 9\\ & 10 \mid a+b+c\end{align} \right\}$$ où $\overline{abc}$ est le nombre ayant $a, b, c$ pour chiffres dans le système décimal.
On a $|X| = 90$, puisque pour chaque chiffre $a \ne 0$ et chaque chiffre $b$, il y a exactement un chiffre $c$ tel que $a+b+c$ est multiple de $10$.
Montrons maintenant que deux nombres différents dans $X$ ne sont jamais similaires. Supposons par l'absurde qu'il existe deux nombres différents similaires $\overline{abc}$ et $\overline{def}$ dans $X$. Cela signifie qu'exactement deux des trois égalités $a = d$, $b = e$ et $c = f$ sont vérifiées. Cela implique en particulier que
$$a+b+c \ne d+e+f$$ et
$$|(a+b+c) - (d+e+f)| \le 9,$$ ce qui est impossible car $a+b+c$ et $d+e+f$ sont tous les deux multiples de $10$ par définition de $X$. - Considérons un sous-ensemble $Y$ de $S$ avec $|Y| \ge 91$ et montrons qu'il contient forcément deux nombres similaires. Définissons les $90$ sous-ensembles $S_{10}, S_{11}, \ldots, S_{99}$ de $S$ par
$$S_i = \left\{10\cdot i + j \mid 0 \le j \le 9 \right\} \text{ pour tout $i \in \{10, 11, \ldots, 99\}$}.$$ On a $S = S_{10} \cup S_{11} \cup \ldots \cup S_{99}$. Par le principe des tiroirs, il existe deux éléments de $Y$ se trouvant dans le même ensemble $S_i$. Ces deux nombres ont donc le même chiffre des centaines et le même chiffre des dizaines : ils sont similaires.
5. Exercice supplémentaire
L'exercice suivant faisait initialement partie des exercices de ce chapitre, mais il a été retiré car jugé trop subjectif par la communauté. Nous vous conseillons toutefois de réfléchir à chaque proposition avant de lire les réponses qui étaient attendues.
Voici un problème de théorie des nombres et une solution à ce problème.
Quels commentaires peut-on faire sur cette solution ?
Les réponses attendues étaient les suivantes :
Voici une meilleure solution qui aurait pu être donnée à ce problème :
Voici un problème de théorie des nombres et une solution à ce problème.
Problème
Combien y a-t-il de nombres premiers $p$ tels que $p^2+1$ est également un nombre premier ?
Solution
Si $p$ est impair, alors $p^2$ est aussi impair et $p^2+1$ est donc pair. Donc $p^2+1$ n'est pas premier (car $p \ne 1$). Donc $p$ est pair. Donc $p = 2$ car $p$ est premier.
Quels commentaires peut-on faire sur cette solution ?
- La solution est très courte et contient $4$ fois le mot "donc" : il serait préférable de varier les tournures de phrases pour rendre la solution plus agréable à lire.
- La solution contient $4$ phrases : il faudrait les séparer en $4$ paragraphes pour rendre la solution plus lisible.
- La justification "car $p \ne 1$" pour passer de $p^2+1$ pair à $p^2+1$ non premier est correcte mais fort raccourcie : ça vaudrait la peine de détailler ce passage.
- Le passage de $p^2+1$ non premier à $p$ pair mériterait d'être mieux expliqué car il faut se rappeler que l'énoncé demande $p^2+1$ premier et qu'on a supposé $p$ impair au début de la solution.
- En dehors de la rédaction qui n'est pas idéale, la solution montre bien que $p = 2$ est l'unique nombre vérifiant l'énoncé.
- La solution ne répond pas explicitement à la question de l'énoncé.
Les réponses attendues étaient les suivantes :
- Vrai. Même s'il n'est pas interdit d'utiliser "donc" à chaque phrase, cela rend la solution très monotone.
- Faux. Les paragraphes peuvent servir à mieux structurer sa solution. Un paragraphe est en général un groupe de plusieurs phrases qui forment ensemble une étape de la solution. Mettre une phrase par paragraphe n'améliorera pas du tout la compréhension.
- Vrai. Pour passer de $p^2+1$ pair à $p^2+1$ non premier, il faut remarquer que le seul nombre premier pair est $2$, que $p^2+1$ ne peut valoir $2$ que pour $p = 1$, et que $p$ ne peut pas valoir $1$ car il est supposé premier. Résumer tout cela en un simple "car $p \ne 1$" est assez violent, surtout pour un problème aussi simple. C'est sans doute très clair pour la personne ayant écrit cette solution, mais c'est beaucoup trop condensé pour le lecteur qui la découvre.
- Vrai. La solution enchaîne d'abord les implications directes, en ce sens que chaque affirmation implique directement la suivante. On a $p$ impair qui implique $p^2$ impair, puis $p^2$ impair qui implique $p^2+1$ pair, puis $p^2+1$ pair qui implique $p^2+1$ non premier. Lorsqu'on lit "Donc $p$ est pair" sans plus de justification, on pense naturellement qu'il s'agit à nouveau d'une implication directe, c'est-à-dire que cela vient directement de $p^2+1$ non premier. Or ce n'est pas le cas : ce "Donc" qui ressemble à tous les autres cache le fait que $p^2+1$ non premier rentre en contradiction avec l'énoncé et que notre hypothèse de départ ($p$ impair) était fausse ! La plupart des personnes lisant cette solution vont prendre du temps à comprendre ce passage : la personne ayant rédigé cette solution aurait du le rendre plus clair.
- Faux. Il manque une étape cruciale à la fin de cette solution : on a prouvé que si $p$ vérifie l'énoncé alors $p = 2$, mais on a aucunement regardé si $p = 2$ vérifie l'énoncé. C'est bien le cas car $2^2+1 = 5$ est premier, mais il fallait bien sûr le mentionner. (Note : Il s'agit ici d'une vraie erreur de raisonnement, et pas uniquement d'un problème de rédaction).
- Vrai. L'énoncé demande combien de nombres $p$ vérifient la propriété, donc il est important de répondre explicitement à la question en disant qu'il y a un seul tel nombre.
Voici une meilleure solution qui aurait pu être donnée à ce problème :
Solution (meilleure)
Supposons tout d'abord que $p$ est impair et vérifie l'énoncé. Dans ce cas, $p^2$ est aussi impair et $p^2+1$ est pair. Mais $p^2+1$ est supposé premier, et le seul nombre premier pair est $2$, d'où on déduit que $p^2+1 = 2$, c'est-à-dire $p = 1$. C'est impossible car $1$ n'est pas premier.
Supposons à présent que $p$ est pair et vérifie l'énoncé. Le seul nombre premier pair étant $2$, la seule option est $p = 2$. Vu que $2^2+1 = 5$ est premier, le nombre $p = 2$ vérifie bien l'énoncé.
Il y a donc un seul nombre premier $p$ tel que $p^2+1$ est premier : il s'agit de $p = 2$.
Supposons à présent que $p$ est pair et vérifie l'énoncé. Le seul nombre premier pair étant $2$, la seule option est $p = 2$. Vu que $2^2+1 = 5$ est premier, le nombre $p = 2$ vérifie bien l'énoncé.
Il y a donc un seul nombre premier $p$ tel que $p^2+1$ est premier : il s'agit de $p = 2$.