Théorie > Géométrie > Inversion et polarisation
Prérequis
Résumé
L'inversion est une transformation du plan particulière qui transforme les droites en cercles, et réciproquement. Il s'agit d'un outil très puissant qui permet parfois de venir facilement à bout de problèmes a priori fort compliqués. Nous nous en servons notamment pour montrer les deux implications du théorème de Ptolémée. La polarisation, quant à elle, est liée à l'inversion et associe à tout point du plan une droite (et réciproquement). Maîtriser les propriétés des polarisations peut également permettre de faciliter des preuves, comme nous l'illustrons dans ce chapitre sur deux exemples concrets.
Ce chapitre a été écrit par N. Radu et mis en ligne le 23 juillet 2016.
1. Inversion
Les inversions sont des transformations du plan très particulières, de par le fait qu'elles modifient complètement les objets présents sur la figure. Comme nous allons le voir, les inversions transforment certains cercles en droites, et c'est une des raisons pour lesquelles elles peuvent être très utiles. En effet, en présence d'une figure contenant beaucoup de cercles, il peut parfois se révéler utile d'appliquer une inversion pour transformer la plupart de ces cercles en droites, objets que l'on maîtrise généralement mieux. Aussi, comme pour les transformations du plan classiques, remarquer dans un problème que certains objets sont images de certains autres par une inversion particulière peut permettre de progresser dans sa résolution.
Étant donnés un point $O$ du plan et un réel $k > 0$, on définit l'inversion de centre $O$ et de rapport $k$ en disant que l'image d'un point $P$ différent de $O$ est l'unique point $P'$ appartenant à la demi-droite $[OP)$ et tel que $|OP| \cdot |OP'| = k$. De manière générale, on peut en fait aussi définir l'inversion de centre $O$ et de rapport $k$ lorsque $k < 0$. Celle-ci revient à effectuer l'inversion de centre $O$ et de rapport $|k|$ puis la symétrie centrale de centre $O$.
En général, lorsque l'on désire effectuer une inversion, on ne donne pas réellement la valeur de $k$. On précise plutôt l'image d'un point particulier. Par exemple, si l'on est en présence de trois points $O$, $A$ et $A'$ alignés, on peut parler de l'inversion de centre $O$ envoyant $A$ sur $A'$. Cela revient exactement à dire que l'on considère l'inversion de centre $O$ et de rapport $k = |OA| \cdot |OA'|$ (ou $-|OA| \cdot |OA'|$ si $A$ et $A'$ ne sont pas du même côté de $O$).
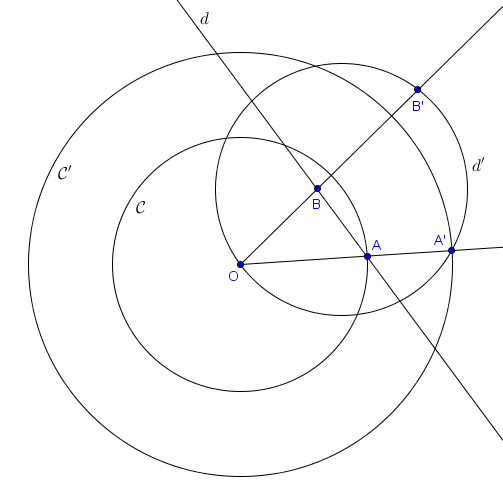
Il découle de la définition d'inversion que si un point $P$ a pour image $P'$ (par une certaine inversion), alors le point $P'$ a pour image $P$. Sur l'exemple ci-dessus, l'image de $A'$ par l'inversion est donc $A$, l'image de $\mathcal{C'}$ est $\mathcal{C}$, l'image de $B'$ est $B$, et l'image du cercle $d'$ est la droite $d$.
On a aussi la propriété suivante, dont la démonstration est une application directe de la définition d'inversion. La figure plus haut permet de mieux visualiser la propriété.
Définition
Intuitivement, une inversion de centre $O$ va être telle que les points éloignés de $O$ en deviendront proches, et vice versa.Étant donnés un point $O$ du plan et un réel $k > 0$, on définit l'inversion de centre $O$ et de rapport $k$ en disant que l'image d'un point $P$ différent de $O$ est l'unique point $P'$ appartenant à la demi-droite $[OP)$ et tel que $|OP| \cdot |OP'| = k$. De manière générale, on peut en fait aussi définir l'inversion de centre $O$ et de rapport $k$ lorsque $k < 0$. Celle-ci revient à effectuer l'inversion de centre $O$ et de rapport $|k|$ puis la symétrie centrale de centre $O$.
En général, lorsque l'on désire effectuer une inversion, on ne donne pas réellement la valeur de $k$. On précise plutôt l'image d'un point particulier. Par exemple, si l'on est en présence de trois points $O$, $A$ et $A'$ alignés, on peut parler de l'inversion de centre $O$ envoyant $A$ sur $A'$. Cela revient exactement à dire que l'on considère l'inversion de centre $O$ et de rapport $k = |OA| \cdot |OA'|$ (ou $-|OA| \cdot |OA'|$ si $A$ et $A'$ ne sont pas du même côté de $O$).
Exemple
Pour bien comprendre la notion d'inversion, observons un exemple. Sur la figure suivante, nous considérons l'inversion de centre $O$ envoyant $A$ sur $A'$. Le cercle $\mathcal{C}$ de centre $O$ et passant par $A$ est alors logiquement envoyé sur le cercle $\mathcal{C'}$ de centre $O$ et passant par $A'$. L'image du point $B$ par l'inversion est notée $B'$. Puisque $B$ se situe à l'intérieur de $\mathcal{C}$, on a $|OB| < |OA|$. Il découle alors de la définition que $B'$ doit vérifier $|OB'| > |OA'|$. C'est pourquoi $B'$ se situe à l'extérieur de $\mathcal{C'}$. Le plus intéressant, sur cet exemple, est le cas de la droite $d = AB$. On sait que l'image de cette droite doit passer par $A'$ et par $B'$. D'autre part, les points de $d$ se situant très loin de $O$ doivent avoir pour image des points très proches de $O$. On dit souvent par abus de langage que "le point à l'infini est envoyé sur $O$" et réciproquement que "$O$ est envoyé sur le point à l'infini". Il est en fait possible de montrer rigoureusement que l'image de la droite $d$ est exactement le cercle $d'$ passant par $A'$, $B'$ et $O$.
Il découle de la définition d'inversion que si un point $P$ a pour image $P'$ (par une certaine inversion), alors le point $P'$ a pour image $P$. Sur l'exemple ci-dessus, l'image de $A'$ par l'inversion est donc $A$, l'image de $\mathcal{C'}$ est $\mathcal{C}$, l'image de $B'$ est $B$, et l'image du cercle $d'$ est la droite $d$.
Propriétés
Nous donnons à présent les propriétés essentielles des inversions. Nous avons déjà observé certaines de celles-ci sur notre exemple, et nous conseillons au lecteur de dessiner les nouvelles propriétés pour se familiariser avec elles.Propriétés (inversions)
Une inversion de centre $O$ et de rapport $k$ :
- envoie une droite passant par $O$ sur elle-même;
- envoie une droite ne passant pas par $O$ sur un cercle passant par $O$;
- envoie un cercle centré en $O$ sur un cercle centré en $O$ (en particulier, le cercle centré en $O$ et de rayon $\sqrt{|k|}$ est envoyé sur lui-même);
- envoie un cercle passant par $O$ sur une droite ne contenant pas $O$;
- envoie un cercle renfermant $O$ sur un cercle renfermant $O$;
- envoie un cercle ne renfermant pas $O$ sur un cercle ne renfermant pas $O$.
On a aussi la propriété suivante, dont la démonstration est une application directe de la définition d'inversion. La figure plus haut permet de mieux visualiser la propriété.
Propriété
Soient $O$, $A$ et $B$ trois points non-alignés du plan et $k$ un réel non-nul. Si $A'$ et $B'$ sont les images respectives de $A$ et $B$ par l'inversion de centre $O$ et de rapport $k$, alors les triangles $OA'B'$ et $OBA$ sont semblables.
Démonstration
On a par définition que $|OA| \cdot |OA'| = |OB| \cdot |OB'|$, donc $\dfrac{|OA|}{|OB|} = \dfrac{|OB'|}{|OA'|}$. Puisque de plus, $\widehat{AOB} = \widehat{A'OB'}$, les triangles $OA'B'$ et $OBA$ sont semblables.
2. Théorème de Ptolémée
Comme mentionné précédemment, une manière d'utiliser l'inversion dans la résolution d'un problème consiste à appliquer une inversion (bien choisie) à l'entièreté de la figure et à travailler sur la nouvelle figure obtenue plutôt que sur l'originale. L'idée d'appliquer une inversion de cette façon peut venir lorsque l'on est en présence d'une figure contenant beaucoup de cercles. En effet, une inversion pourrait alors transformer certains de ceux-ci en droites et faciliter les raisonnements.
Pour illustrer cette méthode, nous allons démontrer les deux sens du théorème de Ptolémée à l'aide d'une inversion. Rappelons son énoncé :
Nous avions donné la démonstration du sens $\Rightarrow$ dans le chapitre sur les quadrilatères cycliques, mais le sens $\Leftarrow$ n'avait pas été donné car il est difficile à démontrer sans faire usage d'une inversion. Ceci montre bien la puissance d'une telle méthode.
Nous démontrons les deux sens du théorème de Ptolémée d'un seul coup.
Pour illustrer cette méthode, nous allons démontrer les deux sens du théorème de Ptolémée à l'aide d'une inversion. Rappelons son énoncé :
Théorème de Ptolémée
Un quadrilatère (non croisé) $ABCD$ est cyclique si et seulement si
$$|AC|\cdot |BD| = |AB| \cdot |CD| + |BC| \cdot |AD|,$$ c'est-à-dire si le produit des longueurs de ses diagonales est égal à la somme des produits des longueurs des côtés opposés.
$$|AC|\cdot |BD| = |AB| \cdot |CD| + |BC| \cdot |AD|,$$ c'est-à-dire si le produit des longueurs de ses diagonales est égal à la somme des produits des longueurs des côtés opposés.
Nous avions donné la démonstration du sens $\Rightarrow$ dans le chapitre sur les quadrilatères cycliques, mais le sens $\Leftarrow$ n'avait pas été donné car il est difficile à démontrer sans faire usage d'une inversion. Ceci montre bien la puissance d'une telle méthode.
Nous démontrons les deux sens du théorème de Ptolémée d'un seul coup.
Démonstration
Considérons l'inversion de centre $A$ et de rapport $1$. Les images des points $B$, $C$ et $D$ sont notées $B'$, $C'$ et $D'$, comme sur la figure suivante.
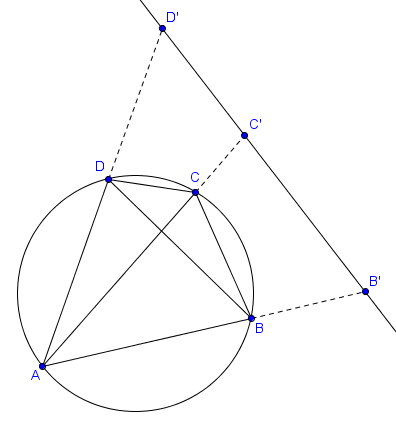
Les points $A, B, C, D$ sont cocycliques si et seulement si les points $B'$, $C'$ et $D'$ sont alignés. Cela vient en effet du fait que l'image d'un cercle passant par $A$ par une inversion de centre $A$ est une droite ne passant pas par $A$ (et vice versa). Or, le fait que $B'$, $C'$ et $D'$ sont alignés peut se traduire par l'égalité $|B'C'|+|C'D'|=|B'D'|$. Nous calculons alors les longueurs $|B'C'|$, $|C'D'|$ et $|B'D'|$ en fonctions des points $A, B, C, D$.
Les triangles $ABC$ et $AC'B'$ sont semblables, ce qui se traduit par
$$\frac{|B'C'|}{|BC|} = \frac{|AB'|}{|AC|}.$$ Comme $|AB'| \cdot |AB| = 1$ (car on considère l'inversion de centre $A$ et de rapport $1$), il s'ensuit que
$$|B'C'| = \frac{|BC|}{|AC| \cdot |AB|}.$$ De la même façon, les triangles $ACD$ et $AD'C'$ sont semblables ainsi que les triangles $ABD$ et $AD'B'$. On obtient donc similairement que
$$|C'D'| = \frac{|CD|}{|AC| \cdot |AD|} \quad \text{et}\quad |B'D'| = \frac{|BD|}{|AB| \cdot |AD|}.$$ L'égalité $|B'D'| = |B'C'|+|C'D'|$ est alors équivalente à
$$\frac{|BC|}{|AC| \cdot |AB|} + \frac{|CD|}{|AC| \cdot |AD|} = \frac{|BD|}{|AB| \cdot |AD|},$$ qui est elle-même équivalente (en la multipliant par $|AB| \cdot |AC| \cdot |AD|$) à
$$|BC| \cdot |AD| + |CD| \cdot |AB| = |BD| \cdot |AC|.$$

Les points $A, B, C, D$ sont cocycliques si et seulement si les points $B'$, $C'$ et $D'$ sont alignés. Cela vient en effet du fait que l'image d'un cercle passant par $A$ par une inversion de centre $A$ est une droite ne passant pas par $A$ (et vice versa). Or, le fait que $B'$, $C'$ et $D'$ sont alignés peut se traduire par l'égalité $|B'C'|+|C'D'|=|B'D'|$. Nous calculons alors les longueurs $|B'C'|$, $|C'D'|$ et $|B'D'|$ en fonctions des points $A, B, C, D$.
Les triangles $ABC$ et $AC'B'$ sont semblables, ce qui se traduit par
$$\frac{|B'C'|}{|BC|} = \frac{|AB'|}{|AC|}.$$ Comme $|AB'| \cdot |AB| = 1$ (car on considère l'inversion de centre $A$ et de rapport $1$), il s'ensuit que
$$|B'C'| = \frac{|BC|}{|AC| \cdot |AB|}.$$ De la même façon, les triangles $ACD$ et $AD'C'$ sont semblables ainsi que les triangles $ABD$ et $AD'B'$. On obtient donc similairement que
$$|C'D'| = \frac{|CD|}{|AC| \cdot |AD|} \quad \text{et}\quad |B'D'| = \frac{|BD|}{|AB| \cdot |AD|}.$$ L'égalité $|B'D'| = |B'C'|+|C'D'|$ est alors équivalente à
$$\frac{|BC|}{|AC| \cdot |AB|} + \frac{|CD|}{|AC| \cdot |AD|} = \frac{|BD|}{|AB| \cdot |AD|},$$ qui est elle-même équivalente (en la multipliant par $|AB| \cdot |AC| \cdot |AD|$) à
$$|BC| \cdot |AD| + |CD| \cdot |AB| = |BD| \cdot |AC|.$$
3. Polarisation
Étant donné un cercle de centre $O$ et de rayon $R$ dans le plan, on peut également considérer la polarisation par rapport à ce cercle. Ce qui distingue cette transformation de toutes celles qui ont déjà été étudiées sur ce site, c'est que l'image d'un point n'est plus un point mais une droite. Il ne s'agit donc pas réellement d'une transformation du plan qui peut être appliquée à toute une figure. On dira juste que certaines droites sont les polaires de certains points, et on essayera d'en déduire des informations utiles à partir des propriétés de la polarisation.
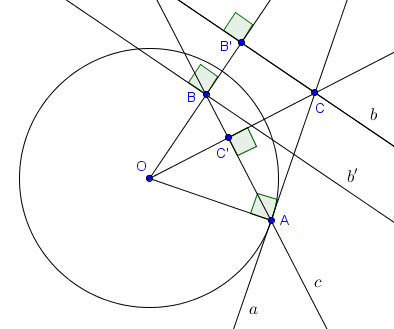
Sur la figure suivante, on considère la polarisation par rapport au cercle de centre $O$ passant par $A$. La polaire de $A$ est la droite $a$ tangente au cercle et passant par $A$. Les polaires respectives de $B$ et $B'$ sont les droites $b$ et $b'$ (car, sur cette figure, $B'$ est l'image de $B$ par l'inversion de centre $O$ et de rapport $|OA|^2$). Un fait important, qui fait appel aux propriétés des polarisations, est que la polaire du point $C$ (intersection de $a$ et $b$) est exactement la droite $c$ passant par $A$ et $B$.
Une autre propriété utile, mais moins évidente, est la suivante. Une façon de la prouver est d'utiliser le théorème de Pascal.
À noter que les points $A, B, C, D$ peuvent être dans un ordre quelconque sur le cercle. Cela signifie donc que la polaire de $Q$ est $PR$ et que la polaire de $R$ est $PQ$.
Avant cela, signalons le fait remarquable suivant : dans un triangle, la polaire du point de Lemoine par rapport au cercle circonscrit au triangle est exactement la droite de Lemoine du triangle. Les définitions du point et de la droite de Lemoine sont données dans les chapitres Triangles (suite) et Cercles d'Apollonius respectivement.
Définition
Fixons un cercle $\mathcal{C}$ de centre $O$ et de rayon $R$. Étant donné un point $P$ différent de $O$, on définit la polaire de $P$ par rapport à $\mathcal{C}$ comme suit. Soit $P'$ l'image de $P$ par l'inversion de centre $O$ et de rapport $R^2$, c'est-à-dire l'unique point de $[OP)$ tel que $|OP| \cdot |OP'| = R^2$. Alors la polaire de $P$ est définie comme étant la droite perpendiculaire à $OP$ et passant par $P'$. Si $d$ est la polaire de $P$ par rapport à $\mathcal{C}$, alors on dit aussi que $P$ est le pôle de $d$ (par rapport à $\mathcal{C}$).Sur la figure suivante, on considère la polarisation par rapport au cercle de centre $O$ passant par $A$. La polaire de $A$ est la droite $a$ tangente au cercle et passant par $A$. Les polaires respectives de $B$ et $B'$ sont les droites $b$ et $b'$ (car, sur cette figure, $B'$ est l'image de $B$ par l'inversion de centre $O$ et de rapport $|OA|^2$). Un fait important, qui fait appel aux propriétés des polarisations, est que la polaire du point $C$ (intersection de $a$ et $b$) est exactement la droite $c$ passant par $A$ et $B$.

Propriétés
Tout comme les inversions, les polarisations ont beaucoup de propriétés assez naturelles. Celles-ci ne sont pas compliquées à démontrer (et il peut être bon, comme exercice, d'essayer d'en donner une démonstration). Pour autant, elles n'en sont pas moins essentielles.Propriétés (polarisations)
Considérons une polarisation par rapport à un cercle $\mathcal{C}$ de centre $O$ et de rayon $R$.
- La polaire d'un point $P$ appartenant à $\mathcal{C}$ est la tangente à $\mathcal{C}$ en $P$.
- La polaire d'un point $P$ intérieur à $\mathcal{C}$ est une droite extérieure à $\mathcal{C}$.
- La polaire d'un point $P$ extérieur à $\mathcal{C}$ peut être construite comme suit : soient $S$ et $T$ les points de tangence des deux tangentes à $\mathcal{C}$ issues de $P$. Alors la polaire de $P$ est la droite $ST$.
- Si un point $P$ se trouve sur la polaire d'un point $Q$, alors $Q$ se situe sur la polaire de $P$.
- Si deux points $A$ et $B$ ont pour polaires deux droites s'intersectant en un point $C$, alors la polaire de $C$ est la droite $AB$.
- Les polaires de trois points alignés sont concourantes. (NB : si les trois points sont également alignés avec $O$, alors les droites sont concourantes "à l'infini", ce qui signifie qu'elles sont parallèles.)
Une autre propriété utile, mais moins évidente, est la suivante. Une façon de la prouver est d'utiliser le théorème de Pascal.
Propriété
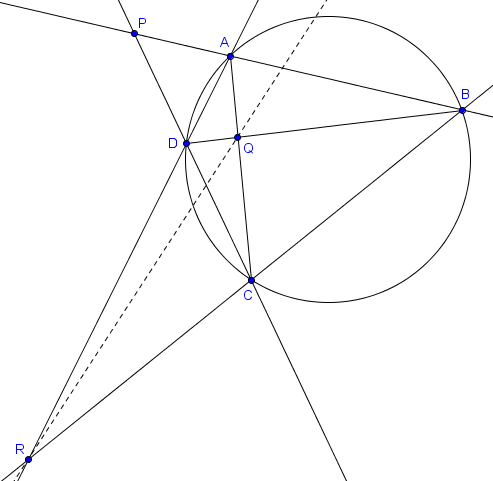
- Soient $A, B, C, D$ quatre points sur un cercle $\mathcal{C}$. On note $P$ l'intersection de $AB$ et $CD$, $Q$ l'intersection de $AC$ et $BD$, et $R$ l'intersection de $AD$ et $BC$ (en supposant qu'elles existent). Alors la polaire de $P$ par rapport à $\mathcal{C}$ est la droite $QR$.
À noter que les points $A, B, C, D$ peuvent être dans un ordre quelconque sur le cercle. Cela signifie donc que la polaire de $Q$ est $PR$ et que la polaire de $R$ est $PQ$.

Utilisation
Comme d'habitude, remarquer dans un problème qu'une certaine droite est la polaire d'un certain point (par rapport à un certain cercle) peut donner l'idée d'étudier cette polarisation plus en profondeur et de regarder quels sont les polaires des points de la figure. Dans le point théorique suivant, nous donnons deux exemples d'applications d'une polarisation qui permettent de résoudre un problème de géométrie.Avant cela, signalons le fait remarquable suivant : dans un triangle, la polaire du point de Lemoine par rapport au cercle circonscrit au triangle est exactement la droite de Lemoine du triangle. Les définitions du point et de la droite de Lemoine sont données dans les chapitres Triangles (suite) et Cercles d'Apollonius respectivement.
4. Exemples d'application
Considérons le problème suivant.
Voici un autre problème, un peu plus compliqué :
(Ces deux problèmes et leurs solutions proviennent de ce PDF. D'autres problèmes utilisant la polarisation s'y trouvent également et peuvent être consultés pour approfondir son entraînement.)
Problème
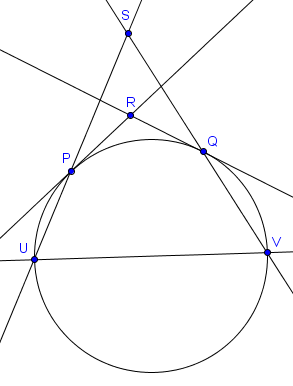
Soit $\mathcal{C}$ un cercle et $[UV]$ un de ses diamètres. On prend $P$ et $Q$ deux points sur $\mathcal{C}$, du même côté de $UV$ et avec $P$ plus proche de $U$ que $Q$. Les tangentes à $\mathcal{C}$ par $P$ et $Q$ s'intersectent en $R$. Si $S$ est le point d'intersection de $UP$ et $VQ$, alors montrer que $RS$ est perpendiculaire à $UV$.

Solution
Il s'agit typiquement du genre de problème où la polarisation pourrait être utile : il y a un cercle, des tangentes à ce cercle, et il faut démontrer qu'une droite ($RS$) est perpendiculaire à un certain diamètre ($UV$). En termes de polarisation, cette thèse signifie que $RS$ doit être la polaire par rapport à $\mathcal{C}$ d'un point appartenant à $UV$.
Il est donc naturel de considérer la polarisation par rapport à $\mathcal{C}$ et d'essayer de prouver que $RS$ est la polaire d'un point particulier de $UV$. Autrement dit, il suffit de prouver que le pôle de la droite $RS$ se situe sur $UV$. Nous savons déjà que la polaire de $R$ est exactement $PQ$ (voir point 3 dans les premières propriétés des polaires). Cela signifie que le pôle de $RS$ se situe sur $PQ$ (voir point 4). De plus, par le point 7, la polaire de $S$ est la droite $d$ passant par $PQ \cap UV$ et $PV \cap UQ$. À nouveau par le point 4 cela signifie que le pôle de $RS$ se situe sur cette droite $d$. De ces deux constatations, il découle que le pôle de $RS$ est le point d'intersection de $PQ$ et de $d$. Comme la droite $d$ passe par $PQ \cap UV$, l'intersection de ces deux droites est $PQ \cap UV$. On a donc bien démontré que le pôle de $RS$ se situe sur $UV$, ce qui implique que $RS$ est perpendiculaire à $UV$.
Notez que cet argument ne fonctionne pas quand $PQ$ est parallèle à $UV$ (car on ne peut alors pas appliquer le point 7). Cependant, si $PQ$ est parallèle à $UV$ alors la figure est complètement symétrique et il est évident que $RS$ est la médiatrice de $[UV]$.
Il est donc naturel de considérer la polarisation par rapport à $\mathcal{C}$ et d'essayer de prouver que $RS$ est la polaire d'un point particulier de $UV$. Autrement dit, il suffit de prouver que le pôle de la droite $RS$ se situe sur $UV$. Nous savons déjà que la polaire de $R$ est exactement $PQ$ (voir point 3 dans les premières propriétés des polaires). Cela signifie que le pôle de $RS$ se situe sur $PQ$ (voir point 4). De plus, par le point 7, la polaire de $S$ est la droite $d$ passant par $PQ \cap UV$ et $PV \cap UQ$. À nouveau par le point 4 cela signifie que le pôle de $RS$ se situe sur cette droite $d$. De ces deux constatations, il découle que le pôle de $RS$ est le point d'intersection de $PQ$ et de $d$. Comme la droite $d$ passe par $PQ \cap UV$, l'intersection de ces deux droites est $PQ \cap UV$. On a donc bien démontré que le pôle de $RS$ se situe sur $UV$, ce qui implique que $RS$ est perpendiculaire à $UV$.
Notez que cet argument ne fonctionne pas quand $PQ$ est parallèle à $UV$ (car on ne peut alors pas appliquer le point 7). Cependant, si $PQ$ est parallèle à $UV$ alors la figure est complètement symétrique et il est évident que $RS$ est la médiatrice de $[UV]$.
Voici un autre problème, un peu plus compliqué :
Problème (China Western Math Olympiad 2006)
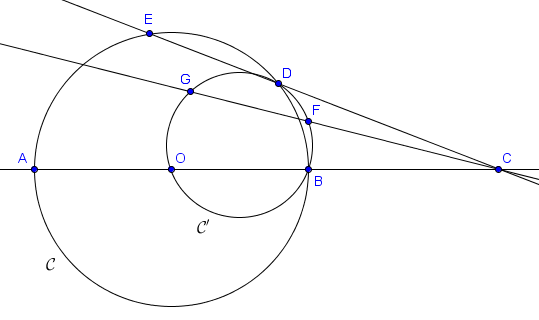
Soit $\mathcal{C}$ un cercle de centre $O$, et $[AB]$ un diamètre de $\mathcal{C}$. Soit $C$ un point de $AB$ en dehors de $[AB]$, plus proche de $B$ que de $A$. Une droite passant par $C$ coupe $\mathcal{C}$ en $D$ et $E$. Le point $F$ est défini de sorte que $[OF]$ soit un diamètre du cercle circonscrit $\mathcal{C}'$ au triangle $BOD$. Enfin, la droite $CF$ intersecte $\mathcal{C}'$ à nouveau en $G$. Montrer que les points $O, A, E, G$ sont cocyliques.

Démonstration
La situation du point $C$ peut donner envie de s'intéresser à sa polaire par rapport à $\mathcal{C}$. Par le point 7, on sait que cette polaire est la droite passant par $P = AE \cap DB$ et $Q = EB \cap DA$. De la même manière, la polaire de $P$ est $CQ$. En particulier, $CQ$ est perpendiculaire à $OP$.
Notons $R$ l'intersection de ces deux droites perpendiculaires $CQ$ et $OP$. Sur le dessin ci-dessous, il semble que $R$ coïncide avec $G$ ! Si $R$ est effectivement égal à $G$, alors en particulier $G$ se situe sur $OP$ et on a successivement $|PE| \cdot |PA| = |PD| \cdot |PB| = |PG| \cdot |PO|$, ce qui implique que $AEGO$ est cyclique et termine le problème (on a ici utilisé les puissances de $P$ par rapport aux différents cercles). Il suffit donc pour conclure de prouver que $R = G$.
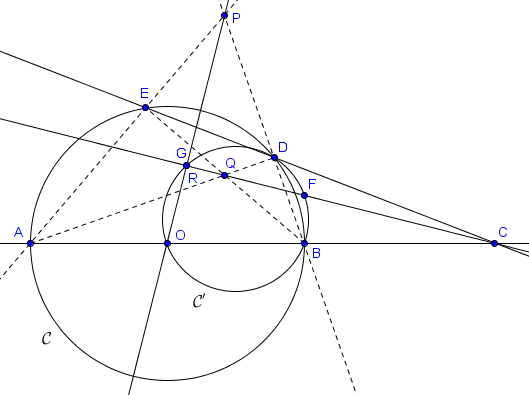
On a $\widehat{QRP} = 90^\circ = \widehat{QEP} = \widehat{QDP}$ (notez que $Q$ est l'orthocentre de $ABP$), donc les points $P, D, Q, R, E$ sont cocycliques. Donc $\widehat{DRP} = \widehat{DEP} = \widehat{ABP} = \widehat{OBD}$. Ainsi, le point $R$ se situe sur $\mathcal{C}'$. Mais on a aussi $\widehat{CRO} = 90^\circ$, donc $R$ se situe sur le cercle de diamètre $[CO]$. C'est aussi le cas de $G$ : il appartient à $\mathcal{C}'$ par définition et on a $\widehat{CGO} = \widehat{FGO} = 90^\circ$. Puisque le cercle de diamètre $[CO]$ n'intersecte $\mathcal{C'}$ qu'en un seul point différent de $O$, on en conclut que $R = G$.
Notons $R$ l'intersection de ces deux droites perpendiculaires $CQ$ et $OP$. Sur le dessin ci-dessous, il semble que $R$ coïncide avec $G$ ! Si $R$ est effectivement égal à $G$, alors en particulier $G$ se situe sur $OP$ et on a successivement $|PE| \cdot |PA| = |PD| \cdot |PB| = |PG| \cdot |PO|$, ce qui implique que $AEGO$ est cyclique et termine le problème (on a ici utilisé les puissances de $P$ par rapport aux différents cercles). Il suffit donc pour conclure de prouver que $R = G$.

On a $\widehat{QRP} = 90^\circ = \widehat{QEP} = \widehat{QDP}$ (notez que $Q$ est l'orthocentre de $ABP$), donc les points $P, D, Q, R, E$ sont cocycliques. Donc $\widehat{DRP} = \widehat{DEP} = \widehat{ABP} = \widehat{OBD}$. Ainsi, le point $R$ se situe sur $\mathcal{C}'$. Mais on a aussi $\widehat{CRO} = 90^\circ$, donc $R$ se situe sur le cercle de diamètre $[CO]$. C'est aussi le cas de $G$ : il appartient à $\mathcal{C}'$ par définition et on a $\widehat{CGO} = \widehat{FGO} = 90^\circ$. Puisque le cercle de diamètre $[CO]$ n'intersecte $\mathcal{C'}$ qu'en un seul point différent de $O$, on en conclut que $R = G$.
(Ces deux problèmes et leurs solutions proviennent de ce PDF. D'autres problèmes utilisant la polarisation s'y trouvent également et peuvent être consultés pour approfondir son entraînement.)