Théorie > Théorie des nombres > Théorème d'Euler-Fermat
Prérequis
Résumé
On est très vite amené, en théorie des nombres, à observer des puissances modulo un certain nombre. On peut par exemple se demander quel est le dernier chiffre du nombre $2013^{2013}$, ce qui revient à vouloir déterminer sa valeur modulo $10$. Le théorème d'Euler, dont un cas particulier est celui de Fermat, permet de répondre très facilement à cette question. Il s'agit d'un théorème fondamental : s'il ne fallait en retenir qu'un en théorie des nombres, ce serait certainement celui-là.
Ce chapitre a été écrit par N. Radu et mis en ligne le 8 décembre 2014.
1. Puissances
Observons le comportement des puissances successives de $2$ modulo différents nombres.
On a par exemple, modulo $7$ :
$$\begin{array}{c|cccccccc}
m & 0 & 1 & 2 & 3 & 4 & 5 & 6 & \ldots \\[2ex]
\hline
2^m \pmod 7 & 1 & 2& 4 & 1 & 2 & 4 &1 & \ldots
\end{array}$$ Ou modulo $5$ :
$$\begin{array}{c|cccccccc}
m & 0 & 1 & 2 & 3 & 4 & 5 & 6 & \ldots \\[2ex]
\hline
2^m \pmod 5 & 1 & 2& 4 & 3 & 1 & 2 & 4 &\ldots
\end{array}$$ Ou encore, modulo $6$ :
$$\begin{array}{c|cccccccc}
m & 0 & 1 & 2 & 3 & 4 & 5 & 6 & \ldots \\[2ex]
\hline
2^m \pmod 6 & 1 & 2& 4 & 2 & 4 & 2 & 4 &\ldots
\end{array}$$ Puisque pour passer d'une colonne à la suivante, on ne fait que multiplier par $2$, on peut toujours calculer une valeur à partir de la précédente. Cela signifie en particulier que les valeurs observées formeront toujours une suite périodique ! Dès que l'on retombe sur un élément que l'on a déjà rencontré, la suite devient périodique. Sur les deux premiers exemples, nous sommes retombés sur $1$ alors que sur le troisième, nous avons rencontré $2$ une seconde fois.
Nous aimerions comprendre ces suites en toute généralité, c'est-à-dire celles données par les valeurs modulo $n$ des puissances successives d'un nombre $a$. Sous quelle(s) condition(s) allons-nous retomber sur le nombre $1$ ? Et dans ce cas, après combien de temps ? Avant de pouvoir répondre à ces questions, il nous faut définir la fonction indicatrice d'Euler.
On a par exemple, modulo $7$ :
$$\begin{array}{c|cccccccc}
m & 0 & 1 & 2 & 3 & 4 & 5 & 6 & \ldots \\[2ex]
\hline
2^m \pmod 7 & 1 & 2& 4 & 1 & 2 & 4 &1 & \ldots
\end{array}$$ Ou modulo $5$ :
$$\begin{array}{c|cccccccc}
m & 0 & 1 & 2 & 3 & 4 & 5 & 6 & \ldots \\[2ex]
\hline
2^m \pmod 5 & 1 & 2& 4 & 3 & 1 & 2 & 4 &\ldots
\end{array}$$ Ou encore, modulo $6$ :
$$\begin{array}{c|cccccccc}
m & 0 & 1 & 2 & 3 & 4 & 5 & 6 & \ldots \\[2ex]
\hline
2^m \pmod 6 & 1 & 2& 4 & 2 & 4 & 2 & 4 &\ldots
\end{array}$$ Puisque pour passer d'une colonne à la suivante, on ne fait que multiplier par $2$, on peut toujours calculer une valeur à partir de la précédente. Cela signifie en particulier que les valeurs observées formeront toujours une suite périodique ! Dès que l'on retombe sur un élément que l'on a déjà rencontré, la suite devient périodique. Sur les deux premiers exemples, nous sommes retombés sur $1$ alors que sur le troisième, nous avons rencontré $2$ une seconde fois.
Nous aimerions comprendre ces suites en toute généralité, c'est-à-dire celles données par les valeurs modulo $n$ des puissances successives d'un nombre $a$. Sous quelle(s) condition(s) allons-nous retomber sur le nombre $1$ ? Et dans ce cas, après combien de temps ? Avant de pouvoir répondre à ces questions, il nous faut définir la fonction indicatrice d'Euler.
2. Indicatrice d'Euler
Définition
La fonction indicatrice d'Euler est définie pour $n \in \mathbb{N}_0$ par
$$\varphi(n) = \#\left\{ k \in \left\{1, 2, \ldots, n \right\} : (k, n) = 1\right\}$$ ou, autrement dit, $\varphi(n)$ est égal au nombre d'entiers entre $1$ et $n$ qui sont premiers avec $n$.
$$\varphi(n) = \#\left\{ k \in \left\{1, 2, \ldots, n \right\} : (k, n) = 1\right\}$$ ou, autrement dit, $\varphi(n)$ est égal au nombre d'entiers entre $1$ et $n$ qui sont premiers avec $n$.
Les premières valeurs de cette fonction sont données par le tableau suivant.
$$\begin{array}{c|c}
n & \varphi(n) \\[0.3em]
\hline
1 & 1 \\[0.3em]
2 & 1 \\[0.3em]
3 & 2\\[0.3em]
4 & 2\\[0.3em]
5 & 4\\[0.3em]
6 & 2\\[0.3em]
7 & 6
\end{array}$$ Par exemple, $\varphi(6) = 2$ car les seuls entiers entre $1$ et $6$ qui sont premiers avec $6$ sont $1$ et $5$.
Il ne semble a priori pas évident de calculer $\varphi(n)$ pour un $n$ quelconque, à part en regardant un par un les nombres entre $1$ et $n$. Il existe cependant une formule bien pratique permettant de calculer $\varphi(n)$ dès que l'on connait sa décomposition en facteurs premiers. Celle-ci se trouve en plusieurs étapes :
- Si $p$ est un nombre premier, alors $\varphi(p) = p-1$.
En effet, vu que $p$ est premier, tous les nombres entre $1$ et $p-1$ inclus sont premiers avec $p$. - Si $p$ est un nombre premier, alors $\varphi(p^m) = p^{m-1}(p-1)$.
Pour le comprendre, il suffit de se demander quels nombres entre $1$ et $p^m$ ne sont pas premiers avec $p^m$. Il s'agit des nombres ayant un facteur $p$, c'est-à-dire ceux qui sont divisibles par $p$. Ce sont donc simplement les entiers $p, 2p, 3p, \ldots, p^m$, qui sont au nombre de $p^{m-1}$. Le nombre d'entiers entre $1$ et $p^m$ qui sont premiers avec $p^m$ est dès lors égal à $p^m - p^{m-1} = p^{m-1}(p-1)$. - Si $a$ et $b$ sont premiers entre eux, alors $\varphi(ab) = \varphi(a)\cdot\varphi(b)$.
C'est le point le plus délicat à démontrer, et sa démonstration est donnée à titre informatif.
Il s'agit en fait d'une conséquence de théorème des restes chinois. Celui-ci nous dit en effet qu'il y a une correspondance entre les entiers de $\left\{1, 2, \ldots, ab\right\}$ et le produit cartésien $\left\{1, 2, \ldots, a\right\} \times \left\{1, 2, \ldots, b\right\}$. Elle consiste à associer au nombre $x$ le reste de sa division par $a$ et le reste de sa division par $b$ (en remplacant $0$ par $a$ ou $b$ mais cela a peu d'importance). Le théorème des restes chinois nous dit en fait qu'étant donnés les deux restes, il existe un unique $x$ duquel ils peuvent provenir. Or, on remarque que les nombres premiers avec $ab$ sont envoyés, par cette correspondance, exactement sur les couples $(y,z)$ où $y$ est premier avec $a$ et $z$ premier avec $b$. De là, il suit que $\varphi(ab) = \varphi(a)\cdot\varphi(b)$. - Si $n = p_1^{e_1} \cdot p_2^{e_2} \cdot \ldots \cdot p_k^{e_k}$, alors $\varphi(n) = p_1^{e_1 - 1}(p_1 - 1) \cdot \ldots \cdot p_k^{e_k - 1}(p_k - 1)$.
Cela découle directement des deux points précédents, vu que chaque $p_i^{e_i}$ est premier avec les autres $p_j^{e_j}$.
Cette formule peut également se réécrire d'une forme parfois plus utile :
Formule (fonction indicatrice d'Euler)
$$\begin{align}
\varphi(n) &= p_1^{e_1 - 1}(p_1 - 1) \cdot \ldots \cdot p_k^{e_k - 1}(p_k - 1)\\[0.5em]
&=n \cdot\left(1 - \frac{1}{p_1}\right)\cdot \ldots \cdot \left(1 - \frac{1}{p_k}\right)
\end{align}$$
\varphi(n) &= p_1^{e_1 - 1}(p_1 - 1) \cdot \ldots \cdot p_k^{e_k - 1}(p_k - 1)\\[0.5em]
&=n \cdot\left(1 - \frac{1}{p_1}\right)\cdot \ldots \cdot \left(1 - \frac{1}{p_k}\right)
\end{align}$$
D'un point de vue pratique, la première expression de cette formule nous indique que pour trouver $\varphi(n)$, il suffit de regarder la décomposition en facteurs premiers de $n$, et pour chaque facteur premier $p_i^{e_i}$ de remplacer un seul des $p_i$ par $p_i-1$.
Par exemple, pour $n = 3^3 \cdot 5^2$, on a $\varphi(n) = 3^2 \cdot 2 \cdot 5 \cdot 4$.
Les $100$ premières valeurs de $\varphi$ sont représentées sur le graphe suivant. Tous les points situés sur la diagonale correspondent aux nombres $n$ premiers, puisque ceux-ci donnent chacun $\varphi(n) = n-1$.
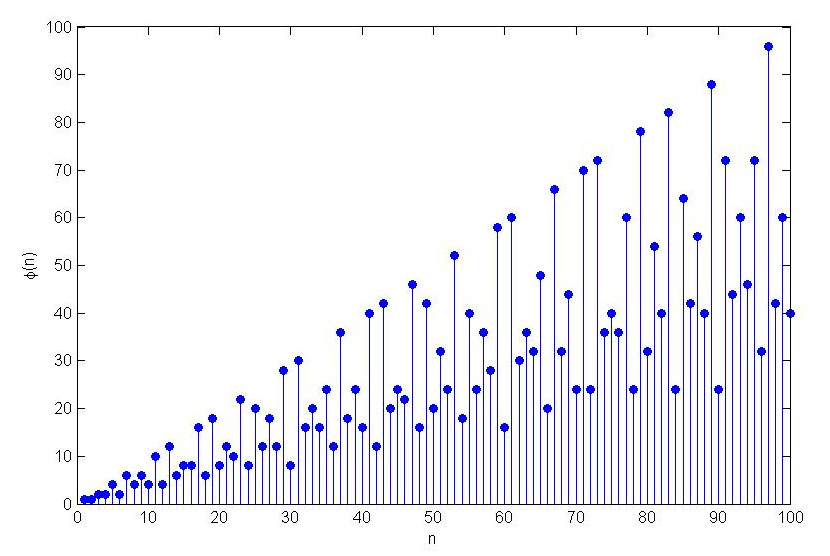
Premières valeurs de $\varphi$.
3. Théorème d'Euler-Fermat
Théorème d'Euler
Nous pouvons à présent énoncer et même démontrer le théorème d'Euler.Théorème d'Euler
Si $(a,n) = 1$, alors $$a^{\varphi(n)} \equiv 1 \pmod n$$ où $\varphi$ désigne la fonction indicatrice d'Euler.
Ce théorème nous indique donc que, dans la suite des puissances successives de $a$, nous retomberons toujours sur $1$ à la puissance $\varphi(n)$-ème. À noter cependant qu'il ne s'agit pas spécialement de la première fois où un $1$ apparaît à nouveau. Nous discuterons de cela dans le prochain point théorique.
Démonstration
NB : Nous travaillons modulo $n$ dans cette preuve et ne différencions donc pas deux nombres qui sont égaux modulo $n$.
Notons $A = \left\{a_1, a_2, \ldots, a_k\right\}$ l'ensemble des entiers de $\left\{0, 1, \ldots, n-1\right\}$ qui sont premiers avec $n$. On a donc $\#A = \varphi(n)$ par définition de la fonction indicatrice d'Euler (d'où $k = \varphi(n)$).
Remarquons à présent que si nous multiplions tous les éléments de $A$ par $a$ (celui de l'énoncé), alors les éléments de $A$ sont simplement permutés, c'est-à-dire
$$A = \left\{aa_1,aa_2, \ldots, aa_k\right\}.$$ Cela vient du fait que si $(a_j, n) = 1$, alors $(aa_j, n) = 1$ également puisque $a$ est premier avec $n$ (donc $a_j \in A \Rightarrow aa_j \in A$). De plus, deux éléments $a_i$ et $a_j$ distincts, lorsqu'ils sont multipliés par $a$, restent distincts (modulo $n$). En effet, si tel n'était pas le cas, on aurait $aa_i \equiv aa_j$ mais une simple multiplication par $a^{-1}$ rendrait $a_i \equiv a_j$ qui est impossible vu que $a_i$ et $a_j$ étaient supposés différents.
Pour mieux comprendre ce phénomène, regardons ce que cela signifie pour $n = 8$ et $a = 5$. Dans ce cas, on a $A = \left\{1, 3, 5, 7\right\}$ et, en multipliant chaque élément par $5$, on obtient $\left\{5, 15, 25, 35\right\} = \left\{5, 7, 1, 3\right\}$ (comme nous travaillons modulo $8$). Nous sommes donc bien retombés sur les éléments de $A$.
Reprenons la preuve en général. Les éléments de $A$ étant exactement les mêmes que ceux de $\left\{aa_1,aa_2, \ldots, aa_k\right\}$; multiplier entre eux tous les éléments de $A$ revient exactement à multiplier ceux de $\left\{aa_1,aa_2, \ldots, aa_k\right\}$. On a donc
$$\begin{align}
a_1 \cdot a_2 \cdot \ldots \cdot a_k & \equiv aa_1 \cdot aa_2 \cdot \ldots \cdot aa_k \pmod n\\
& \equiv a^k \cdot a_1 \cdot \ldots \cdot a_k \pmod n.
\end{align}$$ Les éléments $a_1, \ldots, a_k$ étant tous inversibles, nous pouvons multiplier les deux membres de cette dernière égalité par $a_1^{-1} \cdot \ldots \cdot a_k^{-1}$ pour obtenir
$$1 \equiv a^k \pmod n$$ qui est exactement l'énoncé du théorème d'Euler puisque $k = \varphi(n)$.
Notons $A = \left\{a_1, a_2, \ldots, a_k\right\}$ l'ensemble des entiers de $\left\{0, 1, \ldots, n-1\right\}$ qui sont premiers avec $n$. On a donc $\#A = \varphi(n)$ par définition de la fonction indicatrice d'Euler (d'où $k = \varphi(n)$).
Remarquons à présent que si nous multiplions tous les éléments de $A$ par $a$ (celui de l'énoncé), alors les éléments de $A$ sont simplement permutés, c'est-à-dire
$$A = \left\{aa_1,aa_2, \ldots, aa_k\right\}.$$ Cela vient du fait que si $(a_j, n) = 1$, alors $(aa_j, n) = 1$ également puisque $a$ est premier avec $n$ (donc $a_j \in A \Rightarrow aa_j \in A$). De plus, deux éléments $a_i$ et $a_j$ distincts, lorsqu'ils sont multipliés par $a$, restent distincts (modulo $n$). En effet, si tel n'était pas le cas, on aurait $aa_i \equiv aa_j$ mais une simple multiplication par $a^{-1}$ rendrait $a_i \equiv a_j$ qui est impossible vu que $a_i$ et $a_j$ étaient supposés différents.
Pour mieux comprendre ce phénomène, regardons ce que cela signifie pour $n = 8$ et $a = 5$. Dans ce cas, on a $A = \left\{1, 3, 5, 7\right\}$ et, en multipliant chaque élément par $5$, on obtient $\left\{5, 15, 25, 35\right\} = \left\{5, 7, 1, 3\right\}$ (comme nous travaillons modulo $8$). Nous sommes donc bien retombés sur les éléments de $A$.
Reprenons la preuve en général. Les éléments de $A$ étant exactement les mêmes que ceux de $\left\{aa_1,aa_2, \ldots, aa_k\right\}$; multiplier entre eux tous les éléments de $A$ revient exactement à multiplier ceux de $\left\{aa_1,aa_2, \ldots, aa_k\right\}$. On a donc
$$\begin{align}
a_1 \cdot a_2 \cdot \ldots \cdot a_k & \equiv aa_1 \cdot aa_2 \cdot \ldots \cdot aa_k \pmod n\\
& \equiv a^k \cdot a_1 \cdot \ldots \cdot a_k \pmod n.
\end{align}$$ Les éléments $a_1, \ldots, a_k$ étant tous inversibles, nous pouvons multiplier les deux membres de cette dernière égalité par $a_1^{-1} \cdot \ldots \cdot a_k^{-1}$ pour obtenir
$$1 \equiv a^k \pmod n$$ qui est exactement l'énoncé du théorème d'Euler puisque $k = \varphi(n)$.
Remarque : Si $(a,n) \neq 1$, alors il est aisé de comprendre que la seule puissance de $a$ donnant $1$ modulo $n$ est $a^0 = 1$. En effet, pour $m > 0$, $a^m$ partage un facteur avec $n$ et $a^m - 1$ ne peut dès lors pas être divisible par $n$. Dans un tel cas, il convient alors de séparer $n$ en sa partie possédant des facteurs communs avec $a$ et celle première avec $a$ pour analyser les puissances de $a$ à l'aide du théorème d'Euler.
Théorème de Fermat
Le théorème de Fermat (nous parlons ici du petit théorème de Fermat, le grand étant bien différent) est un corollaire immédiat du théorème d'Euler. Il s'agit du cas particulier où $n$ est un nombre premier.Théorème de Fermat
Si $a$ n'est pas divisible par $p$ premier, alors
$$a^{p-1} \equiv 1 \pmod p.$$
$$a^{p-1} \equiv 1 \pmod p.$$
4. Ordre multiplicatif
Reprenons nos exemples initiaux et observons ce que le théorème d'Euler nous a apporté. Il ne nous a évidemment rien appris de plus que ce que l'on connaissait déjà vu que nos exemples étaient très petits, mais nous pouvons observer sur ceux-ci la puissance du théorème.
Pour $n = 5$ et $a = 2$, nous avions
$$\begin{array}{c|cccccccc}
m & 0 & 1 & 2 & 3 & 4 & 5 & 6 & \ldots \\[2ex]
\hline
2^m \pmod 5 & 1 & 2& 4 & 3 & \boxed{1} & 2 & 4 &\ldots
\end{array}$$ Le théorème d'Euler (en fait, le théorème de Fermat vu que $5$ est premier), nous indique dans ce cas que
$$2^4 \equiv 1 \pmod 5.$$ Il s'agit du $1$ encadré dans notre tableau, et on remarque qu'il s'agit en fait de la première fois où $1$ réapparaît.
Pour $n = 7$ et $a = 2$, nous avions par contre
$$\begin{array}{c|cccccccc}
m & 0 & 1 & 2 & 3 & 4 & 5 & 6 & \ldots \\[2ex]
\hline
2^m \pmod 7 & 1 & 2& 4 & 1 & 2 & 4 &\boxed{1} & \ldots
\end{array}$$ et le théorème de Fermat nous apporte ici
$$2^6 \equiv 1 \pmod 7.$$ Il ne s'agit cette fois-ci pas de la première fois que le nombre $1$ réapparaît.
Pour $n = 5$ et $a = 2$, nous avions
$$\begin{array}{c|cccccccc}
m & 0 & 1 & 2 & 3 & 4 & 5 & 6 & \ldots \\[2ex]
\hline
2^m \pmod 5 & 1 & 2& 4 & 3 & \boxed{1} & 2 & 4 &\ldots
\end{array}$$ Le théorème d'Euler (en fait, le théorème de Fermat vu que $5$ est premier), nous indique dans ce cas que
$$2^4 \equiv 1 \pmod 5.$$ Il s'agit du $1$ encadré dans notre tableau, et on remarque qu'il s'agit en fait de la première fois où $1$ réapparaît.
Pour $n = 7$ et $a = 2$, nous avions par contre
$$\begin{array}{c|cccccccc}
m & 0 & 1 & 2 & 3 & 4 & 5 & 6 & \ldots \\[2ex]
\hline
2^m \pmod 7 & 1 & 2& 4 & 1 & 2 & 4 &\boxed{1} & \ldots
\end{array}$$ et le théorème de Fermat nous apporte ici
$$2^6 \equiv 1 \pmod 7.$$ Il ne s'agit cette fois-ci pas de la première fois que le nombre $1$ réapparaît.
Ordre multiplicatif d'un nombre modulo $n$
Vu que $\varphi(n)$ n'est visiblement pas toujours la plus petite puissance strictement positive qu'il faut mettre à l'entier $a$ pour obtenir $1$ modulo $n$, il est naturel de donner un nom et une notation à cette plus petite puissance.Définition
Si $(a,n) = 1$, l'ordre multiplicatif de $a$ modulo $n$ est le plus petit entier strictement positif $m$ tel que $a^m \equiv 1 \pmod n$. On note ce nombre $o_n(a)$ (on omet parfois l'indice $n$ lorsqu'il est fixé par le contexte).
Petites propriétés
Les propriétés suivantes ne sont pas difficiles mais sont souvent bien utiles.Propriété 1
Si $(a,n)=1$, alors $a^m \equiv 1 \pmod n$ avec $m \in \mathbb{N}$ si et seulement si $o_n(a)$ divise $m$.
Démonstration
Le sens $\Leftarrow$ est le plus facile. Si $o_n(a)$ divise $m$, cela signifie que $m = o_n(a)\cdot k$ pour un entier $k$. Dès lors, vu que $a^{o_n(a)} \equiv 1 \pmod n$ par définition de l'ordre multiplicatif, on a
$$a^m \equiv a^{o_n(a)\cdot k} \equiv \left(a^{o_n(a)}\right)^k \equiv 1^k \equiv 1 \pmod n.$$ Pour le sens $\Rightarrow$, on considère la division euclidienne de $m$ par $o_n(a)$ :
$$m = q\cdot o_n(a) + r \quad \text{où} \quad r \in \left\{0, \ldots, o_n(a)-1\right\}.$$ On a alors
$$1 \equiv a^m \equiv a^{q\cdot o_n(a) + r}\equiv \left(a^{o_n(a)}\right)^q \cdot a^r \equiv a^r \pmod n.$$ Vu que $r$ est un naturel inférieur à $o_n(a)$, on doit forcément avoir $r = 0$. En effet, sinon on aurait trouvé un exposant non nul inférieur à $o_n(a)$ tel que $a^r$ rend $1$ modulo $n$, ce qui est impossible vu que $o_n(a)$ est le plus petit nombre vérifiant cette propriété.
$$a^m \equiv a^{o_n(a)\cdot k} \equiv \left(a^{o_n(a)}\right)^k \equiv 1^k \equiv 1 \pmod n.$$ Pour le sens $\Rightarrow$, on considère la division euclidienne de $m$ par $o_n(a)$ :
$$m = q\cdot o_n(a) + r \quad \text{où} \quad r \in \left\{0, \ldots, o_n(a)-1\right\}.$$ On a alors
$$1 \equiv a^m \equiv a^{q\cdot o_n(a) + r}\equiv \left(a^{o_n(a)}\right)^q \cdot a^r \equiv a^r \pmod n.$$ Vu que $r$ est un naturel inférieur à $o_n(a)$, on doit forcément avoir $r = 0$. En effet, sinon on aurait trouvé un exposant non nul inférieur à $o_n(a)$ tel que $a^r$ rend $1$ modulo $n$, ce qui est impossible vu que $o_n(a)$ est le plus petit nombre vérifiant cette propriété.
Proposition 2
Si $(a,n) = 1$, $o_n(a)$ divise $\varphi(n)$.
Démonstration
Il s'agit là d'une réécriture du théorème d'Euler à l'aide de $o_n(a)$. En effet, la propriété précédente nous montre que le théorème $a^{\varphi(n)} \equiv 1 \pmod n$ est équivalent à dire que $o_n(a)$ divise $\varphi(n)$.
Proposition 3
Si $(a,n) = 1$, les nombres $a^0, a^1, a^2, \ldots, a^{o_n(a)-1}$ sont distincts deux à deux modulo $n$.
Démonstration
On procède par l'absurde. Supposons avoir $i, j \in \left\{0, 1, \ldots, o_n(a)-1\right\}$ distincts tels que $a^i \equiv a^j \pmod n$. On peut sans perte de généralité supposer que $i > j$. Vu que $a$ est inversible modulo $n$, on peut multiplier les deux membres par $a^{-j}$ pour obtenir
$$a^{i-j} \equiv 1 \pmod n.$$ Il s'agit là d'une contradiction, car nous avons trouvé un exposant ($i-j$) non nul et inférieur à $o_n(a)$ qui donne $1$ modulo $n$.
$$a^{i-j} \equiv 1 \pmod n.$$ Il s'agit là d'une contradiction, car nous avons trouvé un exposant ($i-j$) non nul et inférieur à $o_n(a)$ qui donne $1$ modulo $n$.
Retour sur notre exemple
Pour $n = 7$ et $a = 2$, nous avons vu plus haut que $o_n(a) = 3$. On peut vérifier que les trois propriétés ci-dessus sont bien correctes :- On voit bien sur notre tableau que $2^m \equiv 1 \pmod 7$ si et seulement si $m$ est un multiple de $3$.
- $\varphi(7) = 6$ est bien divisible par $3$.
- Les nombres $2^0$, $2^1$ et $2^2$ sont égaux à $1$, $2$ et $4$ respectivement qui sont bien différents modulo $7$. Il s'agit en fait de la suite de nombres qui apparaît périodiquement.