Théorie > Algèbre > Polynômes (suite)
Prérequis
Résumé
Il existe un grand nombre de résultats faisant intervenir des polynômes. Nous expliquons ici les formules de Viète, la formule d'interpolation de Lagrange et la formule de Taylor. Nous nous intéressons ensuite à l'irréductibilité des polynômes à coefficients rationnels ou entiers.
Ce chapitre a été écrit par N. Radu et mis en ligne le 8 décembre 2014.
1. Formules de Viète
Nous avons vu que tout polynôme $P$ à coefficients complexes pouvait s'écrire de deux manières bien distinctes. La première est simplement l'écriture habituelle des polynômes avec leurs coefficients :
$$P(x) = c_n x^n + c_{n-1}x^{n-1} + \ldots + c_1 x + c_0$$ La deuxième fait intervenir les $n$ racines (comptées avec leur multiplicité) $r_1, r_2, \ldots, r_n$ de $P$ :
$$P(x) = c_n (x-r_1)(x-r_2)\ldots(x-r_n)$$ Puisqu'il s'agit de deux façons d'écrire un seul et même polynôme, on peut directement trouver des formules reliant les coefficients $c_i$ aux racines $r_i$. En effet, pour chaque $i \in \{0, 1, \ldots, n\}$, on peut calculer le coefficient de $x^i$ à partir de la deuxième forme et on sait qu'il doit être égal à $c_i$. Par exemple, pour $n = 3$, on peut développer la deuxième forme et obtenir
$$\begin{align}
P(x) &= c_3(x-r_1)(x-r_2)(x-r_3) \\
&= c_3(x^3 - (r_1+r_2+r_3)x^2 + (r_1r_2 + r_2r_3 + r_3r_1) x - r_1r_2r_3)
\end{align}$$ On en déduit que l'on a les formules (pour $n = 3$) :
$$\left\{ \begin{array}{l}
c_2 = -c_3 (r_1+r_2+r_3) \\[1mm]
c_1 = c_3 (r_1r_2 + r_2 r_3 + r_3r_1) \\[1mm]
c_0 = -c_3 (r_1r_2r_3)
\end{array}\right.
\quad \Leftrightarrow \quad
\left\{ \begin{array}{l}
r_1+r_2+r_3 = -\frac{c_2}{c_3}\\
r_1r_2 + r_2 r_3 + r_3r_1 = \frac{c_1}{c_3} \\
r_1r_2r_3 = -\frac{c_0}{c_3}
\end{array}\right.
$$ On peut effectuer le même raisonnement pour un polynôme de degré $n$, et on trouve les formules suivantes.
Lorsqu'on est en présence d'un polynôme sous sa forme habituelle, on peut donc directement connaître la somme et le produit de ses racines en calculant $\displaystyle -\frac{c_{n-1}}{c_n}$ et $\displaystyle (-1)^n \cdot \frac{c_0}{c_n}$. On peut également connaître la somme de tous les produits de $k$ racines, ces formules étant plus rarement utilisées (mais il ne faut pas pour autant les oublier). En particulier, si le polynôme est unitaire, c'est-à-dire si $c_n = 1$, alors les coefficients donnent directement ces valeurs (au signe près).
Exemple : Soit $P(x) = 4x^5 - 3 x^4 + 2x^2 + 1$. La somme des $5$ racines de $P$ est égale à $\frac{3}{4}$ et le produit de celles-ci est égal à $-\frac{1}{4}$. (Il faut faire attention au fait que le signe dans la formule pour le produit dépend de la parité de $n$.)
$$P(x) = c_n x^n + c_{n-1}x^{n-1} + \ldots + c_1 x + c_0$$ La deuxième fait intervenir les $n$ racines (comptées avec leur multiplicité) $r_1, r_2, \ldots, r_n$ de $P$ :
$$P(x) = c_n (x-r_1)(x-r_2)\ldots(x-r_n)$$ Puisqu'il s'agit de deux façons d'écrire un seul et même polynôme, on peut directement trouver des formules reliant les coefficients $c_i$ aux racines $r_i$. En effet, pour chaque $i \in \{0, 1, \ldots, n\}$, on peut calculer le coefficient de $x^i$ à partir de la deuxième forme et on sait qu'il doit être égal à $c_i$. Par exemple, pour $n = 3$, on peut développer la deuxième forme et obtenir
$$\begin{align}
P(x) &= c_3(x-r_1)(x-r_2)(x-r_3) \\
&= c_3(x^3 - (r_1+r_2+r_3)x^2 + (r_1r_2 + r_2r_3 + r_3r_1) x - r_1r_2r_3)
\end{align}$$ On en déduit que l'on a les formules (pour $n = 3$) :
$$\left\{ \begin{array}{l}
c_2 = -c_3 (r_1+r_2+r_3) \\[1mm]
c_1 = c_3 (r_1r_2 + r_2 r_3 + r_3r_1) \\[1mm]
c_0 = -c_3 (r_1r_2r_3)
\end{array}\right.
\quad \Leftrightarrow \quad
\left\{ \begin{array}{l}
r_1+r_2+r_3 = -\frac{c_2}{c_3}\\
r_1r_2 + r_2 r_3 + r_3r_1 = \frac{c_1}{c_3} \\
r_1r_2r_3 = -\frac{c_0}{c_3}
\end{array}\right.
$$ On peut effectuer le même raisonnement pour un polynôme de degré $n$, et on trouve les formules suivantes.
Formules de Viète
Soit un polynôme
$$P(x) = c_n x^n + c_{n-1} x^{n-1} + \ldots + c_1 x + c_0$$ à coefficients dans $\mathbb{C}$ et $r_1, r_2, \ldots, r_n$ les $n$ racines de $P$. On a
$$\left\{ \begin{array}{l}
r_1+r_2+\ldots + r_n = -\frac{c_{n-1}}{c_n}\\
r_1r_2 + r_1 r_3 + \ldots + r_1 r_n + r_2 r_3 + \ldots + r_{n-1}r_n = \frac{c_{n-2}}{c_n} \\
r_1r_2r_3 + r_1 r_2 r_4 + \ldots + r_1 r_2 r_n + r_1 r_3 r_4 + \ldots + r_{n-2} r_{n-1} r_n = -\frac{c_{n-3}}{c_n}\\
\quad \vdots \\
r_1r_2\ldots r_n = (-1)^n \cdot \frac{c_0}{c_n}
\end{array}\right.
$$ Autrement dit, pour tout $k \in \{1, \ldots, n\}$, la somme de tous les produits de $k$ racines est égale à $\displaystyle(-1)^k \cdot \frac{c_{n-k}}{c_n}$, ce que l'on peut encore écrire à l'aide d'un signe somme :
$$\sum_{i_1 < \ \ldots \ < i_k}r_{i_1} r_{i_2}\ldots r_{i_k} = (-1)^k \cdot \frac{c_{n-k}}{c_n}.$$
$$P(x) = c_n x^n + c_{n-1} x^{n-1} + \ldots + c_1 x + c_0$$ à coefficients dans $\mathbb{C}$ et $r_1, r_2, \ldots, r_n$ les $n$ racines de $P$. On a
$$\left\{ \begin{array}{l}
r_1+r_2+\ldots + r_n = -\frac{c_{n-1}}{c_n}\\
r_1r_2 + r_1 r_3 + \ldots + r_1 r_n + r_2 r_3 + \ldots + r_{n-1}r_n = \frac{c_{n-2}}{c_n} \\
r_1r_2r_3 + r_1 r_2 r_4 + \ldots + r_1 r_2 r_n + r_1 r_3 r_4 + \ldots + r_{n-2} r_{n-1} r_n = -\frac{c_{n-3}}{c_n}\\
\quad \vdots \\
r_1r_2\ldots r_n = (-1)^n \cdot \frac{c_0}{c_n}
\end{array}\right.
$$ Autrement dit, pour tout $k \in \{1, \ldots, n\}$, la somme de tous les produits de $k$ racines est égale à $\displaystyle(-1)^k \cdot \frac{c_{n-k}}{c_n}$, ce que l'on peut encore écrire à l'aide d'un signe somme :
$$\sum_{i_1 < \ \ldots \ < i_k}r_{i_1} r_{i_2}\ldots r_{i_k} = (-1)^k \cdot \frac{c_{n-k}}{c_n}.$$
Lorsqu'on est en présence d'un polynôme sous sa forme habituelle, on peut donc directement connaître la somme et le produit de ses racines en calculant $\displaystyle -\frac{c_{n-1}}{c_n}$ et $\displaystyle (-1)^n \cdot \frac{c_0}{c_n}$. On peut également connaître la somme de tous les produits de $k$ racines, ces formules étant plus rarement utilisées (mais il ne faut pas pour autant les oublier). En particulier, si le polynôme est unitaire, c'est-à-dire si $c_n = 1$, alors les coefficients donnent directement ces valeurs (au signe près).
Exemple : Soit $P(x) = 4x^5 - 3 x^4 + 2x^2 + 1$. La somme des $5$ racines de $P$ est égale à $\frac{3}{4}$ et le produit de celles-ci est égal à $-\frac{1}{4}$. (Il faut faire attention au fait que le signe dans la formule pour le produit dépend de la parité de $n$.)
2. Interpolation
Une question concernant les polynômes que l'on peut se poser est la suivante :
Le polynôme d'interpolation de Lagrange répond à cette question par l'affirmative. Non seulement on sait qu'un tel polynôme existe, mais on peut même le construire très facilement.
Évidemment, si on s'autorise un plus haut degré, alors il existe plusieurs polynômes (même une infinité) respectant $P(a_i) = b_i$ pour tout $i$. Cela dit, on essaye généralement d'avoir le plus petit degré possible, et c'est le polynôme d'interpolation de Lagrange qui nous le donne.
Remarque : Si les nombres $a_1, \ldots, a_n$ et $b_1, \ldots, b_n$ sont réels, alors le polynôme d'interpolation de Lagrange a également des coefficients réels, au vu de sa définition.
Exemple : Il est bien connu que pour tout $n \in \mathbb{N_0}$, on a $1+2+\ldots+n = \frac{n(n+1)}{2}$. On peut se demander s'il existe une telle formule pour la somme des premiers carrés $1^2 + 2^2 + \ldots + n^2$. On peut espérer qu'une telle formule existe et qu'elle prend la forme d'un polynôme $P$, comme $\frac{n(n+1)}{2}$. On sait que $P$ doit respecter
$$P(0) = 0, \ P(1) = 1, \ P(2) = 5, \ P(3) = 14, \ P(4) = 30, \ \ldots$$ On peut donc utiliser le polynôme d'interpolation de Lagrange avec quelques-unes de ces égalités pour obtenir un polynôme respectant celles-ci. Avec un peu de chance, le polynôme obtenu sera la formule désirée. Puisque la formule doit donner la somme des $n$ premiers carrés, on peut s'attendre à ce que le degré du polynôme soit supérieur à $2$. Il faut donc considérer au moins $4$ égalités $P(a_i) = b_i$ pour avoir une chance d'obtenir un polynôme $P$ de degré $3$. On va donc calculer le polynôme d'interpolation de Lagrange relatif aux quatre égalités
$$P(0) = 0, \ P(1) = 1, \ P(2) = 5, \ P(3) = 14.$$ La formule nous donne :
$$\begin{align}
P(x) & = 0 \cdot \frac{(x-1)(x-2)(x-3)}{(0-1)(0-2)(0-3)} + 1 \cdot \frac{(x-0)(x-2)(x-3)}{(1-0)(1-2)(1-3)} \\
& \quad +\ 5 \cdot \frac{(x-0)(x-1)(x-3)}{(2-0)(2-1)(2-3)} + 14 \cdot \frac{(x-0)(x-1)(x-2)}{(3-0)(3-1)(3-2)}\\[1mm]
&= \frac{x^3-5x^2+6x}{2} + \frac{5(x^3 -4x^2 + 3x)}{-2} + \frac{14(x^3-3x^2+2x)}{6} \\[1mm]
&= \frac{3x^3-15x^2+18x - 15x^3+60x^2 - 45x+14x^3-42x^2+28x}{6}\\[1mm]
& = \frac{2x^3 +3x^2+x}{6}\\[1mm]
& = \frac{x(x+1)(2x+1)}{6}
\end{align}$$ On peut vérifier que ce polynôme est bien la formule attendue (remarquons qu'on a bien $P(4) = 30$). En fait, il n'est pas difficile de montrer que la formule pour la somme des puissances $k$-èmes $1^k + 2^k + \ldots + n^k$ est toujours un polynôme de degré $k+1$. Dès lors, puisque le polynôme d'interpolation de Lagrange trouvé avec la méthode précédente est l'unique polynôme de degré inférieur ou égal à $k+1$ respectant les premières égalités, il s'agit forcément de la bonne formule.
À titre d'exercice, le lecteur peut calculer la formule donnant la somme des $n$ premiers cubes et remarquer que
$$1^3+2^3+\ldots + n^3 = (1+2+\ldots+n)^2.$$
Question
Étant donnés des complexes distincts $a_1, \ldots, a_n$ et des complexes $b_1, \ldots, b_n$, existe-t-il un polynôme $P \in \mathbb{C}[x]$ tel que $P(a_i) = b_i$ pour tout $i \in \{1, 2,\ldots, n\}$ ?
Le polynôme d'interpolation de Lagrange répond à cette question par l'affirmative. Non seulement on sait qu'un tel polynôme existe, mais on peut même le construire très facilement.
Théorème (polynôme d'interpolation de Lagrange)
Soit $n \in \mathbb{N}_0$, $a_1, \ldots, a_n$ des complexes distincts et $b_1, \ldots, b_n$ des complexes. Il existe un unique polynôme $P \in \mathbb{C}[x]$ de degré inférieur ou égal à $n-1$ et tel que $P(a_i) = b_i$ pour tout $i \in \{1, 2, \ldots, n\}$. On l'appelle le polynôme d'interpolation de Lagrange, et il s'explicite de la manière suivante :
$$P(x) = \sum_{i=1}^n \left( b_i \cdot \prod_{j \neq i} \frac{x-a_j}{a_i-a_j}\right).$$
$$P(x) = \sum_{i=1}^n \left( b_i \cdot \prod_{j \neq i} \frac{x-a_j}{a_i-a_j}\right).$$
Démonstration
Montrons que ce polynôme $P$ explicité ci-dessus convient. En fait, on se rend compte que pour tout $i$, le polynôme
$$P_i(x) := \prod_{j \neq i} \frac{x-a_j}{a_i-a_j} = \frac{(x-a_1)\ldots (x-a_{i-1})(x-a_{i+1}) \ldots (x-a_n)}{(a_i-a_1)\ldots (a_i-a_{i-1})(a_i-a_{i+1}) \ldots (a_i-a_n)}$$ est de degré $n-1$ et a été construit tel que $P_i(a_i) = 1$ et $P_i(a_j) = 0$ pour tout $j \neq i$. Ainsi, en prenant
$$P(x) = \sum_{i = 1}^n b_i \cdot P_i(x),$$ on a bien $P(a_i) = b_i$ pour tout $i \in \{1, 2, \ldots, n\}$ comme voulu, ainsi que $\deg P \leq n-1$ puisqu'en ajoutant des polynômes de degré $m$, on obtient toujours un polynôme de degré inférieur ou égal à $m$ (il se peut que les termes de plus haut degré s'annulent et que le degré baisse).
$$P_i(x) := \prod_{j \neq i} \frac{x-a_j}{a_i-a_j} = \frac{(x-a_1)\ldots (x-a_{i-1})(x-a_{i+1}) \ldots (x-a_n)}{(a_i-a_1)\ldots (a_i-a_{i-1})(a_i-a_{i+1}) \ldots (a_i-a_n)}$$ est de degré $n-1$ et a été construit tel que $P_i(a_i) = 1$ et $P_i(a_j) = 0$ pour tout $j \neq i$. Ainsi, en prenant
$$P(x) = \sum_{i = 1}^n b_i \cdot P_i(x),$$ on a bien $P(a_i) = b_i$ pour tout $i \in \{1, 2, \ldots, n\}$ comme voulu, ainsi que $\deg P \leq n-1$ puisqu'en ajoutant des polynômes de degré $m$, on obtient toujours un polynôme de degré inférieur ou égal à $m$ (il se peut que les termes de plus haut degré s'annulent et que le degré baisse).
Évidemment, si on s'autorise un plus haut degré, alors il existe plusieurs polynômes (même une infinité) respectant $P(a_i) = b_i$ pour tout $i$. Cela dit, on essaye généralement d'avoir le plus petit degré possible, et c'est le polynôme d'interpolation de Lagrange qui nous le donne.
Remarque : Si les nombres $a_1, \ldots, a_n$ et $b_1, \ldots, b_n$ sont réels, alors le polynôme d'interpolation de Lagrange a également des coefficients réels, au vu de sa définition.
Exemple : Il est bien connu que pour tout $n \in \mathbb{N_0}$, on a $1+2+\ldots+n = \frac{n(n+1)}{2}$. On peut se demander s'il existe une telle formule pour la somme des premiers carrés $1^2 + 2^2 + \ldots + n^2$. On peut espérer qu'une telle formule existe et qu'elle prend la forme d'un polynôme $P$, comme $\frac{n(n+1)}{2}$. On sait que $P$ doit respecter
$$P(0) = 0, \ P(1) = 1, \ P(2) = 5, \ P(3) = 14, \ P(4) = 30, \ \ldots$$ On peut donc utiliser le polynôme d'interpolation de Lagrange avec quelques-unes de ces égalités pour obtenir un polynôme respectant celles-ci. Avec un peu de chance, le polynôme obtenu sera la formule désirée. Puisque la formule doit donner la somme des $n$ premiers carrés, on peut s'attendre à ce que le degré du polynôme soit supérieur à $2$. Il faut donc considérer au moins $4$ égalités $P(a_i) = b_i$ pour avoir une chance d'obtenir un polynôme $P$ de degré $3$. On va donc calculer le polynôme d'interpolation de Lagrange relatif aux quatre égalités
$$P(0) = 0, \ P(1) = 1, \ P(2) = 5, \ P(3) = 14.$$ La formule nous donne :
$$\begin{align}
P(x) & = 0 \cdot \frac{(x-1)(x-2)(x-3)}{(0-1)(0-2)(0-3)} + 1 \cdot \frac{(x-0)(x-2)(x-3)}{(1-0)(1-2)(1-3)} \\
& \quad +\ 5 \cdot \frac{(x-0)(x-1)(x-3)}{(2-0)(2-1)(2-3)} + 14 \cdot \frac{(x-0)(x-1)(x-2)}{(3-0)(3-1)(3-2)}\\[1mm]
&= \frac{x^3-5x^2+6x}{2} + \frac{5(x^3 -4x^2 + 3x)}{-2} + \frac{14(x^3-3x^2+2x)}{6} \\[1mm]
&= \frac{3x^3-15x^2+18x - 15x^3+60x^2 - 45x+14x^3-42x^2+28x}{6}\\[1mm]
& = \frac{2x^3 +3x^2+x}{6}\\[1mm]
& = \frac{x(x+1)(2x+1)}{6}
\end{align}$$ On peut vérifier que ce polynôme est bien la formule attendue (remarquons qu'on a bien $P(4) = 30$). En fait, il n'est pas difficile de montrer que la formule pour la somme des puissances $k$-èmes $1^k + 2^k + \ldots + n^k$ est toujours un polynôme de degré $k+1$. Dès lors, puisque le polynôme d'interpolation de Lagrange trouvé avec la méthode précédente est l'unique polynôme de degré inférieur ou égal à $k+1$ respectant les premières égalités, il s'agit forcément de la bonne formule.
À titre d'exercice, le lecteur peut calculer la formule donnant la somme des $n$ premiers cubes et remarquer que
$$1^3+2^3+\ldots + n^3 = (1+2+\ldots+n)^2.$$
3. Formule de Taylor
Lorsqu'on est en présence d'un polynôme $P$ de $A[x]$ et qu'un certain $a \in A$ est une valeur que l'on désire privilégier, il peut être utile de ne plus écrire notre polynôme sous la forme usuelle
$$P(x) = c_n x^n + c_{n-1} x^{n-1} + \ldots + c_1 x + c_0,$$ mais plutôt sous une forme du type
$$P(x) = c'_n (x-a)^n + c'_{n-1} (x-a)^{n-1} + \ldots + c'_1 (x-a) + c'_0.$$ La formule de Taylor nous donne en fait une façon d'exprimer les coefficients $c'_i$ à partir des valeurs en $a$ des différents polynômes dérivés de $P$.
Remarquons que $\displaystyle \frac{P^{(n)}(a)}{n!}$ est toujours égal à $c_n$, le coefficient dominant de $P$, d'où $c'_n = c_n$ ce qui est parfaitement logique.
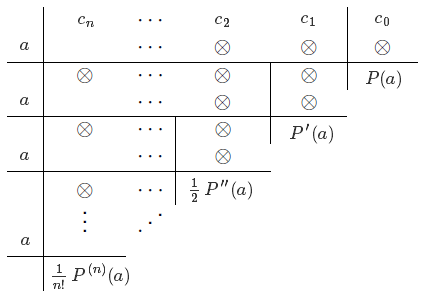
Il est en fait possible d'obtenir les valeurs des coefficients $c'_k$ en itérant le schéma de Horner. En effet, nous avons vu qu'en utilisant celui-ci pour diviser $P$ par $(x-a)$, la dernière valeur du tableau obtenue sera le reste de la division, à savoir $P(a)$. On peut alors recommencer en divisant le quotient obtenu $Q$ par $(x-a)$ et le reste obtenu sera exactement $c'_1 = P'(a)$. On continue ainsi de suite, et le reste à chaque étape sera exactement le coefficient suivant de la formule de Taylor.
$$P(x) = c_n x^n + c_{n-1} x^{n-1} + \ldots + c_1 x + c_0,$$ mais plutôt sous une forme du type
$$P(x) = c'_n (x-a)^n + c'_{n-1} (x-a)^{n-1} + \ldots + c'_1 (x-a) + c'_0.$$ La formule de Taylor nous donne en fait une façon d'exprimer les coefficients $c'_i$ à partir des valeurs en $a$ des différents polynômes dérivés de $P$.
Formule de Taylor
Soit $P \in A[x]$ un polynôme de degré $n$, et $a \in A$. On a
$$P(x) = \frac{P^{(n)}(a)}{n!} (x-a)^n + \frac{P^{(n-1)}(a)}{(n-1)!} (x-a)^{n-1} + \ldots + P'(a) (x-a) + P(a).$$
$$P(x) = \frac{P^{(n)}(a)}{n!} (x-a)^n + \frac{P^{(n-1)}(a)}{(n-1)!} (x-a)^{n-1} + \ldots + P'(a) (x-a) + P(a).$$
Remarquons que $\displaystyle \frac{P^{(n)}(a)}{n!}$ est toujours égal à $c_n$, le coefficient dominant de $P$, d'où $c'_n = c_n$ ce qui est parfaitement logique.
Démonstration
On peut facilement se convaincre qu'il existe effectivement des coefficients $c'_i$ tels que
$$P(x) = c'_n (x-a)^n + c'_{n-1} (x-a)^{n-1} + \ldots + c'_1 (x-a) + c'_0.$$ En effet, on prend $c'_n = c_n$, puis on choisit $c'_{n-1}$ de sorte que le coefficient de $x^{n-1}$ soit correct, puis $c'_{n-2}$, et ainsi de suite jusque $c'_0$. Il reste donc uniquement à exprimer chaque $c'_i$ en fonction des polynômes dérivés. Pour cela, on commence à évaluer $P$ en $a$ et on remarque que
$$P(a) = c'_n (a-a)^n + c'_{n-1} (a-a)^{n-1} + \ldots + c'_1 (a-a) + c'_0,$$ ce qui montre que $c'_0 = P(a)$. On calcule ensuite
$$P'(x) = nc'_n (x-a)^{n-1} + (n-1)c'_{n-1} (x-a)^{n-2} + \ldots + 2c'_2(x-a)+ c'_1,$$ et en évaluant $P'$ en $a$ on voit que $P'(a) = c'_1$. En continuant de la sorte, on verra que $P''(a) = 2c'_2$, puis $P^{(3)}(a) = 3\cdot2 \cdot c'_3$, et ainsi de suite. On obtient en fait à chaque étape la formule attendue
$$c'_k = \frac{P^{(k)}(a)}{k!}.$$
$$P(x) = c'_n (x-a)^n + c'_{n-1} (x-a)^{n-1} + \ldots + c'_1 (x-a) + c'_0.$$ En effet, on prend $c'_n = c_n$, puis on choisit $c'_{n-1}$ de sorte que le coefficient de $x^{n-1}$ soit correct, puis $c'_{n-2}$, et ainsi de suite jusque $c'_0$. Il reste donc uniquement à exprimer chaque $c'_i$ en fonction des polynômes dérivés. Pour cela, on commence à évaluer $P$ en $a$ et on remarque que
$$P(a) = c'_n (a-a)^n + c'_{n-1} (a-a)^{n-1} + \ldots + c'_1 (a-a) + c'_0,$$ ce qui montre que $c'_0 = P(a)$. On calcule ensuite
$$P'(x) = nc'_n (x-a)^{n-1} + (n-1)c'_{n-1} (x-a)^{n-2} + \ldots + 2c'_2(x-a)+ c'_1,$$ et en évaluant $P'$ en $a$ on voit que $P'(a) = c'_1$. En continuant de la sorte, on verra que $P''(a) = 2c'_2$, puis $P^{(3)}(a) = 3\cdot2 \cdot c'_3$, et ainsi de suite. On obtient en fait à chaque étape la formule attendue
$$c'_k = \frac{P^{(k)}(a)}{k!}.$$
Il est en fait possible d'obtenir les valeurs des coefficients $c'_k$ en itérant le schéma de Horner. En effet, nous avons vu qu'en utilisant celui-ci pour diviser $P$ par $(x-a)$, la dernière valeur du tableau obtenue sera le reste de la division, à savoir $P(a)$. On peut alors recommencer en divisant le quotient obtenu $Q$ par $(x-a)$ et le reste obtenu sera exactement $c'_1 = P'(a)$. On continue ainsi de suite, et le reste à chaque étape sera exactement le coefficient suivant de la formule de Taylor.

4. Irréductibilité
Définition
Pourvu que $A$ soit un anneau intègre, c'est-à-dire si le produit de deux éléments non nuls de $A$ n'est jamais nul, alors on dit qu'un polynôme $P \in A[x]$ est irréductible s'il est de degré au moins $1$ et si la seule façon d'avoir $P = QR$ avec $Q, R \in A[x]$ est que l'un des deux polynômes $Q$ et $R$ soit une constante (c'est-à-dire de degré $0$).Cette notion dépend fortement de l'anneau (intègre) $A$ sur lequel on considère le polynôme. Par exemple, le théorème fondamental de l'algèbre nous apprend que les seuls polynômes de $\mathbb{C}[x]$ qui sont irréductibles sont ceux de degré $1$. En effet, tous les polynômes de degré supérieur peuvent être décomposés en produit des $(x-r_i)$, c'est-à-dire en produit de polynômes non constants.
Dans $\mathbb{R}[x]$ par contre, au vu du résultat analogue au théorème fondamental pour les polynômes à coefficients réels, les seuls polynômes irréductibles sont ceux de degré $1$ et ceux de degré $2$ dont le discriminant $\Delta$ est strictement négatif.
Nous connaissons donc les polynômes irréductibles de $\mathbb{C}[x]$ et $\mathbb{R}[x]$. Il n'existe par contre pas de telle caractérisation des polynômes irréductibles de $\mathbb{Q}[x]$ ou $\mathbb{Z}[x]$, et la section suivante a pour but de donner des méthodes pour traiter ces cas.
Polynômes à coefficients entiers ou rationnels
Si on est en présence d'un polynôme de $\mathbb{Q}[x]$, c'est-à-dire à coefficients rationnels, on peut multiplier le polynôme par le plus petit commun multiple des dénominateurs des coefficients pour se ramener à un polynôme à coefficients entiers. Il semble donc que l'on puisse aisément passer de $\mathbb{Q}[x]$ à $\mathbb{Z}[x]$, mais il faut tout de même faire attention : on pourrait peut-être avoir un polynôme à coefficients entiers qui soit irréductible dans $\mathbb{Z}[x]$ mais réductible dans $\mathbb{Q}[x]$. Le lemme de Gauss suivant nous indique en fait que ce n'est jamais le cas.Lemme de Gauss
Si $P \in \mathbb{Z}[x]$ est réductible dans $\mathbb{Q}[x]$, alors il l'est également dans $\mathbb{Z}[x]$.
Démonstration
Commençons par prouver qu'étant donné un polynôme non-nul $Q \in \mathbb{Q}[x]$, il existe toujours $\alpha \in \mathbb Q_0^+$ tel que $\alpha \cdot Q$ ait ses coefficients entiers et premiers entre eux. C'est en fait assez évident : on peut commencer par multiplier $Q$ par le plus petit commun multiple $d$ des dénominateurs de tous ses coefficients, pour obtenir $d\cdot Q$ à coefficients entiers. On divise ensuite $d\cdot Q$ par le plus grand commun diviseur $n$ de tous ses coefficients pour obtenir $\frac{d}{n} \cdot Q$ dont les coefficients sont toujours entiers, mais cette fois également premiers entre eux.
Considérons maintenant un polynôme non-nul $P \in \mathbb{Z}[x]$ réductible dans $\mathbb{Q}[x]$, c'est-à-dire qu'on a $P = Q\cdot R$ avec $Q, R\in\mathbb{Q}[x]$. En appliquant notre résultat préliminaire à $Q$ et $R$ séparément, on obtient $\alpha, \beta \in \mathbb{Q}_0^+$ tels que $Q' = \alpha \cdot Q$ et $R' = \beta \cdot R$ ont leurs coefficients entiers et premiers entre eux. Quitte à noter $\alpha \beta = \frac{a}{b}$ avec $a, b > 0$ et $\mathrm{pgcd}(a,b) = 1$, on a donc $a \cdot P = b\cdot Q' \cdot R'$ avec $Q', R' \in \mathbb{Z}[x]$. Pour conclure que $P$ est bien réductible sur $\mathbb{Z}[x]$, il ne reste plus qu'à montrer que $a = 1$.
Procédons par l'absurde, en supposant que $a \ne 1$. Il existe donc $p$ premier tel que $p \mid a$. Vu que $\mathrm{pgcd}(a,b) = 1$, il vient que le polynôme $Q' \cdot R'$ a tous ses coefficients divisibles par $p$. Notons $q_i$ (respectivement $r_i$) le coefficient de $x^i$ dans $Q'$ (respectivement $R'$). On sait que $Q'$ et $R'$ ont chacun leurs coefficients premiers entre eux, donc il existe $s, t \ge 0$ tels que $p \not \mid q_s$ et $p \not \mid r_t$. On choisit $s$ et $t$ minimaux, c'est-à-dire tels que $p \mid q_0, \ldots, q_{s-1}$ et $p \mid r_0, \ldots, r_{t-1}$. Le coefficient de $x^{s+t}$ dans $Q' \cdot R'$ est donné par la somme
$$q_0 r_{s+t} + q_1 r_{s+t-1} + \ldots + q_{s-1} r_{t+1} + q_s r_t + q_{s+1} r_{t-1} + \ldots + q_{s+t-1} r_1 + q_{s+t} r_0,$$ dont tous les termes sont divisibles par $p$ à l'exception de $q_s r_t$. Ce coefficient n'est donc pas divisible par $p$, contrairement à ce qui avait été établi.
Considérons maintenant un polynôme non-nul $P \in \mathbb{Z}[x]$ réductible dans $\mathbb{Q}[x]$, c'est-à-dire qu'on a $P = Q\cdot R$ avec $Q, R\in\mathbb{Q}[x]$. En appliquant notre résultat préliminaire à $Q$ et $R$ séparément, on obtient $\alpha, \beta \in \mathbb{Q}_0^+$ tels que $Q' = \alpha \cdot Q$ et $R' = \beta \cdot R$ ont leurs coefficients entiers et premiers entre eux. Quitte à noter $\alpha \beta = \frac{a}{b}$ avec $a, b > 0$ et $\mathrm{pgcd}(a,b) = 1$, on a donc $a \cdot P = b\cdot Q' \cdot R'$ avec $Q', R' \in \mathbb{Z}[x]$. Pour conclure que $P$ est bien réductible sur $\mathbb{Z}[x]$, il ne reste plus qu'à montrer que $a = 1$.
Procédons par l'absurde, en supposant que $a \ne 1$. Il existe donc $p$ premier tel que $p \mid a$. Vu que $\mathrm{pgcd}(a,b) = 1$, il vient que le polynôme $Q' \cdot R'$ a tous ses coefficients divisibles par $p$. Notons $q_i$ (respectivement $r_i$) le coefficient de $x^i$ dans $Q'$ (respectivement $R'$). On sait que $Q'$ et $R'$ ont chacun leurs coefficients premiers entre eux, donc il existe $s, t \ge 0$ tels que $p \not \mid q_s$ et $p \not \mid r_t$. On choisit $s$ et $t$ minimaux, c'est-à-dire tels que $p \mid q_0, \ldots, q_{s-1}$ et $p \mid r_0, \ldots, r_{t-1}$. Le coefficient de $x^{s+t}$ dans $Q' \cdot R'$ est donné par la somme
$$q_0 r_{s+t} + q_1 r_{s+t-1} + \ldots + q_{s-1} r_{t+1} + q_s r_t + q_{s+1} r_{t-1} + \ldots + q_{s+t-1} r_1 + q_{s+t} r_0,$$ dont tous les termes sont divisibles par $p$ à l'exception de $q_s r_t$. Ce coefficient n'est donc pas divisible par $p$, contrairement à ce qui avait été établi.
Nous avons donc expliqué comment le fait d'être irréductible ou réductible dans $\mathbb{Q}[x]$ se ramène aisément au fait d'être irréductible ou réductible dans $\mathbb{Z}[x]$. Il reste maintenant à savoir détecter quand un polynôme de $\mathbb{Z}[x]$ est irréductible.
Il n'est malheureusement pas facile de voir si un polynôme de $\mathbb{Z}[x]$ est réductible ou non. Pour montrer qu'un polynôme $P$ est réductible, on peut bien sûr lui trouver une factorisation non triviale $P = QR$, mais montrer qu'il n'existe pas de telle factorisation est bien plus compliqué. Il ne faut déjà pas commettre l'erreur courante suivante : être irréductible n'est en général pas équivalent à ne pas avoir de racine ! En effet, il se peut qu'un polynôme n'ait pas de racines mais qu'il soit tout de même réductible, comme c'est par exemple le cas du polynôme
$$P(x) = (x^2+1)(x^2+4).$$ Ce polynôme est réductible vu qu'il se factorise, mais il n'a aucune racine entière puisque ses racines dans $\mathbb{C}$ sont $i$, $-i$, $2i$ et $-2i$. Il existe tout de même un cas où on peut se contenter de montrer qu'un polynôme n'a pas de racines entières pour montrer qu'il est irréductible : celui où le polynôme est unitaire et son degré est inférieur ou égal à $3$. En effet, dans ce cas toute factorisation non triviale du type $P = QR$ comprend un polynôme (unitaire) de degré $1$. Dans ce contexte, on peut donc simplement se contenter de prouver que $P$ n'a pas de racine entière, et on peut pour cela utiliser le résultat suivant (dont la démonstration est un simple exercice de théorie des nombres) :
Lemme
Soit $P \in \mathbb{Z}[x]$ un polynôme. Si $\frac{p}{q}$ est une racine rationnelle de $P$, avec $p$ et $q$ premiers entre eux, alors $p$ divise le terme indépendant de $P$ et $q$ divise son coefficient dominant.
En particulier, ce résultat nous indique que les seules racines entières éventuelles d'un tel polynôme divisent le terme indépendant du polynôme : on peut donc se contenter de tester tous les diviseurs (éventuellement négatifs) de ce terme indépendant.
Exemple : Le polynôme $P(x) = 2x^5 - x^2 + 3$ n'a que huit racines rationnelles possibles : $\pm 1$, $\pm 3$, $\pm\frac{1}{2}$, et $\pm\frac{3}{2}$. Il suffit de les tester et on voit notamment que $-1$ est une racine.
Si par contre, on est en présence d'un polynôme de degré supérieur ou égal à $4$, alors montrer qu'il n'existe pas de racines ne suffit plus. Une façon de faire, par exemple pour un polynôme de degré $4$, est d'en plus montrer qu'il ne se factorise pas en produit de deux polynômes de degré $2$. On peut procéder par l'absurde en supposant que le polynôme s'écrit comme
$$(ax^2 + bx + c)(d x^2 + ex + f)$$ et en trouvant des conditions sur $a, b, c, d, e$ et $f$ pour trouver une absurdité, mais un tel raisonnement devient vite long.
Une autre possibilité est d'utiliser le critère d'Eisenstein (qui se démontre aussi aisément par un peu de théorie des nombres) :
Critère d'Eisenstein
Soit $P(x) = c_n x^n + c_{n-1} x^{n-1} + \ldots + c_1 x + c_0$ un polynôme à coefficients entiers. S'il existe un nombre premier $p$ tel que
- $p$ divise $c_0, c_1, \ldots, c_{n-1}$ ;
- $p$ ne divise pas $c_n$ ;
- $p^2$ ne divise pas $c_0$,
Exemple : Le polynôme $x^5 - 4x^2 + 6x - 2$ est irréductible : les trois conditions sont respectées pour $p = 2$.
Quand le critère d'Eisenstein ne s'applique pas, on peut également effectuer un changement de variable du type $y = x+c$ (pour un certain $c \in \mathbb{Z}$) pour arriver à un autre polynôme auquel le critère s'applique éventuellement. En effet, le polynôme $P(x)$ est clairement irréductible si et seulement si $P(x-c)$ l'est.
Exemple : Le polynôme $P(x) = x^{p-1}+x^{p-2}+\ldots+x+1$ est irréductible pour $p$ premier. Pour le montrer, remarquons d'abord que $P$ peut s'écrire (il s'agit d'une formule bien connue) comme
$$P(x) = \frac{x^p-1}{x-1}.$$ Intéressons-nous à présent au polynôme $Q$ défini par $Q(x) = P(x+1)$. Montrer que $P$ est irréductible revient à montrer que $Q$ est irréductible. Or nous avons :
$$Q(x) = P(x+1) = \frac{(x+1)^p - 1}{x}.$$ Par la formule du binôme de Newton (voir combinatoire), on peut développer en
$$\begin{align}
Q(x) & = \frac{x^p + C^1_p x^{p-1} + C^2_p x^{p-2} + \ldots + C^{p-1}_p x +1 - 1}{x} \\[1mm]
&= x^{p-1} + C^1_p x^{p-2} + C^2_p x^{p-3} + \ldots + C^{p-1}_p
\end{align}$$ On peut alors directement utiliser le critère d'Eisenstein avec $p$, car $p$ divise tous les coefficients sauf le dominant (le nombre $C^k_p$ est toujours divisible par $p$ lorsque $p$ est premier et $1 \leq k \leq p-1$) et $p^2$ ne divise pas $C^{p-1}_p = p$.