Théorie > Algèbre > Nombres complexes (forme exponentielle)
Prérequis
Résumé
Multiplier deux nombres complexes ou élever un nombre complexe à une certaine puissance donne lieu à des formules peu attrayantes lorsqu'on utilise la forme habituelle $a+ib$. Nous présentons dans ce chapitre la forme trigonométrique et la forme exponentielle des nombres complexes, qui ont une interprétation géométrique et permettent de multiplier ou d'élever à une puissance de manière beaucoup plus efficace.
Ce chapitre a été écrit par N. Radu et mis en ligne le 8 décembre 2014.
1. Plan complexe
Comme tout nombre complexe peut simplement être considéré comme un couple de nombres réels (sa partie réelle et sa partie imaginaire), on peut penser à $\mathbb{C}$ comme à un plan usuel. On parle alors de plan complexe, et le nombre complexe $x+iy$ est considéré comme le point du plan de coordonnées $(x, y)$. L'axe des abscisses est alors appelé axe des réels puisque l'abscisse d'un point correspond à la partie réelle du nombre correspondant, alors que l'axe des ordonnées est appelé axe des imaginaires pour la même raison.
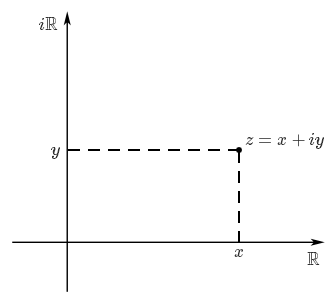
Sur ce plan, il est donc facile de visualiser la partie réelle et la partie imaginaire d'un complexe puisqu'il suffit de projeter le point correspondant sur l'axe voulu. En fait, il est aussi facile de trouver géométriquement le conjugué $\bar z$ d'un nombre complexe $z$, ainsi que son module $|z|$.
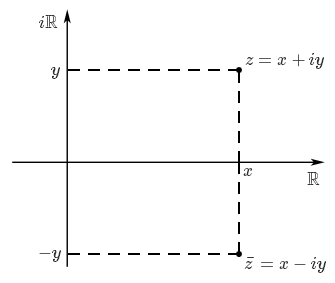
Puisque le conjugué de $z = x+iy$ est $\bar z = x-iy$, il s'agit géométriquement du point symétrique à $z$ par rapport à l'axe des abscisses, comme sur la figure suivante.
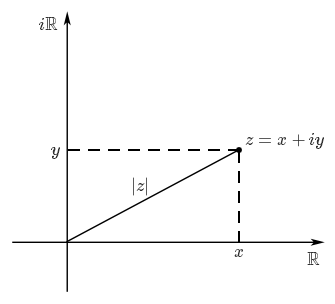
En ce qui concerne le module, on reconnait en la formule $|z| = \sqrt{x^2+y^2}$ la distance entre le point $(x, y)$ et l'origine $(0,0)$. Le module de nombre complexe est donc simplement la distance séparant le point correspondant à l'origine du plan complexe.

Sur ce plan, il est donc facile de visualiser la partie réelle et la partie imaginaire d'un complexe puisqu'il suffit de projeter le point correspondant sur l'axe voulu. En fait, il est aussi facile de trouver géométriquement le conjugué $\bar z$ d'un nombre complexe $z$, ainsi que son module $|z|$.
Puisque le conjugué de $z = x+iy$ est $\bar z = x-iy$, il s'agit géométriquement du point symétrique à $z$ par rapport à l'axe des abscisses, comme sur la figure suivante.

En ce qui concerne le module, on reconnait en la formule $|z| = \sqrt{x^2+y^2}$ la distance entre le point $(x, y)$ et l'origine $(0,0)$. Le module de nombre complexe est donc simplement la distance séparant le point correspondant à l'origine du plan complexe.

2. Forme trigonométrique
Argument
La représentation des complexes sur le plan peut nous inspirer une vision trigonométrique des nombres complexes. En effet, nous identifions pour le moment un nombre complexe par ses coordonnées cartésiennes $(x, y)$ dans le plan, mais il est aussi possible d'identifier un point $P$ du plan en donnant sa distance par rapport à l'origine $O$ et l'angle que fait $OP$ avec l'axe des abscisses (il s'agit des coordonnées polaires).On sait déjà, lorsque $z \in \mathbb{C}$, que la distance entre le point correspondant et l'origine est donnée par le module $|z|$ de $z$. On définit maintenant l'argument de $z$ (noté $\arg z$) comme étant l'angle déterminé par l'axe des abscisses (sa partie positive) et le segment reliant l'origine à $z$, comme indiqué sur la figure suivante. Cette définition n'a pas réellement de sens pour $z = 0$, c'est pourquoi on considérera toujours à présent des nombres complexes non nuls (sans forcément le mentionner).
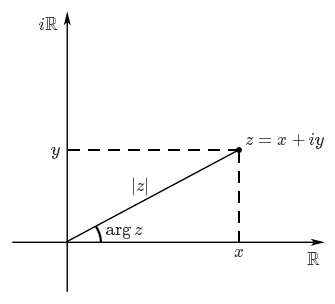
Il s'agit là d'une définition géométrique, mais on peut comme pour le module définir l'argument à partir de $x$ et $y$. Cette partie demande une familiarisation avec les fonctions trigonométriques inverses et n'est pas obligatoire.
Sur la figure précédente, on voit que la tangente de l'angle $\arg z$ est égale à $\displaystyle \frac{y}{x}$ (pourvu que $x$ soit non nul). En se rappelant que l'arctangente d'un nombre réel $x$ est défini comme l'angle de $\displaystyle\left] -\frac{\pi}{2}, \frac{\pi}{2}\right[$ dont la tangente vaut $x$, on peut donc donner la formule suivante pour l'argument de $z = x+iy$ :
$$\arg z = \left\{\begin{array}{cl}
\arctan \left(\frac{y}{x} \right) & \text{ si } \ x > 0, \\
\pi + \arctan \left(\frac{y}{x} \right) & \text{ si } \ x < 0, \\
\frac{\pi}{2} & \text{ si } \ x = 0 \ \text{ et } \ y > 0, \\[1mm]
-\frac{\pi}{2} & \text{ si } \ x = 0 \ \text{ et } \ y < 0.
\end{array}\right.$$ Cette définition est ici donnée à $2\pi$ près, en ce sens que l'angle $\pi$ est par exemple considéré comme identique à l'angle $3\pi$.
Forme trigonométrique des nombres complexes
Nous avons vu comment, à partir de $x$ et $y$, on peut trouver le module et l'argument de $z = x+iy$. Si maintenant, nous connaissons le module $r$ et l'argument $\theta$ d'un nombre complexe $z$, alors on peut retrouver sa forme habituelle $z = x+iy$. En effet, on voit aisément sur la figure précédente que$$\left\{\begin{array}{l}
x = |z| \cdot \cos (\arg z) = r \cos \theta, \\
y = |z| \cdot \sin (\arg z) = r \sin \theta.
\end{array}\right.$$ On dit qu'un nombre complexe $z$ est sous sa forme trigonométrique lorsqu'on l'écrit
$$z = r \cos \theta + i \cdot r \sin \theta = r(\cos \theta + i \sin \theta).$$ Par exemple, le nombre complexe $z = \sqrt{3} - i$ s'écrit sous forme trigonométrique comme
$$z = 2\left(\cos\left(\frac{-\pi}{6}\right) + i \sin \left(\frac{-\pi}{6}\right)\right),$$ puisque son module vaut $\sqrt{\left(\sqrt{3}\right)^2 + (-1)^2} = 2$ et la tangente de son argument vaut $\displaystyle\frac{-1}{\sqrt{3}} = \frac{-\sqrt{3}}{3}$ : on reconnaît la tangente de l'angle $\displaystyle\frac{-\pi}{6}$.
3. Forme exponentielle
Propriété de l'argument
La forme trigonométrique des nombres complexes peut sembler peu pratique. En effet, si $z = r(\cos \theta + i \sin \theta)$ et $z' = r'(\cos\theta' + i\sin \theta')$, alors il ne semble pas évident de trouver la forme trigonométrique de $z+z'$. On a bien$$z + z' = (r \cos \theta + r' \cos \theta') + i(r \sin \theta + r' \sin \theta'),$$ et on peut calculer le module et l'argument de cette somme, mais il ne s'agira pas d'une formule intéressante.
En fait, la forme trigonométrique se révèle très pratique lorsqu'on désire multiplier des nombres complexes. Si on a $z = r(\cos \theta + i \sin \theta)$ et $z' = r'(\cos\theta' + i\sin \theta')$, on trouve effectivement
$$\begin{align}
z\cdot z' &= r(\cos \theta + i \sin \theta)\cdot r'(\cos \theta' + i \sin \theta') \\
&= rr'\left(\cos\theta \cos \theta' - \sin \theta \sin \theta' + i(\cos \theta \sin \theta' + \sin \theta \cos \theta')\right) \\
&= rr'\left(\cos(\theta+\theta') + i \sin (\theta + \theta') \right)
\end{align}$$ On trouve directement la forme trigonométrique du produit de $z$ et $z'$ ! Son module est $rr'$ et son argument $\theta+\theta'$, ce qui signifie que le module d'un produit est égal au produit des modules (nous avions déjà donné cette propriété) et que l'argument d'un produit est égal à la somme des arguments :
$$\arg(z \cdot z') = \arg z + \arg z'.$$
Forme exponentielle des nombres complexes
La dernière formule trouvée pour l'argument d'un produit n'est pas sans rappeler les exponentielles, puisque le produit de deux exponentielles est égal à l'exponentielle de la somme. C'est pour cette raison que l'on introduit la notation suivante :$$e^{i \theta} = \cos \theta + i \sin \theta.$$ Il ne faut pas ici s'effrayer face à l'exponentielle : il ne s'agit que d'une notation. Historiquement, cette dernière égalité est en fait plutôt connue comme la formule d'Euler. En effet, il est possible de définir une exponentielle complexe $e^{ix}$ d'une façon totalement indépendante des fonctions trigonométriques, et la formule d'Euler donne alors une relation étonnante entre l'exponentielle et les fonctions trigonométriques. Cela n'est cependant pas notre point de vue, et il faut juste retenir qu'il s'agit d'une nouvelle notation.
Un cas particulier de la formule d'Euler est l'identité d'Euler bien connue suivante :
$$e^{i\pi} + 1 = 0$$ Encore une fois, cette identité peut sembler bien anodine au vu de notre définition de $e^{i \theta}$ comme une notation, mais il y a derrière elle quelque chose de bien plus fondamental. Cette identité est impressionnante de par le fait qu'elle relie les valeurs fondamentales $e$, $i$ et $\pi$ a priori indépendantes à l'aide des trois opérations arithmétiques d'addition, multiplication et exponentiation.
Au vu de la forme trigonométrique, on peut maintenant écrire un nombre complexe de module $r$ et d'argument $\theta$ comme
$$z = r \cdot e^{i \theta}.$$ Pour reprendre l'exemple donné précédemment, on a $\sqrt{3}-i = 2\cdot e^{-i\frac{\pi}{6}}$.
Multiplication sous forme exponentielle
Alors que multiplier deux nombres complexes sous la forme usuelle donnait lieu à des formules compliquées, la multiplication est un jeu d'enfant sous la forme exponentielle. On a en effet$$\left(r \cdot e^{i \theta}\right)\cdot \left(r' \cdot e^{i \theta'}\right) = rr' \cdot e^{i(\theta + \theta')}.$$ Cette formule nous donne aussi directement l'inverse d'un nombre complexe $r \cdot e^{i \theta}$, puisqu'il faut avoir $rr' = 1$ et $\theta+\theta' = 0$. On a ainsi
$$\frac{1}{r \cdot e^{i \theta}} = \frac{1}{r} \cdot e^{-i\theta}.$$ On peut maintenant voir comment, sur le plan complexe, on peut construire le produit de deux nombres complexes. Pour effectuer la somme de $z$ et $z'$, il suffit de prendre la somme des vecteurs $\vec{OZ}$ et $\vec{OZ'}$ où $Z$ et $Z'$ sont les points du plan représentant $z$ et $z'$. L'interprétation est un peu plus compliquée pour le produit. On note $U$ le point de coordonnées $(1,0)$, c'est-à-dire celui associé au nombre complexe $1$. Alors le point $P$ correspondant au produit de $z$ et $z'$ est tel que les triangles $OZ'P$ et $OUZ$ sont semblables, comme sur la figure suivante.
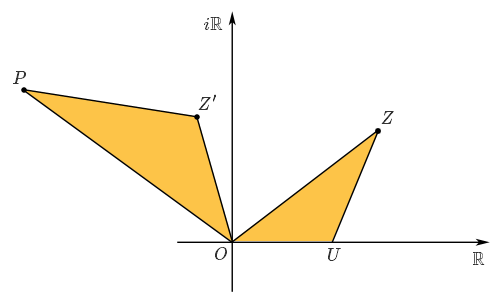
En effet, puisque $\arg(z\cdot z') = \arg z + \arg z'$, on a $\widehat{UOP} = \widehat{UOZ} + \widehat{UOZ'}$, d'où on déduit $\widehat{Z'OP} = \widehat{UOZ}$. Les deux triangles sont alors semblables puisqu'on a également
$$\frac{|OP|}{|OZ'|} = \frac{|z \cdot z'|}{|z'|} = |z| = \frac{|z|}{|1|} = \frac{|OZ|}{|OU|}.$$
Multiplier par $r \cdot e^{i \theta}$ revient en fait à effectuer une rotation d'angle $\theta$ ainsi qu'une homothétie de rapport $r$ (avec l'origine pour centre).
4. Racines $n$-èmes
Nous avons vu que multiplier deux nombres complexes est plus simple sous la forme exponentielle. En particulier, on peut facilement élever un nombre complexe à la puissance $n$ puisqu'on a simplement
$$\left(r \cdot e^{i \theta} \right)^n = r^n \cdot e^{in\theta}.$$ Réciproquement, cela permet d'extraire les racines $n$-èmes d'un nombre complexe très facilement, alors que nous avons vu précédemment qu'extraire une racine carrée était déjà fastidieux sous la forme usuelle. Pour le voir, considérons un nombre complexe non nul $c = r\cdot e^{i \theta}$ et cherchons quelles sont ses racines $n$-èmes. Un nombre $z = s \cdot e^{i \varphi}$ (de module $s$ et d'argument $\varphi$) est racine $n$-ème de $c$ si et seulement si sa $n$-ème puissance vaut $c$, c'est-à-dire si
$$s^n \cdot e^{in\varphi} = r \cdot e^{i\theta}.$$ Les modules doivent être égaux donc $s = \sqrt[n]{r}$, et les arguments aussi d'où $n\varphi = \theta$. Cette dernière égalité n'est cependant pas tout à fait correcte. En effet, nous avons mentionné que nous considérions des angles comme égaux dès qu'ils étaient égaux à un multiple de $2\pi$ près. Il ne faut donc pas avoir $n\varphi = \theta$, mais plutôt $n \varphi = \theta + 2k \pi$ pour un certain $k \in \mathbb{Z}$. Les racines $n$-èmes de $c = r \cdot e^{i \theta}$ sont donc les nombres complexes de la forme (on note $\exp$ au lieu de $e$ pour des raisons pratiques)
$$z_k = \sqrt[n]{r} \cdot \exp\left(i\left(\frac{\theta}{n} + \frac{2k\pi}{n}\right)\right)$$ avec $k \in \mathbb{Z}$. En fait, on voit aisément qu'il n'y a pas une infinité de racines mais exactement $n$, car la valeur de cette expression pour $k = n$ est la même que celle pour $k = 0$. Tout nombre complexe non nul possède donc exactement $n$ racines $n$-èmes, en prenant par exemple $z_0, \ldots, z_{n-1}$.
En particulier, les racines $n$-èmes de $1$ sont les nombres complexes
$$w_k = \exp\left( \frac{2ik\pi}{n} \right) = \cos\left( \frac{2k\pi}{n} \right) + i \sin \left( \frac{2k\pi}{n} \right)$$ pour $k \in \{0, 1, \ldots, n-1\}$. Notez que la valeur de $w_k$ dépend bel et bien de $n$, même si la notation ne l'indique pas ! Pour $k = 0$, on retrouve $w_0 = 1$, alors que quand $n$ est pair, on retrouve $w_{\frac{n}{2}} = e^{i \pi} = -1$ ce qui est logique puisque $-1$ est bien une racine $n$-ème de $1$ lorsque $n$ est pair. L'ensemble des racines $n$-èmes de l'unité est donc l'ensemble des sommets du $n$-gone centré en l'origine et ayant $1$ pour sommet. Sur la figure suivante, les racines $6$-èmes de l'unité sont représentées.
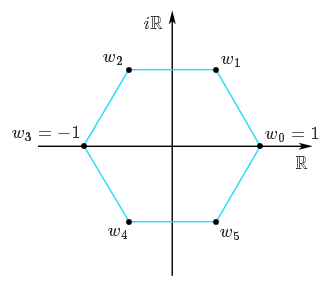
Les racines de l'unité sont intéressantes car, dès que l'on connait une racine $n$-ème d'un complexe non nul $c$, on peut trouver toutes les autres en la multipliant par les différentes racines $n$-èmes de $1$.
$$\left(r \cdot e^{i \theta} \right)^n = r^n \cdot e^{in\theta}.$$ Réciproquement, cela permet d'extraire les racines $n$-èmes d'un nombre complexe très facilement, alors que nous avons vu précédemment qu'extraire une racine carrée était déjà fastidieux sous la forme usuelle. Pour le voir, considérons un nombre complexe non nul $c = r\cdot e^{i \theta}$ et cherchons quelles sont ses racines $n$-èmes. Un nombre $z = s \cdot e^{i \varphi}$ (de module $s$ et d'argument $\varphi$) est racine $n$-ème de $c$ si et seulement si sa $n$-ème puissance vaut $c$, c'est-à-dire si
$$s^n \cdot e^{in\varphi} = r \cdot e^{i\theta}.$$ Les modules doivent être égaux donc $s = \sqrt[n]{r}$, et les arguments aussi d'où $n\varphi = \theta$. Cette dernière égalité n'est cependant pas tout à fait correcte. En effet, nous avons mentionné que nous considérions des angles comme égaux dès qu'ils étaient égaux à un multiple de $2\pi$ près. Il ne faut donc pas avoir $n\varphi = \theta$, mais plutôt $n \varphi = \theta + 2k \pi$ pour un certain $k \in \mathbb{Z}$. Les racines $n$-èmes de $c = r \cdot e^{i \theta}$ sont donc les nombres complexes de la forme (on note $\exp$ au lieu de $e$ pour des raisons pratiques)
$$z_k = \sqrt[n]{r} \cdot \exp\left(i\left(\frac{\theta}{n} + \frac{2k\pi}{n}\right)\right)$$ avec $k \in \mathbb{Z}$. En fait, on voit aisément qu'il n'y a pas une infinité de racines mais exactement $n$, car la valeur de cette expression pour $k = n$ est la même que celle pour $k = 0$. Tout nombre complexe non nul possède donc exactement $n$ racines $n$-èmes, en prenant par exemple $z_0, \ldots, z_{n-1}$.
Interprétation géométrique
Regardons finalement comment construire les différentes racines $n$-èmes d'un nombre complexe sur le plan complexe. Si on considère la racine obtenue avec $k = 0$, celle-ci s'obtient simplement en prenant la racine $n$-ème du module et en divisant l'argument par $n$. Ensuite, les autres racines s'obtiennent simplement en augmentant l'argument d'un multiple de $\displaystyle \frac{2\pi}{n}$, c'est-à-dire en effectuant une rotation de cet angle. Les racines $n$-èmes d'un complexe sont donc toujours les sommets d'un $n$-gône régulier.En particulier, les racines $n$-èmes de $1$ sont les nombres complexes
$$w_k = \exp\left( \frac{2ik\pi}{n} \right) = \cos\left( \frac{2k\pi}{n} \right) + i \sin \left( \frac{2k\pi}{n} \right)$$ pour $k \in \{0, 1, \ldots, n-1\}$. Notez que la valeur de $w_k$ dépend bel et bien de $n$, même si la notation ne l'indique pas ! Pour $k = 0$, on retrouve $w_0 = 1$, alors que quand $n$ est pair, on retrouve $w_{\frac{n}{2}} = e^{i \pi} = -1$ ce qui est logique puisque $-1$ est bien une racine $n$-ème de $1$ lorsque $n$ est pair. L'ensemble des racines $n$-èmes de l'unité est donc l'ensemble des sommets du $n$-gone centré en l'origine et ayant $1$ pour sommet. Sur la figure suivante, les racines $6$-èmes de l'unité sont représentées.

Les racines de l'unité sont intéressantes car, dès que l'on connait une racine $n$-ème d'un complexe non nul $c$, on peut trouver toutes les autres en la multipliant par les différentes racines $n$-èmes de $1$.