Théorie > Fondements > Trigonométrie
Prérequis
Aucun prérequis.
Résumé
Les fonctions trigonométriques $\sin$, $\cos$, $\tan$ et $\mathrm{cotan}$ sont fondamentales en géométrie. Nous rappelons ici les définitions de ces fonctions ainsi que toutes les formules permettant de simplifier et résoudre des équations trigonométriques, comme les formules de duplication, de Carnot ou encore de Simpson. Les définitions des fonctions trigonométriques inverses $\arcsin$, $\arccos$ et $\arctan$ sont également données.
Ce chapitre a été écrit par N. Radu et mis en ligne le 8 décembre 2014.
1. Degrés et radians
L'unité la plus connue pour la mesure des angles est le degré : un angle droit mesure $90^\circ$, un angle plat mesure $180^\circ$, et un cercle est divisé en $360^\circ$. Il existe cependant une autre unité pour mesurer les angles : le radian. L'idée derrière le radian est que, si on considère un cercle unité (c'est-à-dire de rayon $1$) de centre $O$, alors l'amplitude en radian d'un certain angle $\widehat{AOB}$ avec $A$ et $B$ sur le cercle est exactement égale à la longueur de l'arc que l'angle intercepte.
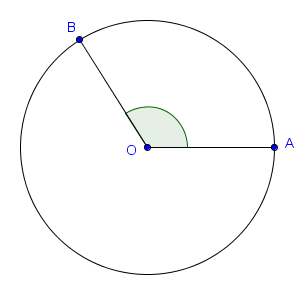
Puisque la circonférence du cercle unité est égale à $2\pi$, on en déduit qu'un angle de $360^\circ$ est de mesure $2 \pi$ radians. Ce qui relie les degrés et les radians est donc l'égalité :
$$\pi \text{ radians} = 180^\circ.$$ Lorsqu'on exprime un angle en radians, on ne note généralement pas l'unité. On dira par exemple qu'un angle droit a une amplitude de $\frac{\pi}{2}$.

Puisque la circonférence du cercle unité est égale à $2\pi$, on en déduit qu'un angle de $360^\circ$ est de mesure $2 \pi$ radians. Ce qui relie les degrés et les radians est donc l'égalité :
$$\pi \text{ radians} = 180^\circ.$$ Lorsqu'on exprime un angle en radians, on ne note généralement pas l'unité. On dira par exemple qu'un angle droit a une amplitude de $\frac{\pi}{2}$.
2. Fonctions trigonométriques
Fonctions sinus et cosinus
Étant donné un angle $\theta$, on peut lui associer un sinus et un cosinus. Pour définir ceux-ci, on représente l'angle $\theta$ dans le cercle unité centré en l'origine d'un repère orthonormé. Si $O$ est l'origine et $A$ le point de coordonnées $(1, 0)$, on prend $P$ le point du cercle tel que $\widehat{AOP} = \theta$. Il faut faire attention que l'on mesure ici les angles de manières orientées, dans le sens trigonométrique. Cela signifie que pour $\theta = 30^\circ$, on prend $P$ au dessus de $OA$ alors que pour $\theta = -30^\circ$, on le choisit en dessous de $OA$.On définit alors le cosinus de $\theta$ comme étant l'abscisse du point $P$ et le sinus de $\theta$ comme étant son ordonnée. Pour les représenter, on projette généralement $P$ sur l'axe des abscisses (en notant $C$ sa projection) et sur l'axe des ordonnées (en notant $S$ sa projection), et le cosinus de $\theta$ est donné par $\pm|OC|$ ($+$ si $C$ se situe à droite de $O$ et $-$ sinon) alors que le sinus est égal à $\pm|OS|$ ($+$ si $S$ est au dessus de $O$ et $-$ sinon).
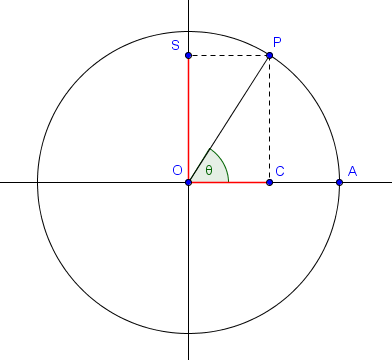
On peut facilement remplir le tableau de valeurs suivantes pour différents angles :
Sinus et cosinus des angles remarquables
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|}
\hline
\theta \ \text{(en degrés)}& 0^\circ & 30^\circ & -30^\circ & 45^\circ & - 45^\circ & 60^\circ & -60^\circ & 90^\circ & -90^\circ \\[1mm]
\hline
\theta \ \text{(en radians)}& 0 & \frac{\pi}{6} & -\frac{\pi}{6} & \frac{\pi}{4} & -\frac{\pi}{4} & \frac{\pi}{3} & -\frac{\pi}{3} & \frac{\pi}{2} & -\frac{\pi}{2} \\[1mm]
\hline
\cos \theta & 1 & \frac{\sqrt{3}}{2} & \frac{\sqrt{3}}{2} & \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} & \frac{1}{2} & \frac{1}{2} & 0 & 0 \\ \\
\hline
\sin \theta & 0 & \frac{1}{2} & -\frac{1}{2} & \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} & 1 & -1 \\ \\
\hline
\end{array}$$
\hline
\theta \ \text{(en degrés)}& 0^\circ & 30^\circ & -30^\circ & 45^\circ & - 45^\circ & 60^\circ & -60^\circ & 90^\circ & -90^\circ \\[1mm]
\hline
\theta \ \text{(en radians)}& 0 & \frac{\pi}{6} & -\frac{\pi}{6} & \frac{\pi}{4} & -\frac{\pi}{4} & \frac{\pi}{3} & -\frac{\pi}{3} & \frac{\pi}{2} & -\frac{\pi}{2} \\[1mm]
\hline
\cos \theta & 1 & \frac{\sqrt{3}}{2} & \frac{\sqrt{3}}{2} & \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} & \frac{1}{2} & \frac{1}{2} & 0 & 0 \\ \\
\hline
\sin \theta & 0 & \frac{1}{2} & -\frac{1}{2} & \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} & 1 & -1 \\ \\
\hline
\end{array}$$
On a aussi plusieurs relations découlant directement de la définition du sinus et du cosinus :
Relations basiques
$$\cos(-\theta) = \cos\theta,$$ $$\sin(-\theta) = -\sin\theta,$$ $$\cos(180^\circ - \theta) = - \cos \theta,$$ $$\sin(180^\circ-\theta) = \sin \theta,$$ $$\cos(90^\circ-\theta) = \sin \theta,$$ $$\sin(90^\circ-\theta) = \cos \theta.$$
Il n'est pas réellement nécessaire de retenir ces formules : on peut facilement les retrouver en examinant le cercle trigonométrique. Ainsi, si on désire exprimer le cosinus de $90^\circ + \theta$ en fonction du sinus ou du cosinus de $\theta$, il suffit de dessiner un angle du type $90^\circ + \theta$ sur le cercle (on le dessine généralement avec $\theta$ assez petit) et de voir s'il est plutôt égal à $\cos \theta$, $- \cos \theta$, $\sin \theta$ ou $- \sin \theta$. Pour notre exemple, on remarquera en fait que $\cos(90^\circ + \theta) = - \sin \theta$.
La relation la plus importante reliant le cosinus et le sinus est en fait la relation bien connue (valable pour tout $\theta$) :
L'identité trigonométrique fondamentale
$$\cos^2\theta + \sin^2 \theta = 1.$$
Il s'agit en fait simplement du théorème de Pythagore dans le triangle $OCP$ plus haut, puisque l'hypothénuse est de longueur $|OP| = 1$ alors que $|OC| = |\cos \theta|$ et $|CP| = |OS| = |\sin \theta|$.
Fonctions tangente et cotangente
Deux autres fonctions du même type que le sinus et le cosinus sont la tangente et la cotangente. On peut également leur donner une signification géométrique sur le cercle trigonométrique. Cette fois, on trace la droite $d$ tangente au cercle en $A$ et la droite $d'$ tangente au cercle en $B$, le point de coordonnées $(0, 1)$. On note alors $T$ l'intersection de $OP$ avec $d$ et $T'$ l'intersection de $OP$ avec $d'$, et la tangente de $\theta$ est donnée par $\pm|AT|$ alors que sa cotangente est donnée par $\pm |BT'|$. A nouveau on choisit le $+$ lorsqu'on est à droite ou au dessus et $-$ sinon.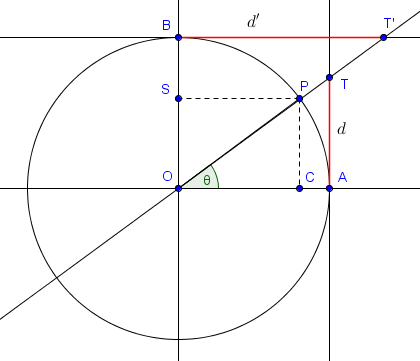
Il faut tout de même remarquer que ces définitions n'ont parfois pas de sens. En effet, lorsque $\theta$ est un multiple de $180^\circ$, la droite $OP$ est parallèle à $d'$ et on ne peut alors pas définir la cotangente de $\theta$. De la même façon, si $\theta$ est du type $90^\circ + k \cdot 180^\circ$ avec $k$ entier, alors la droite $OP$ est parallèle à $d$ et on ne peut pas définir la tangente de $\theta$. On dit que la tangente ou la cotangente de ces angles n'existe pas.
On aurait en fait pu définir la tangente et la cotangente d'un angle sans interprétation géométrique, directement à partir de son sinus et de son cosinus. En effet, les triangles $OAT$ et $OCP$ sont semblables, et on a donc
$$\frac{|AT|}{|OA|} = \frac{|CP|}{|OC|},$$ ce qui devient (il faut discuter les signes mais ceux-ci sont bel et bien corrects) :
$$\tan \theta = \frac{\sin \theta}{\cos \theta}.$$ De la même façon pour les triangles semblables $OBT'$ et $OSP$, on a aussi
$$\mathrm{cotan} \ \theta = \frac{\cos \theta}{\sin \theta}.$$ On a donc la relation
$$\mathrm{cotan} \ \theta = \frac{1}{\tan \theta},$$ ce qui fait qu'on se contente généralement d'étudier la fonction tangente.
On peut, à partir des valeurs des sinus et cosinus des angles remarquables, trouver leur tangente et cotangente :
Tangente et cotangente des angles remarquables
$$\begin{array}{|c|c|c|c|c|c|c|c|c|}
\hline
\theta \ \text{(en degrés)}& 0^\circ & 30^\circ & -30^\circ & 45^\circ & - 45^\circ & 60^\circ & -60^\circ & 90^\circ \\[1mm]
\hline
\theta \ \text{(en radians)}& 0 & \frac{\pi}{6} & -\frac{\pi}{6} & \frac{\pi}{4} & -\frac{\pi}{4} & \frac{\pi}{3} & -\frac{\pi}{3} & \frac{\pi}{2} \\[1mm]
\hline
\tan \theta & 0 & \frac{\sqrt 3}{3} & - \frac{\sqrt 3}{3} & 1 & -1 & \sqrt 3 & - \sqrt 3 & / \\ \\
\hline
\mathrm{cotan} \ \theta & / & \sqrt 3 & - \sqrt 3 & 1 & -1 & \frac{\sqrt 3}{3} & - \frac{\sqrt 3}{3} & 0 \\ \\
\hline
\end{array}$$
\hline
\theta \ \text{(en degrés)}& 0^\circ & 30^\circ & -30^\circ & 45^\circ & - 45^\circ & 60^\circ & -60^\circ & 90^\circ \\[1mm]
\hline
\theta \ \text{(en radians)}& 0 & \frac{\pi}{6} & -\frac{\pi}{6} & \frac{\pi}{4} & -\frac{\pi}{4} & \frac{\pi}{3} & -\frac{\pi}{3} & \frac{\pi}{2} \\[1mm]
\hline
\tan \theta & 0 & \frac{\sqrt 3}{3} & - \frac{\sqrt 3}{3} & 1 & -1 & \sqrt 3 & - \sqrt 3 & / \\ \\
\hline
\mathrm{cotan} \ \theta & / & \sqrt 3 & - \sqrt 3 & 1 & -1 & \frac{\sqrt 3}{3} & - \frac{\sqrt 3}{3} & 0 \\ \\
\hline
\end{array}$$
On a également les formules suivantes, qui peuvent encore une fois être retrouvées facilement à partir du cercle trigonométrique :
Identités trigonométriques
$$\tan(-\theta) = -\tan \theta,$$ $$\mathrm{cotan} (-\theta) = -\mathrm{cotan} \ \theta,$$ $$\tan(180^\circ + \theta) = \tan \theta,$$ $$\mathrm{cotan} (180^\circ + \theta) = \mathrm{cotan}\ \theta,$$ $$\tan(90^\circ-\theta) = \mathrm{cotan} \ \theta,$$ $$\mathrm{cotan} \ (90^\circ-\theta) = \tan \ \theta.$$
Ces formules peuvent enfin également se révéler utiles :
Identités trigonométriques
$$1 + \tan^2 \theta = \frac{1}{\cos^2 \theta},\quad \quad 1 + \mathrm{cotan}^2 \ \theta = \frac{1}{\sin^2 \theta}.$$
Dans un triangle rectangle
Lorsqu'on est en présence d'un triangle rectangle $ABC$, on peut exprimer les différentes fonctions trigonométriques des deux angles aigus à partir des longueurs des côtés du triangle. Ces formules découlent de la définition des fonctions trigonométriques mais n'en sont pas moins primordiales.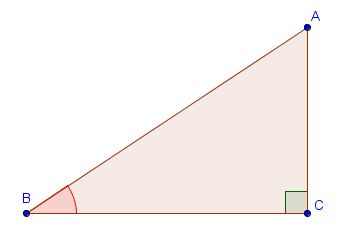
Fonctions trigonométriques dans un triangle rectangle
Dans un triangle $ABC$ rectangle en $C$, on a
$$\sin\widehat{ABC} = \frac{|AC|}{|AB|},$$ $$\cos\widehat{ABC} = \frac{|BC|}{|AB|},$$ $$\tan\widehat{ABC} = \frac{|AC|}{|BC|}.$$
$$\sin\widehat{ABC} = \frac{|AC|}{|AB|},$$ $$\cos\widehat{ABC} = \frac{|BC|}{|AB|},$$ $$\tan\widehat{ABC} = \frac{|AC|}{|BC|}.$$
Un moyen mnémotechnique pour retenir ces formules est l'expression SOHCAHTOA. Il s'agit en effet des initiales de la suite de mots Sinus, Opposé, Hypothénuse - Cosinus, Adjacent, Hypothénuse - Tangente, Opposé, Adjacent.
3. Grandes formules
Formules d'addition et de soustraction
Les fonctions trigonométriques de la somme et de la différence de deux angles se calculent comme suit :Formules d'addition et de soustraction
$$\sin(\alpha+\beta) = \sin \alpha \cos \beta + \sin \beta \cos \alpha,$$ $$\sin(\alpha-\beta) = \sin \alpha \cos \beta - \sin \beta \cos \alpha,$$ $$\cos(\alpha+\beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta,$$ $$\cos(\alpha-\beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta,$$ $$\tan(\alpha+\beta) = \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta},$$ $$\tan(\alpha-\beta) = \frac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta}.$$
Nous n'en donnons pas les démonstrations car elles ne sont pas tout à fait évidentes, d'où l'importance de bien retenir ces formules.
Les formules de duplication suivantes, qui sont des conséquences des formules d'addition, sont elles-aussi très importantes :
Formules de duplication
$$\sin 2\alpha = 2 \sin \alpha \cos \alpha,$$ $$\cos 2\alpha = \cos^2 \alpha - \sin^2 \alpha,$$ $$\tan 2 \alpha = \frac{2\tan \alpha}{1-\tan^2 \alpha}.$$
La deuxième formule peut également se réécrire en utilisant le fait que $\cos^2 \alpha + \sin^2 \alpha = 1$. On a alors
$$\cos 2\alpha = 2 \cos^2 \alpha - 1 = 1 - 2 \sin^2 \alpha.$$
Formules de Carnot
Nous avons vu comment passer d'une formule avec $2 \alpha$ à une formule avec $\alpha$. Parfois, c'est plutôt le contraire que l'on désire faire. Pour cela, on utilise les différentes formules que nous avons vues pour $\cos 2 \alpha$, et on trouve ainsi les formules de Carnot :Formules de Carnot
$$\sin^2 \alpha = \frac{1 - \cos 2 \alpha}{2},$$ $$\cos^2 \alpha = \frac{1 + \cos 2 \alpha}{2}.$$
On peut facilement retrouver celles-ci en connaissant parfaitement la formule pour $\cos 2\alpha$.
Formules en $\tan\left(\frac{\alpha}{2}\right)$
Les formules suivantes permettent, quant à elles, d'exprimer $\sin \alpha$, $\cos \alpha$ et $\tan \alpha$ uniquement en fonction de $\displaystyle\tan\left(\frac{\alpha}{2}\right)$. Si on se retrouve à devoir résoudre une équation impliquant plusieurs fonctions trigonométriques d'un même angle, on peut par exemple utiliser ces formules pour obtenir une équation ne faisant plus intervenir que la tangente de la moitié de l'angle. On peut alors remplacer cette tangente par une inconnue $x$ et résoudre l'équation pour $x$ (cela consistant souvent à trouver les racines d'un polynôme). Le degré du polynôme devient cependant vite élevé, ce qui empêche souvent une telle résolution (à moins qu'il n'ait des racines évidentes).Formules en $\tan\left(\frac{\alpha}{2}\right)$
$$\sin \alpha = \frac{2 \tan \left(\frac{\alpha}{2}\right)}{1 + \tan^2\left(\frac{\alpha}{2}\right)},$$ $$\cos \alpha = \frac{1 - \tan^2 \left(\frac{\alpha}{2}\right)}{1 + \tan^2\left(\frac{\alpha}{2}\right)},$$ $$\tan \alpha = \frac{2 \tan \left(\frac{\alpha}{2}\right)}{1 - \tan^2\left(\frac{\alpha}{2}\right)}.$$
Formules de Simpson
Les formules de Simpson permettent de transformer une somme de deux fonctions trigonométriques en un produit. Cela se révèle utile si, par exemple, on doit résoudre une équation du type $\sin \alpha + \sin 5\alpha = 0$. On peut en effet dans un tel cas transformer la somme en un produit, ce qui simplifie largement la résolution de l'équation.Formules de Simpson
$$\sin \alpha + \sin \beta = 2 \sin \left(\frac{\alpha+\beta}{2}\right) \cos \left(\frac{\alpha-\beta}{2}\right),$$ $$\sin \alpha - \sin \beta = 2 \cos \left(\frac{\alpha+\beta}{2}\right) \sin \left(\frac{\alpha-\beta}{2}\right),$$ $$\cos \alpha + \cos \beta = 2 \cos \left(\frac{\alpha+\beta}{2}\right) \cos \left(\frac{\alpha-\beta}{2}\right),$$ $$\cos \alpha - \cos \beta = - 2 \sin \left(\frac{\alpha+\beta}{2}\right) \sin \left(\frac{\alpha-\beta}{2}\right).$$
Ces formules se démontrent simplement en combinant deux formules d'addition ou de soustraction. Il suffit en effet d'écrire
$$\alpha = \left(\frac{\alpha+\beta}{2}\right) + \left(\frac{\alpha-\beta}{2}\right) \quad \text{ et } \quad \beta = \left(\frac{\alpha+\beta}{2}\right) - \left(\frac{\alpha-\beta}{2}\right)$$ et d'ainsi calculer $\sin \alpha$ ou $\cos \alpha$ comme un (co)sinus d'une somme ainsi que $\sin \beta$ ou $\cos \beta$. Les termes obtenus additionnés se simplifient pour donner les formules de Simpson.
4. Fonctions réciproques
Parfois, au lieu de calculer le sinus ou le cosinus d'un angle, on aimerait faire le calcul inverse. On peut en effet être en présence d'un angle dont on ne connait pas l'amplitude mais dont on est parvenu à calculer le sinus (par exemple à partir de la longueur des côtés d'un triangle rectangle). C'est l'intérêt des fonctions trigonométriques inverses : elles associent à un nombre réel l'amplitude d'un angle dont le nombre est le sinus (ou le cosinus ou la tangente).
Le lecteur n'est cependant pas sans savoir qu'il existe plusieurs angles différents ayant le même sinus (ou cosinus ou tangente). Les fonctions trigonométriques inverses devront donc "faire un choix" parmi tous les angles pouvant convenir. Pour chacune, on choisira en fait l'amplitude de l'angle le plus petit possible en valeur absolue. C'est de cette façon que l'on définit les fonctions arc sinus, arc cosinus et arc tangente, inverses du sinus, du cosinus et de la tangente respectivement.
Le lecteur n'est cependant pas sans savoir qu'il existe plusieurs angles différents ayant le même sinus (ou cosinus ou tangente). Les fonctions trigonométriques inverses devront donc "faire un choix" parmi tous les angles pouvant convenir. Pour chacune, on choisira en fait l'amplitude de l'angle le plus petit possible en valeur absolue. C'est de cette façon que l'on définit les fonctions arc sinus, arc cosinus et arc tangente, inverses du sinus, du cosinus et de la tangente respectivement.
- La fonction $\displaystyle\arcsin : [-1, 1] \to \left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$ envoie un réel $x$ compris entre $-1$ et $1$ (inclus) sur l'amplitude mesurée en radian d'un angle dont le sinus vaut $x$. Il existe plusieurs telles amplitudes, mais elle renvoie en fait toujours l'amplitude dans l'intervalle $\displaystyle\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$.
- La fonction $\displaystyle\arccos : [-1, 1] \to \left[0, \pi\right]$ envoie un réel $x$ compris entre $-1$ et $1$ (inclus) sur l'amplitude mesurée en radian d'un angle dont le cosinus vaut $x$. Cette fois-ci, la fonction arc cosinus renvoie l'amplitude dans l'intervalle $\displaystyle\left[0, \pi\right]$ qui convient.
- La fonction $\displaystyle\arctan : \mathbb{R} \to \left]-\frac{\pi}{2}, \frac{\pi}{2}\right[$ envoie un réel $x$ sur l'amplitude mesurée en radian d'un angle dont la tangente vaut $x$. Le codomaine de la fonction arc tangente est dans ce cas $\displaystyle\left]-\frac{\pi}{2}, \frac{\pi}{2}\right[$.