Théorie > Inégalités > Boîte à outils des inégalités
Prérequis
Résumé
Ce chapitre rassemble différentes astuces courantes et changements de variables particuliers permettant parfois de simplifier des inégalités. En particulier, il existe plusieurs méthodes pour faire disparaître une condition a priori difficile à exploiter du type $abc=1$.
Ce chapitre a été écrit par B. Legat et N. Radu et mis en ligne le 8 décembre 2014.
1. Changements de variables classiques
Voici quelques changements de variables classiques qui peuvent se révéler utiles dans différentes situations. Il s'agit là de différentes possibilités mais elles ne fonctionnent bien sûr pas à tous les coups. Nous présentons simplement différentes méthodes qui sont connues pour parfois simplifier des inégalités.
- Si on a deux variables $a, b \in \mathbb{R}$, on peut toujours poser
$$\left\{\begin{align}
a &= \alpha + \beta\\
b &= \alpha - \beta
\end{align}\right.$$ avec $\alpha, \beta \in \mathbb{R}$. Il suffit en effet de prendre
$$\left\{\begin{align}
\alpha &= \frac{a+b}{2}\\[2mm]
\beta &= \frac{a-b}{2}
\end{align}\right.$$ Ce changement de variables permet parfois de se ramener à une inégalité plus simple ou plus parlante. - Si on a trois variables $a,b,c \in \mathbb{R}$ sous la contrainte $a+b+c = 0$, on peut être tenté de remplacer $c$ par $-a-b$ dans l'inégalité à prouver. Malheureusement, cela brise alors la symétrie éventuelle de l'inégalité ce qui la complique inévitablement. Une meilleure idée pour se débarrasser de la contrainte $a+b+c = 0$ est de poser
$$\left\{\begin{align}
a &= \beta - \gamma\\
b &= \gamma - \alpha\\
c &= \alpha - \beta
\end{align}\right.$$ pour des $\alpha, \beta, \gamma \in \mathbb{R}$. On peut en fait même donner une valeur particulière à l'une des trois nouvelles variables (par exemple prendre $\alpha = 0$) mais cela brisera à nouveau la symétrie de l'inégalité que nous cherchons pourtant à préserver. Ce changement de variable est très utile puisqu'il permet de se débarrasser de la contrainte tout en préservant une certaine harmonie.
Remarque : Ce changement de variable peut évidemment être également effectué avec $n$ variables $a_1, \ldots, a_n$ vérifiant $a_1+\ldots+a_n = 0$. On pose dans ce cas
$$\left\{\begin{align}
a_1 &= \alpha_1 - \alpha_2 \\
a_2 &= \alpha_2 - \alpha_3 \\
& \vdots \\
a_n &= \alpha_n - \alpha_1
\end{align}\right.$$ - Si on a trois variables $a,b,c \in \mathbb{R}$ sous la contrainte $abc = 1$, alors le même problème que dans le point précédent se pose : on peut remplacer $c$ par $\frac{1}{ab}$ mais cela complique généralement l'inégalité. On préfère donc effectuer le changement de variables
$$\left\{\begin{align}
a & = \frac{\alpha}{\beta} \\[1mm]
b &= \frac{\beta}{\gamma} \\[1mm]
c &= \frac{\gamma}{\alpha}
\end{align}\right.$$
Remarque : A nouveau, si on a $n$ variables $a_1, \ldots, a_n$ vérifiant $a_1 a_2 \ldots a_n = 1$, alors on peut aussi appliquer le même type de changement de variables. - On peut aussi passer d'une contrainte de type $a+b+c = 0$ à une contrainte de type $\alpha\beta\gamma = 1$ en posant
$$\left\{\begin{align}
a &= \ln \alpha \\
b &= \ln \beta \\
c &= \ln \gamma
\end{align}\right.$$ avec $\alpha, \beta, \gamma \in \mathbb{R}_0^+$. Dans le sens contraire, on peut bien sûr poser
$$\left\{\begin{align}
\alpha &= e^a \\
\beta &= e^b \\
\gamma &= e^c
\end{align}\right.$$ - Si on est en présence d'une contrainte du type $a+b+c = 1$ plutôt que $a+b+c = 0$, on peut tout de même être tenté d'utiliser la transformation expliquée au point 2. Cela peut effectivement être fait en posant au préalable $a = \frac 13 + a'$, $b = \frac 13 + b'$, $c = \frac 13 + c'$ de sorte que $a'+b'+c'=0$.
- Si on a une suite croissante $a_0 \leq a_1 \leq a_2 \leq \ldots \leq a_n$, on peut poser la suite de réels positifs $b_1, \ldots, b_n$ tels que $b_k = a_k - a_{k-1}$. S'il est mentionné que les $a_k$ sont positifs (c'est à dire que $a_0$ est positif) ou qu'on montre que l'inégalité est vérifiée dans le cas contraire, on peut poser $b_0 = a_0$ qui est alors positif également.
2. Inégalités homogènes
Une inégalité est dite homogène si, lorsqu'on multiplie chaque variable par une même constante, on retombe sur la même inégalité.
Le plus simple pour comprendre ce dont il s'agit est d'observer un exemple.
Exemple : L'inégalité
$$\frac{a(b+c)}{bc} + \frac{b(a+c)}{ac} + \frac{c(a+b)}{ab} \geq 6$$ est homogène. En effet, si l'on multiplie chacune des variables $a$, $b$ et $c$ par une constante $k$, alors l'inégalité devient
$$\frac{ka(kb+kc)}{k^2bc} + \frac{kb(ka+kc)}{k^2ac} + \frac{kc(ka+kb)}{k^2ab} \geq 6$$ et tous les $k$ se simplifient, ce qui nous ramène à l'inégalité de départ.
Remarque importante : Lorsqu'on est en présence d'une inégalité homogène, on peut donc supposer que la somme ou le produit des variables vaut $1$. On ne peut cependant pas effectuer ces deux suppositions en même temps ! Une fois que l'on suppose que la somme des variables vaut $1$, l'homogénéité a été exploitée et il n'est plus question de rajouter la supposition supplémentaire que le produit des variables vaut $1$. On peut donc juste tenter d'utiliser une de ces deux simplifications à la fois.
Supposer que la somme ou le produit vaut $1$ est ce qui se fait assez couramment, mais il n'est bien sûr pas interdit de faire une supposition plus farfelue qui conviendrait mieux au problème auquel on est confronté. On peut donc par exemple plutôt supposer que $a_1 a_2^2 \ldots a_n^n = 1$ si cela semble mieux convenir (mais il faut être certain que le raisonnement expliqué dans cette section fonctionne à nouveau).
Autre remarque importante : Si les variables ne sont pas supposées positives, alors il faut faire attention à ne pas utiliser l'astuce ci-dessus aveuglément. Par exemple, si on considère l'inégalité
$$x^3 + y^3 + z^3 \geq 3xyz,$$ et que l'on souhaite utiliser l'homogénéité pour supposer que $xyz = 1$, il faut rester sur ses gardes si $x, y, z$ ne sont pas supposés positifs. En effet, si on remplace $x$, $y$ et $z$ par $kx$, $ky$ et $kz$ et qu'on divise l'inégalité par $k^3$ pour le faire disparaître, alors l'inégalité doit changer de sens lorsque $k$ est négatif ! Il est difficile de donner une règle générale dans ce genre de situation, mais le conseil est le suivant : quand les variables ne sont pas supposées positives, refaites le raisonnement ci-dessus avec la simplification par $k$ pour être sûr de pouvoir utiliser l'homogénéité sans risque.
Le plus simple pour comprendre ce dont il s'agit est d'observer un exemple.
Exemple : L'inégalité
$$\frac{a(b+c)}{bc} + \frac{b(a+c)}{ac} + \frac{c(a+b)}{ab} \geq 6$$ est homogène. En effet, si l'on multiplie chacune des variables $a$, $b$ et $c$ par une constante $k$, alors l'inégalité devient
$$\frac{ka(kb+kc)}{k^2bc} + \frac{kb(ka+kc)}{k^2ac} + \frac{kc(ka+kb)}{k^2ab} \geq 6$$ et tous les $k$ se simplifient, ce qui nous ramène à l'inégalité de départ.
Astuce de résolution
Le fait qu'une inégalité soit homogène peut sembler peu utile (puisqu'un changement de variables semble ne pas modifier l'inégalité), mais il s'agit en fait d'une propriété très intéressante. En effet, lorsqu'on est en présence d'une inégalité homogène de variables $a_1, \ldots, a_n$, on peut supposer sans perte de généralité que les variables en question vérifient une propriété supplémentaire :- On peut supposer que $a_1 + \ldots + a_n = 1$ :
En général, si on parvient à montrer une inégalité quelconque uniquement pour les variables $a_i$ dont la somme vaut $1$, on n'a pas encore achevé la preuve de l'inégalité. En effet, celle-ci n'est peut-être pas vraie pour certaines variables $a_i$ dont la somme est différente de $1$. Cela dit, lorsque l'inégalité est homogène, on ne perd en fait aucune généralité en supposant que la somme des variables vaut $1$ :
Imaginons que nous ayions montré une certaine inégalité homogène en supposant au préalable que $a_1+\ldots+a_n = 1$. Nous affirmons que l'inégalité est alors également vraie même si $a_1+\ldots+a_n = k \neq 1$. En effet, dans ce cas, on peut effectuer le changement de variable $\displaystyle a'_i = \frac{a_i}{k}$ pour tout $i \in \{1, \ldots, n\}$. Par homogénéité, l'inégalité avec les $a_i$ est alors équivalente à la même inégalité avec les $a'_i$, mais la somme de ces derniers vaut désormais $1$ et nous nous sommes ainsi ramenés au cas que nous avions déjà traité.
Remarque : Il faut tout de même faire attention au cas où $k = 0$. En effet, si les conditions de l'énoncé sur les variables $a_i$ n'empêchent pas la somme $a_1+\ldots + a_n$ de valoir $0$, alors il faut traiter ce cas à part. Dans la pratique, cela arrive cependant rarement puisqu'on suppose souvent que les variables $a_i$ sont (strictement) positives. - On peut supposer que $a_1a_2\ldots a_n = 1$ :
Il s'agit là de la même astuce. Si on a démontré une inégalité homogène sous la condition supplémentaire que $a_1a_2\ldots a_n = 1$, alors elle est également vraie lorsque $a_1a_2\ldots a_n = k \neq 1$. On peut en effet dans ce cas effectuer le changement de variables $\displaystyle a'_i = \frac{a_i}{\sqrt[n]{k}}$ qui nous ramène au cas déjà traité.
Remarque : Là aussi, il faut traiter à part le cas où l'un des $a_i$ est nul puisque cela impliquerait $a_1a_2\ldots a_n = 0$ et on ne peut pas appliquer le raisonnement précédent dans ce cas.
Remarque importante : Lorsqu'on est en présence d'une inégalité homogène, on peut donc supposer que la somme ou le produit des variables vaut $1$. On ne peut cependant pas effectuer ces deux suppositions en même temps ! Une fois que l'on suppose que la somme des variables vaut $1$, l'homogénéité a été exploitée et il n'est plus question de rajouter la supposition supplémentaire que le produit des variables vaut $1$. On peut donc juste tenter d'utiliser une de ces deux simplifications à la fois.
Supposer que la somme ou le produit vaut $1$ est ce qui se fait assez couramment, mais il n'est bien sûr pas interdit de faire une supposition plus farfelue qui conviendrait mieux au problème auquel on est confronté. On peut donc par exemple plutôt supposer que $a_1 a_2^2 \ldots a_n^n = 1$ si cela semble mieux convenir (mais il faut être certain que le raisonnement expliqué dans cette section fonctionne à nouveau).
Autre remarque importante : Si les variables ne sont pas supposées positives, alors il faut faire attention à ne pas utiliser l'astuce ci-dessus aveuglément. Par exemple, si on considère l'inégalité
$$x^3 + y^3 + z^3 \geq 3xyz,$$ et que l'on souhaite utiliser l'homogénéité pour supposer que $xyz = 1$, il faut rester sur ses gardes si $x, y, z$ ne sont pas supposés positifs. En effet, si on remplace $x$, $y$ et $z$ par $kx$, $ky$ et $kz$ et qu'on divise l'inégalité par $k^3$ pour le faire disparaître, alors l'inégalité doit changer de sens lorsque $k$ est négatif ! Il est difficile de donner une règle générale dans ce genre de situation, mais le conseil est le suivant : quand les variables ne sont pas supposées positives, refaites le raisonnement ci-dessus avec la simplification par $k$ pour être sûr de pouvoir utiliser l'homogénéité sans risque.
3. Inégalités symétriques
Une inégalité est dite symétrique si, lorsqu'on permute les variables de manière quelconque, on retombe sur la même inégalité. Cela revient à dire que chaque variable joue le même rôle dans l'inégalité et qu'aucune n'est "privilégiée".
Encore une fois, le mieux est d'observer des exemples.
Exemple : L'inégalité
$$\frac{a(b+c)}{bc} + \frac{b(a+c)}{ac} + \frac{c(a+b)}{ab} \geq 6,$$ en plus d'être homogène comme nous l'avons vu, est symétrique. En effet, si l'on permute les variables $a$, $b$ et $c$, on retombe chaque fois sur la même inégalité. Par exemple, en remplaçant $a$ par $b$, $b$ par $c$ et $c$ par $a$, on obtient
$$\frac{b(c+a)}{ca} + \frac{c(b+a)}{ba} + \frac{a(b+c)}{bc} \geq 6$$ qui est exactement la même inégalité.
Contre-exemple : L'inégalité
$$\frac{a^2+b^2}{ab} + \frac{b^2+c^2}{bc} + \frac{c^2+d^2}{cd} + \frac{d^2+a^2}{da} \geq 8$$ n'est pas symétrique. En effet, si on interchange simplement les variables $a$ et $b$, on tombe sur l'inégalité
$$\frac{b^2+a^2}{ba} + \frac{a^2+c^2}{ac} + \frac{c^2+d^2}{cd} + \frac{d^2+b^2}{db} \geq 8$$ qui n'est visiblement pas la même que l'inégalité initiale.
Encore une fois, le mieux est d'observer des exemples.
Exemple : L'inégalité
$$\frac{a(b+c)}{bc} + \frac{b(a+c)}{ac} + \frac{c(a+b)}{ab} \geq 6,$$ en plus d'être homogène comme nous l'avons vu, est symétrique. En effet, si l'on permute les variables $a$, $b$ et $c$, on retombe chaque fois sur la même inégalité. Par exemple, en remplaçant $a$ par $b$, $b$ par $c$ et $c$ par $a$, on obtient
$$\frac{b(c+a)}{ca} + \frac{c(b+a)}{ba} + \frac{a(b+c)}{bc} \geq 6$$ qui est exactement la même inégalité.
Contre-exemple : L'inégalité
$$\frac{a^2+b^2}{ab} + \frac{b^2+c^2}{bc} + \frac{c^2+d^2}{cd} + \frac{d^2+a^2}{da} \geq 8$$ n'est pas symétrique. En effet, si on interchange simplement les variables $a$ et $b$, on tombe sur l'inégalité
$$\frac{b^2+a^2}{ba} + \frac{a^2+c^2}{ac} + \frac{c^2+d^2}{cd} + \frac{d^2+b^2}{db} \geq 8$$ qui n'est visiblement pas la même que l'inégalité initiale.
Astuce de résolution
Lorsqu'on est en présence d'une inégalité symétrique, on peut si on le désire supposer sans perte de généralité que les variables sont dans un certain ordre. En effet, vu qu'une permutation des variables ne change en rien l'inégalité, on peut toujours les permuter de sorte qu'elles soient, par exemple, en ordre croissant. Si les variables sont $a_1, \ldots, a_n$, on peut donc supposer que $a_1 \leq a_2 \leq \ldots \leq a_n$. Cela peut bien sûr se révéler utile dans la résolution d'une inégalité.4. Transformation de Ravi
La transformation de Ravi est à nouveau un changement de variables pouvant être effectué sous certaines conditions.
Celle-ci peut en fait être appliquée lorsque l'on est en présence de trois variables $a$, $b$ et $c$ positives dont on sait qu'elles correspondent aux longueurs des trois côtés d'un même triangle, c'est-à-dire qu'elles vérifient les inégalités
$$\begin{align}
a + b & \geq c,\\[1mm]
b + c & \geq a,\\[1mm]
c + a & \geq b.
\end{align}$$ En pratique, cette condition est généralement énoncée telle quelle dans l'énoncé du problème : celui-ci commence par exemple par "Montrer que si $a$, $b$ et $c$ sont les longueurs des côtés d'un triangle, alors ils vérifient l'inégalité suivante".
La transformation de Ravi consiste alors à remplacer $a$, $b$ et $c$ par $x$, $y$ et $z$ (positifs) en effectuant le changement de variable
$$\left\{\begin{align}
a & = y+z \\[1mm]
b &= z + x \\[1mm]
c &= x + y
\end{align}\right.$$ ce qui revient en fait à poser
$$\left\{\begin{align}
x & = \frac{b + c - a}{2} \\[2mm]
y & = \frac{c + a - b}{2} \\[2mm]
z & = \frac{a + b - c}{2}
\end{align}\right.$$
Il existe une façon géométrique de visualiser ce changement de variables. En effet, si on dessine le triangle dont les longueurs des côtés sont $a$, $b$ et $c$, alors les valeurs de $x$, $y$ et $z$ peuvent être trouvées en traçant le cercle inscrit au triangle et évaluant les distances des points de tangence aux différents sommets, comme illustré sur la figure suivante.
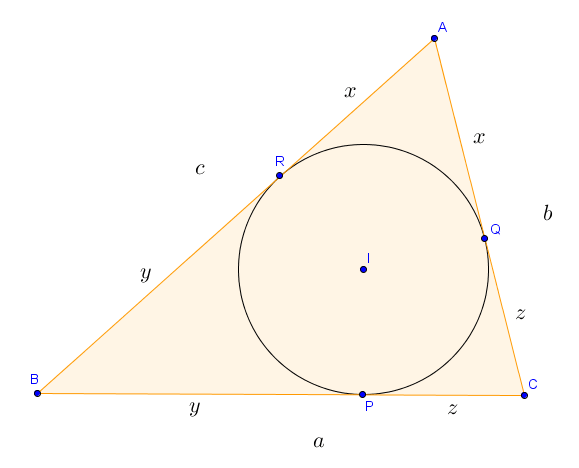
Sur cette figure, on a $a = |BC|$, $b = |AC|$ et $c = |AB|$. De plus, on a les égalités de longueurs $|AQ| = |AR| = x$, $|BP| = |BR| = y$ et $|CP| = |CQ| = z$ car les triangles $AQI$ et $ARI$ sont isométriques, tout comme les triangles $BPI$ et $BRI$ et les triangles $CPI$ et $CQI$.
Cette transformation est d'une grande utilité lorsque les variables $a$, $b$ et $c$ sont supposées être les longueurs d'un triangle. En effet, elle permet de passer à une inégalité en $a$, $b$ et $c$ sous cette contrainte (qu'il ne semble a priori pas évident d'utiliser) à une inégalité équivalente en $x$, $y$ et $z$ sans contrainte. En effet, il n'y a plus aucune contrainte sur $x$, $y$ et $z$ (mis à part qu'ils sont positifs) puisque tout triplet de réels positifs $(x,y,z)$ donne exactement un triplet $(a,b,c)$ de réels vérifiant les inégalités triangulaires.
Cela est moins courant, mais il est aussi possible d'utiliser cette transformation même lorsque $a$, $b$ et $c$ sont des réels positifs quelconques. En effet, on peut alors séparer le problème en deux cas : l'un où l'une des $3$ inégalités triangulaires n'est pas vérifiée (ce qui peut permettre de progresser dans le problème) et l'autre où on peut utiliser la transformation de Ravi.
La difficulté dans ces cas là est de penser à l'utiliser. L'astuce c'est de repérer les expressions $b+c-a, a+b-c, c+a-b$. En effet la positivité de ces expressions est équivalente au fait que $a,b,c$ sont les côtés d'un triangle donc voir ces expressions apparaitre est un signe qu'une transformation de Ravi peut simplifier les choses.
$$S = \sqrt{p(p-a)(p-b)(p-c)}$$ où $p = \frac{a+b+c}{2}$ est le demi périmètre du triangle. Après la transformation de Ravi, cette formule devient
$$S = \sqrt{(x+y+z)xyz}.$$
Celle-ci peut en fait être appliquée lorsque l'on est en présence de trois variables $a$, $b$ et $c$ positives dont on sait qu'elles correspondent aux longueurs des trois côtés d'un même triangle, c'est-à-dire qu'elles vérifient les inégalités
$$\begin{align}
a + b & \geq c,\\[1mm]
b + c & \geq a,\\[1mm]
c + a & \geq b.
\end{align}$$ En pratique, cette condition est généralement énoncée telle quelle dans l'énoncé du problème : celui-ci commence par exemple par "Montrer que si $a$, $b$ et $c$ sont les longueurs des côtés d'un triangle, alors ils vérifient l'inégalité suivante".
La transformation de Ravi consiste alors à remplacer $a$, $b$ et $c$ par $x$, $y$ et $z$ (positifs) en effectuant le changement de variable
$$\left\{\begin{align}
a & = y+z \\[1mm]
b &= z + x \\[1mm]
c &= x + y
\end{align}\right.$$ ce qui revient en fait à poser
$$\left\{\begin{align}
x & = \frac{b + c - a}{2} \\[2mm]
y & = \frac{c + a - b}{2} \\[2mm]
z & = \frac{a + b - c}{2}
\end{align}\right.$$
Il existe une façon géométrique de visualiser ce changement de variables. En effet, si on dessine le triangle dont les longueurs des côtés sont $a$, $b$ et $c$, alors les valeurs de $x$, $y$ et $z$ peuvent être trouvées en traçant le cercle inscrit au triangle et évaluant les distances des points de tangence aux différents sommets, comme illustré sur la figure suivante.

Sur cette figure, on a $a = |BC|$, $b = |AC|$ et $c = |AB|$. De plus, on a les égalités de longueurs $|AQ| = |AR| = x$, $|BP| = |BR| = y$ et $|CP| = |CQ| = z$ car les triangles $AQI$ et $ARI$ sont isométriques, tout comme les triangles $BPI$ et $BRI$ et les triangles $CPI$ et $CQI$.
Cette transformation est d'une grande utilité lorsque les variables $a$, $b$ et $c$ sont supposées être les longueurs d'un triangle. En effet, elle permet de passer à une inégalité en $a$, $b$ et $c$ sous cette contrainte (qu'il ne semble a priori pas évident d'utiliser) à une inégalité équivalente en $x$, $y$ et $z$ sans contrainte. En effet, il n'y a plus aucune contrainte sur $x$, $y$ et $z$ (mis à part qu'ils sont positifs) puisque tout triplet de réels positifs $(x,y,z)$ donne exactement un triplet $(a,b,c)$ de réels vérifiant les inégalités triangulaires.
Cela est moins courant, mais il est aussi possible d'utiliser cette transformation même lorsque $a$, $b$ et $c$ sont des réels positifs quelconques. En effet, on peut alors séparer le problème en deux cas : l'un où l'une des $3$ inégalités triangulaires n'est pas vérifiée (ce qui peut permettre de progresser dans le problème) et l'autre où on peut utiliser la transformation de Ravi.
La difficulté dans ces cas là est de penser à l'utiliser. L'astuce c'est de repérer les expressions $b+c-a, a+b-c, c+a-b$. En effet la positivité de ces expressions est équivalente au fait que $a,b,c$ sont les côtés d'un triangle donc voir ces expressions apparaitre est un signe qu'une transformation de Ravi peut simplifier les choses.
Formule de Héron
La transformation de Ravi se combine bien avec la formule de Héron, expliquée en géométrie. Celle-ci stipule que l'aire d'un triangle de côtés $a$, $b$ et $c$ vaut$$S = \sqrt{p(p-a)(p-b)(p-c)}$$ où $p = \frac{a+b+c}{2}$ est le demi périmètre du triangle. Après la transformation de Ravi, cette formule devient
$$S = \sqrt{(x+y+z)xyz}.$$