Théorie > Combinatoire > Double comptage

Ce chapitre présente la méthode du double comptage, qui permet de démontrer des résultats théoriques comme la formule de Cayley mais qui se révèle surtout être un outil très puissant pour démontrer des problèmes de combinatoire de haut niveau.

Le double comptage, aussi appelé double dénombrement, est une technique qui consiste à calculer une quantité combinatoire de deux manières différentes. Cette méthode permet de prouver des formules combinatoires, mais aussi de résoudre des problèmes d'olympiades a priori très difficiles.

Pour illustrer cette technique, nous allons d'abord examiner un exemple assez simple. Considérons le problème suivant, déjà rencontré précédemment :


Il y a deux façons de résoudre ce problème :

1. Pour construire un sous-ensemble $E \subseteq \{1, 2, \ldots, n\}$, on peut simplement décider pour chaque élément $i$ entre $1$ et $n$ si on le met dans $E$ ou non. On a donc deux choix pour l'élément $1$, deux choix pour $2$, ... et deux choix pour $n$. On a donc au total $2^n$ sous-ensembles.


2. On peut décider de d'abord compter les sous-ensembles de $\{1, 2, \ldots, n\}$ ayant $0$ élément, puis ceux ayant $1$ élément, ... jusque ceux ayant $n$ éléments. Pour construire un sous-ensemble $E \subseteq \{1, 2, \ldots, n\}$ ayant exactement $k$ éléments, on doit simplement choisir ces $k$ éléments et on a dès lors $C^k_n$ tels sous-ensembles. Au total, on a donc $C^0_n + C^1_n + \ldots + C^{n-1}_n + C^n_n$ sous-ensembles.

Nous avons résolu le problème de deux manières et trouvé deux expressions différentes. Puisque nos deux manières de procéder sont correctes, on en déduit que les deux expressions obtenues sont identiques, et nous venons dès lors de prouver la formule
$$C^0_n + C^1_n + \ldots + C^{n-1}_n + C^n_n = 2^n,$$ que nous avions déjà prouvée à l'aide de la formule de Newton.

La technique du double comptage permet par exemple de prouver la formule de Cayley.

Pour expliquer ce à quoi cette formule s'intéresse, nous devons d'abord définir la notion d'arbre. Par définition, un arbre est un graphe (non-orienté) connexe qui ne contient aucun cycle. Un exemple d'arbre est donné ci-dessous.


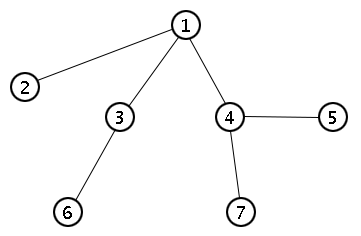
Une propriété fondamentale d'un arbre est que son nombre d'arêtes est exactement égal à son nombre de sommets moins un. L'idée est que, si l'on est en présence de $n$ sommets, alors il faut au minimum $n-1$ arêtes pour être connexe; mais si on prend plus de $n-1$ arêtes, alors on créera un cycle. Pour avoir un arbre, il faut donc exactement $n-1$ arêtes. Une autre façon de le justifier est d'utiliser la formule d'Euler $s-a+f = 2$. En effet, comme un arbre ne possède pas de cycle, des arêtes ne délimitent jamais aucune zone du plan et le nombre de faces $f$ est donc toujours égal à $1$. On en déduit que $a = s-1$.

Maintenant que la notion d'arbre a été expliquée, nous pouvons nous demander, étant donné $n$ sommets, combien d'arbres distincts il est possible de créer à partir de ces $n$ sommets. On sait qu'il faut relier ces sommets avec $n-1$ arêtes, mais il y a bien sûr plusieurs manières de placer ces arêtes. La formule de Cayley est la réponse à cette question, que nous reformulons ci-dessous.


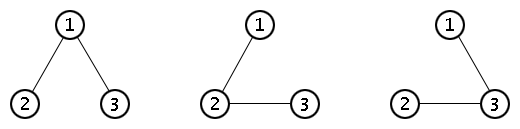
On voit directement que $T_2 = 1$ et $T_3 = 3$ (voir schémas suivants), mais c'est déjà plus fastidieux de calculer $T_4$.


Il ne semble pas évident de trouver une formule pour $T_n$ en utilisant les méthodes classiques présentées. En effet, on peut par exemple essayer de placer les arêtes une par une et de compter le nombre de possibilités à chaque placement, mais ce nombre dépendra toujours des choix faits précédemment, ce qui rend le calcul impossible.

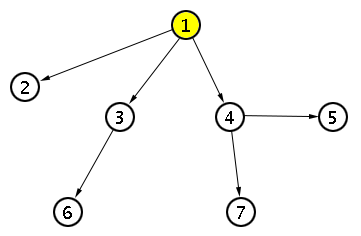
Une façon de calculer $T_n$ (il existe d'autres manières de le faire mais elles sont réputées moins élégantes) est d'utiliser le double comptage. La quantité que nous allons évaluer à deux reprises est le nombre de façons d'ajouter $n-1$ arêtes orientées (l'ordre des ajouts ayant de l'importance) à $n$ sommets initialement disjoints pour obtenir un arbre enraciné orienté. Par définition, un arbre enraciné orienté est un arbre où un sommet est privilégié (on l'appelle la racine de l'arbre) et où les arêtes sont toutes orientées dans la direction opposée à la racine. Un exemple d'arbre enraciné orienté est donné sur la figure suivante : la racine est le sommet numéroté $1$.


Nous pouvons calculer cette quantité de deux façons différentes :

1. Pour la première méthode, on suppose connaître la valeur de $T_n$. On connaît donc le nombre d'arbres (non enracinés et non orientés) qu'on peut construire sur $n$ sommets. Pour chacun de ces $T_n$ arbres, il y a $n$ choix possibles de racines. Le choix de la racine détermine par ailleurs directement l'orientation que les arêtes de l'arbre doivent avoir. On a donc exactement $n \cdot T_n$ arbres enracinés orientés, et il reste à voir pour chacun le nombre de façons d'ajouter les $n-1$ arêtes une par une pour obtenir l'arbre. Clairement, cela revient simplement à choisir l'ordre dans lequel on ajoute les arêtes, et il y a $(n-1)!$ tels ordres. Au total, on en déduit que le nombre de façons d'ajouter $n-1$ arêtes orientées à $n$ sommets pour obtenir un arbre enraciné orienté est égal à
   $$n \cdot T_n \cdot (n-1)! = n! \cdot T_n.$$


2. Pour la deuxième méthode, on adopte une approche classique : on va ajouter les arêtes une par une et voir, à chaque étape, combien il y a de choix possibles. Au départ, il y a $n$ sommets disjoints, qu'on peut voir comme étant $n$ arbres enracinés orientés triviaux (chaque arbre est constitué d'un seul sommet : sa racine). À chaque fois que l'on va ajouter une arête à notre graphe, on va relier deux arbres enracinés orientés existants pour qu'ils ne forment qu'un seul arbre enraciné orienté. Pour ce faire, il faut que l'arête que l'on ajoute aille d'un sommet quelconque de l'un des arbres à la racine d'un autre arbre. De cette façon, après la $k$-ème arête on sera en présence de $n-k$ arbres enracinés orientés. À la fin du processus, on aura donc $n-(n-1) = 1$ arbre enraciné orienté comme voulu. Il faut noter que cette façon de procéder (ajouter à chaque fois une arête d'un sommet quelconque d'un arbre vers la racine d'un autre arbre) est la seule manière qui permette d'obtenir un arbre enraciné orienté valide à la fin. En effet, si on ajoutait une autre arête, alors on aurait soit plus un arbre soit une orientation contradictoire.
   Il reste maintenant à évaluer le nombre de façons de suivre ce processus. Si $k-1$ arêtes ont déjà été placées, on est en présence de $n-k+1$ arbres et on désire rajouter la $k$-ème arête. Nous avons $n$ choix pour l'origine de cette arête comme on peut choisir n'importe quel sommet. Par contre, le point d'arrivée de cette arête doit être une racine d'un arbre autre que l'arbre contenant le point d'origine choisi : il y a donc $n-k$ choix pour celle-ci. Au total, on a donc $n\cdot(n-k)$ choix à la $k$-ème étape, d'où on obtient
   $$(n\cdot(n-1)) \cdot (n\cdot(n-2)) \cdot \ldots \cdot (n \cdot 2) \cdot (n \cdot 1) = n^{n-1} \cdot (n-1)! = n^{n-2} \cdot n!.$$

Nous avons donc prouvé que $n! \cdot T_n = n^{n-2}\cdot n!$, ce qui signifie que l'on a la formule suivante pour $T_n$.


Cette formule est intéressante en tant que telle, mais c'est surtout la méthode utilisée pour la prouver qui est digne d'intérêt.

Certains problèmes de combinatoire, qui paraissent parfois très difficiles aux premiers abords, peuvent être résolus de manière très directe en utilisant le double comptage. Voici par exemple comment résoudre le problème suivant, qui n'est autre que le problème 2 de l'IMO 1998.

Voici un autre problème, d'un genre fort différent, qui peut également être résolu de cette manière. Il s'agit du problème 3 de l'IMO 1989.