Théorie > Combinatoire > Théorie des graphes
Prérequis
Résumé
Nous présentons dans ce chapitre la notion de graphe et expliquons comment des graphes peuvent être cachés derrière des problèmes divers et variés. Nous donnons ensuite quelques résultats concernant les graphes eulériens et les graphes planaires. Enfin, nous voyons en quoi le coloriage des graphes peut s'avérer utile et énonçons un résultat fondamental dans ce sujet : le théorème de Ramsey.
Ce chapitre a été écrit par N. Radu et mis en ligne le 8 décembre 2014.
1. Vocabulaire
Un graphe est un ensemble de sommets et d'arêtes reliant certains de ces sommets. La plupart du temps, on demande qu'il n'y ait pas plus d'une arête entre deux sommets et qu'il n'y ait pas de boucle (c'est-à-dire d'arête reliant un sommet à lui-même) : on parle alors de graphe simple. Un exemple de graphe simple est représenté ci-dessous. On dessine généralement un cercle pour chaque sommet, afin de mieux les visualiser, et on les numérote parfois pour mieux les désigner.
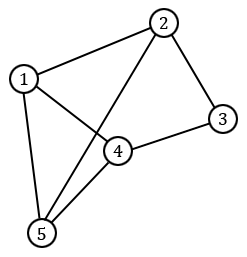
Il existe un certain nombre de mots de vocabulaire concernant les graphes. On dit par exemple que deux sommets sont adjacents s'ils sont reliés par une arête, on parle de chemin pour parler d'une succession d'arêtes dont deux consécutives partagent un sommet, ou encore de cycle pour parler d'un chemin dont le sommet de départ est égal au sommet d'arrivée. Lorsqu'un graphe est simple, on peut simplement désigner un chemin ou un cycle par ses sommets. Par exemple, sur notre graphe ci-dessus, on a $[1, 4, 3]$ qui est un chemin et $[5, 4, 3, 2, 5]$ qui est un cycle. On dit aussi qu'un graphe est connexe si deux sommets quelconques peuvent toujours être joints par un chemin (le graphe ci-dessus est connexe).
Un graphe particulier est le graphe complet à $n$ sommets. Il s'agit du graphe simple possédant $n$ sommets et toutes les $\frac{n(n-1)}{2}$ arêtes possibles entre ces $n$ sommets. On le note généralement $K_n$ et il est bien sûr connexe. Ci-dessous est représenté le graphe complet $K_5$.
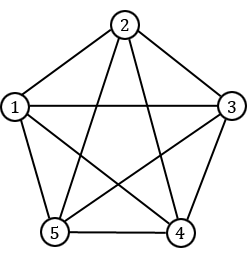
En pratique, il est rare de rencontrer un problème de combinatoire énoncé directement en termes de graphes. En fait, les graphes sont généralement cachés derrière un énoncé plus commun. Par exemple, si l'on parle de $n$ personnes, dont certaines sont amies et d'autres non (l'amitié étant réciproque), alors on peut facilement réexprimer le problème en termes de graphes. En effet, on peut représenter chaque personne par un sommet, et relier deux sommets si et seulement si les deux personnes correspondantes sont amies. On peut alors généralement écrire la thèse en termes de graphes également, et on est ainsi ramené à un problème de pure théorie des graphes.

Il existe un certain nombre de mots de vocabulaire concernant les graphes. On dit par exemple que deux sommets sont adjacents s'ils sont reliés par une arête, on parle de chemin pour parler d'une succession d'arêtes dont deux consécutives partagent un sommet, ou encore de cycle pour parler d'un chemin dont le sommet de départ est égal au sommet d'arrivée. Lorsqu'un graphe est simple, on peut simplement désigner un chemin ou un cycle par ses sommets. Par exemple, sur notre graphe ci-dessus, on a $[1, 4, 3]$ qui est un chemin et $[5, 4, 3, 2, 5]$ qui est un cycle. On dit aussi qu'un graphe est connexe si deux sommets quelconques peuvent toujours être joints par un chemin (le graphe ci-dessus est connexe).
Un graphe particulier est le graphe complet à $n$ sommets. Il s'agit du graphe simple possédant $n$ sommets et toutes les $\frac{n(n-1)}{2}$ arêtes possibles entre ces $n$ sommets. On le note généralement $K_n$ et il est bien sûr connexe. Ci-dessous est représenté le graphe complet $K_5$.

En pratique, il est rare de rencontrer un problème de combinatoire énoncé directement en termes de graphes. En fait, les graphes sont généralement cachés derrière un énoncé plus commun. Par exemple, si l'on parle de $n$ personnes, dont certaines sont amies et d'autres non (l'amitié étant réciproque), alors on peut facilement réexprimer le problème en termes de graphes. En effet, on peut représenter chaque personne par un sommet, et relier deux sommets si et seulement si les deux personnes correspondantes sont amies. On peut alors généralement écrire la thèse en termes de graphes également, et on est ainsi ramené à un problème de pure théorie des graphes.
Remarque
Nous avons ici donné la définition de graphe non-orienté, en ce sens que les arêtes n'ont pas d'orientation. On peut aussi définir les graphes orientés pour lesquels une arête du sommet $a$ vers le sommet $b$ n'est pas la même chose qu'une arête de $b$ vers $a$. On munit alors les arêtes de flèches pour distinguer leur sens. Nous continuerons à analyser les graphes non-orientés dans ce chapitre, mais certains résultats s'écrivent également pour les graphes orientés.
2. Graphes eulériens
Problème des sept ponts de Königsberg
Le problème suivant est très connu en mathématiques, et est réputé pour être à l'origine de la théorie des graphes.Problème des sept ponts de Königsberg
La ville de Königsberg est construite autour de deux îles situées sur le Pregel et reliées entre elles par un pont. Six autres ponts relient les rives de la rivière à l'une ou l'autre des deux îles, comme représentés sur le plan ci-dessous. Le problème consiste à déterminer s'il existe ou non une promenade dans les rues de Königsberg passant une et une seule fois par chaque pont de la ville.
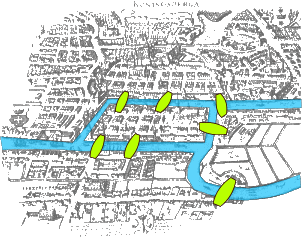

On peut facilement réécrire ce problème en termes de graphes, en prenant les quatre parcelles de terre pour sommets et les sept ponts pour arêtes. Le problème revient alors à déterminer s'il existe un chemin passant une et une seule fois par chaque arête dans le graphe suivant :
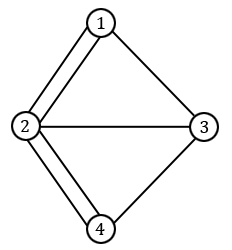
Comme souvent pour de tels problèmes, on se persuade vite que le problème est impossible par essais et erreurs, mais le tout est de le prouver. C'est Euler qui y est parvenu, avec l'idée suivante : si un tel chemin existait, alors pour chaque sommet différent de celui de départ et de celui d'arrivée, il serait possible de repartir du sommet à chaque fois que l'on y arrive. Autrement dit, le nombre d'arêtes partant d'un tel sommet doit toujours être pair. Pour cette raison, on introduit la notion de degré d'un sommet désignant le nombre d'arêtes partant de ce sommet, et l'impossibilité d'effectuer une promenade complète dans les rue de Königsberg vient alors du fait que les degrés des $4$ sommets du graphe sont impairs, alors qu'il en faudrait au moins deux de degré pair.
Chemin et cycle eulérien
Réexprimons ce problème pour un graphe quelconque. On parle de chemin eulérien dans un graphe pour désigner un chemin passant une et une seule fois par chaque arête. De la même façon, on définit un cycle eulérien comme étant un cycle passant exactement une fois par chaque arête (cela revient à demander que la promenade se termine là où elle a commencé). Le problème des ponts de Königsberg revient à déterminer s'il existe un chemin eulérien dans un graphe donné. En fait, Euler est parvenu à donner une condition nécessaire et suffisante sur le graphe pour qu'un chemin eulérien existe.Théorème (existence d'un chemin eulérien)
Soit $G$ un graphe non-orienté n'ayant aucun sommet isolé (c'est-à-dire de degré nul). Il existe un chemin eulérien dans $G$ si et seulement si $G$ est connexe et possède exactement zéro ou deux sommets de degré impair.
Démonstration
Commençons par le sens $\Rightarrow$. On suppose qu'il existe un chemin eulérien dans un certain graphe $G$. Tout d'abord, $G$ est clairement connexe puisque le chemin passe par toutes les arêtes et donc tous les sommets de $G$. Pour la condition sur les degrés, notons $v$ le sommet de départ et $w$ le sommet d'arrivée du chemin. Puisque le chemin passe par toutes les arêtes, on peut facilement compter les degrés de chaque sommet en suivant le chemin. En effet, on peut initialement mettre tous les degrés à $0$ et, à chaque fois que l'on passe par un sommet en suivant notre chemin, on augmente son degré de $2$ puisqu'il y a une arête arrivant en ce sommet et une arête en repartant. Cela ne sera juste pas pareil au départ du chemin et à l'arrivée : on incrémente le degré de $v$ uniquement de $1$ au départ et celui de $w$ de $1$ également à l'arrivée. Ainsi, si $v \neq w$, alors ce sont les deux seuls ayant un degré impair, alors que si $v = w$, tous les sommets sont de degré pair.
Le sens $\Leftarrow$ est un peu plus compliqué. On suppose en fait être en présence d'un graphe $G$ connexe et vérifiant la condition sur les degrés et on va donner une façon de construire un chemin eulérien dans $G$. Nous illustrerons cette démonstration sur le graphe suivant.
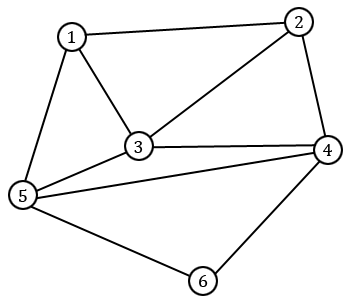
S'il existe exactement deux sommets de degré impair, alors on les note $v$ et $w$. Si par contre ils sont tous de degré pair, alors on prend $v = w$ quelconque. Sur notre exemple, on prend $v = 1$ et $w = 2$. Nous allons construire un chemin eulérien reliant $v$ à $w$. L'idée est en fait assez simple : on part de $v$ et on prend une arête quelconque partant de $v$, comme $[1,3]$ sur notre exemple. Au vu des degrés des différents sommets, il existe toujours au moins une arête non encore empruntée partant du sommet auquel on arrive, sauf éventuellement si on est en $w$. On prend donc une telle arête, comme $[3, 2]$ sur notre exemple, et on continue de la sorte jusqu'à ce qu'il ne soit plus possible d'avancer.
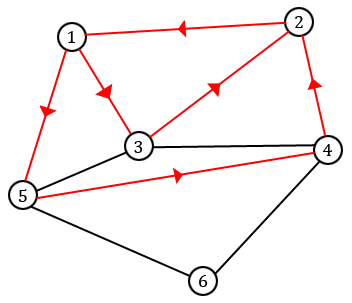
Au vu de nos remarques sur les degrés, le sommet final auquel on sera coincé sera toujours forcément $w$. On a donc jusqu'ici trouvé un chemin reliant $v$ à $w$. Il n'est cependant pas certain qu'il soit eulérien : on n'est peut-être pas passé par toutes les arêtes.
Cependant, si on "supprime" toutes les arêtes par lesquelles on est déjà passé, on remarque que le nouveau graphe obtenu n'a plus que des sommets de degré pair. On peut donc agrandir notre chemin en partant d'un sommet du chemin dont toutes les arêtes n'ont pas encore été empruntées (comme $3$ sur notre exemple), et en effectuant le même procédé que précédemment avec les arêtes restantes jusqu'à revenir au même sommet.
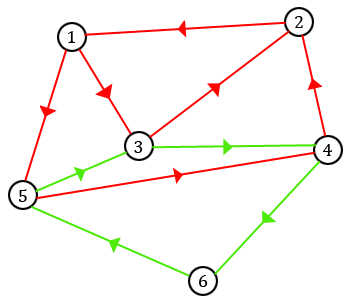
On prolonge alors notre chemin initial en lui incluant la boucle que nous venons de créer. Sur notre exemple, on peut ainsi obtenir le chemin
$$[1, 3, 4, 6, 5, 3, 2, 1, 5, 4, 2].$$ Si le chemin obtenu n'est toujours pas eulérien, alors on peut bien sûr continuer à rajouter des boucles jusqu'à ce que ce soit le cas. Le fait que notre graphe soit connexe nous assure que l'on arrivera ainsi à un chemin eulérien.
Le sens $\Leftarrow$ est un peu plus compliqué. On suppose en fait être en présence d'un graphe $G$ connexe et vérifiant la condition sur les degrés et on va donner une façon de construire un chemin eulérien dans $G$. Nous illustrerons cette démonstration sur le graphe suivant.

S'il existe exactement deux sommets de degré impair, alors on les note $v$ et $w$. Si par contre ils sont tous de degré pair, alors on prend $v = w$ quelconque. Sur notre exemple, on prend $v = 1$ et $w = 2$. Nous allons construire un chemin eulérien reliant $v$ à $w$. L'idée est en fait assez simple : on part de $v$ et on prend une arête quelconque partant de $v$, comme $[1,3]$ sur notre exemple. Au vu des degrés des différents sommets, il existe toujours au moins une arête non encore empruntée partant du sommet auquel on arrive, sauf éventuellement si on est en $w$. On prend donc une telle arête, comme $[3, 2]$ sur notre exemple, et on continue de la sorte jusqu'à ce qu'il ne soit plus possible d'avancer.

Au vu de nos remarques sur les degrés, le sommet final auquel on sera coincé sera toujours forcément $w$. On a donc jusqu'ici trouvé un chemin reliant $v$ à $w$. Il n'est cependant pas certain qu'il soit eulérien : on n'est peut-être pas passé par toutes les arêtes.
Cependant, si on "supprime" toutes les arêtes par lesquelles on est déjà passé, on remarque que le nouveau graphe obtenu n'a plus que des sommets de degré pair. On peut donc agrandir notre chemin en partant d'un sommet du chemin dont toutes les arêtes n'ont pas encore été empruntées (comme $3$ sur notre exemple), et en effectuant le même procédé que précédemment avec les arêtes restantes jusqu'à revenir au même sommet.

On prolonge alors notre chemin initial en lui incluant la boucle que nous venons de créer. Sur notre exemple, on peut ainsi obtenir le chemin
$$[1, 3, 4, 6, 5, 3, 2, 1, 5, 4, 2].$$ Si le chemin obtenu n'est toujours pas eulérien, alors on peut bien sûr continuer à rajouter des boucles jusqu'à ce que ce soit le cas. Le fait que notre graphe soit connexe nous assure que l'on arrivera ainsi à un chemin eulérien.
On a donc une condition nécessaire et suffisante pour qu'il existe un chemin eulérien dans un graphe. Au vu de la démonstration donnée, on remarque que ce chemin est en fait un cycle si et seulement si il n'y a aucun sommet de degré impair.
Théorème (existence d'un cycle eulérien)
Soit $G$ un graphe non-orienté n'ayant aucun sommet isolé (c'est-à-dire de degré nul). Il existe un cycle eulérien dans $G$ si et seulement si $G$ est connexe et ne possède que des sommets de degré pair.
Losqu'il existe un cycle eulérien dans un graphe, on dit tout simplement qu'il s'agit d'un graphe eulérien.
3. Graphes planaires
Énigme des trois maisons
L'énigme des trois maisons consiste à résoudre le problème suivant.Énigme des trois maisons
On a trois maisons (numérotées $1$, $2$ et $3$), représentées en bas de la figure suivante, et trois usines, représentées en haut. La première usine fournit de l'eau, la deuxième du gaz et la troisième de l'électricité. On désire relier chacune des trois maisons aux trois usines pour qu'elles aient accès à l'eau, au gaz et à l'électricité. Une contrainte supplémentaire est que les tuyaux ne doivent jamais se croiser.


Ce problème peut se réécrire en termes de théorie des graphes. On a déjà les six sommets, et on cherche à relier chaque sommet du bas à chaque sommet du haut par une arête, de sorte qu'aucune arête n'en croise une autre. On définit alors un graphe planaire comme étant un graphe qui peut être représenté dans le plan sans qu'aucune arête n'en croise une autre. Par exemple, le graphe suivant est planaire :
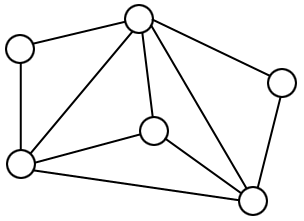
L'énigme des trois maisons consiste alors à représenter le graphe suivant, noté $K_{3,3}$, sans qu'aucune arête ne croise une autre, pourvu bien sûr que ce soit faisable, c'est-à-dire qu'il soit planaire.
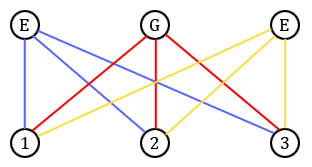
Après plusieurs essais (essayez !), il semble difficile de résoudre cette énigme. Serait-il possible que ce graphe ne soit pas planaire et qu'il n'existe donc pas de solution à l'énigme ? Pour le voir, nous aurons besoin de la formule d'Euler.
Formule d'Euler
La formule d'Euler est une relation entre le nombre de sommets, le nombre d'arêtes et le nombre de faces d'un graphe connexe planaire. Une face d'un graphe planaire est simplement une zone du plan délimitée par des arêtes. Lorsqu'on compte le nombre de faces d'un graphe planaire, il ne faut pas oublier la face extérieure (celle qui est infinie). Sur l'exemple de graphe planaire donné plus haut, on a $6$ sommets, $10$ arêtes et $6$ faces.Formule d'Euler
Dans un graphe planaire connexe, on a toujours
$$s-a+f = 2,$$ où $s$ représente le nombre de sommets, $a$ le nombre d'arêtes et $f$ le nombre de faces du graphe.
$$s-a+f = 2,$$ où $s$ représente le nombre de sommets, $a$ le nombre d'arêtes et $f$ le nombre de faces du graphe.
Cette formule est bien vérifiée sur notre exemple puisque $6-10+6 = 2$.
Démonstration
Un graphe connexe peut être obtenu en partant du graphe avec un seul sommet et aucune arête et en rajoutant des arêtes une par une, partant d'un sommet déjà existant et arrivant vers un sommet soit déjà existant, soit nouveau. Au départ, on a $1$ sommet, $0$ arête et $1$ faces, et la relation $1-0+1 = 2$ est bien vérifiée. Il suffit donc de montrer qu'à chaque fois que l'on rajoute une arête (et éventuellement le sommet d'arrivée avec s'il n'existait pas encore), la valeur de $s-a+f$ reste inchangée. Deux cas de figure se présentent lorsqu'on rajoute une arête :
- Si le sommet d'arrivée de l'arête n'existe pas encore, alors on le rajoute en même temps que l'arête. En rajoutant cette arête et ce sommet, le nombre de faces reste inchangé (puisque la nouvelle arête ne coupe aucune face en deux). On a donc $s$ qui devient $(s+1)$ et $a$ qui devient $(a+1)$, et la valeur de $s-a+f$ ne change pas.
- Si le sommet d'arrivée de l'arête existe déjà, alors on ne rajoute aucun sommet. Par contre, la nouvelle arête coupe toujours une face en deux. Dans ce cas, $a$ devient donc $(a+1)$ et $f$ devient $(f+1)$, ce qui laisse à nouveau la valeur de $s-a+f$ inchangée.
On peut utiliser la formule d'Euler pour montrer que le graphe $K_{3,3}$ n'est pas planaire, c'est-à-dire que l'énigme des trois maisons ne possède en fait pas de solution.
Théorème (solution de l'énigme des trois maisons)
Le graphe $K_{3,3}$ n'est pas planaire.
Démonstration
Supposons par l'absurde que le graphe $K_{3,3}$ est planaire. Celui-ci possède $s = 6$ sommets et $a = 9$ arêtes, et la formule d'Euler nous dit que le nombre de faces est forcément égal à
$$f = 2-s+a = 2-6+9 = 5.$$ Or, chaque face possède au moins $4$ arêtes. En effet, il n'est pas possible d'avoir une face avec $3$ arêtes puisqu'une arête relie toujours un sommet du bas à un sommet du haut (et pour avoir un cycle, il faut donc un nombre pair d'arêtes). Puisque chaque arête intervient dans exactement deux faces différentes, on ne peut, avec $9$ arêtes, qu'avoir au plus
$$\frac{9}{4} \cdot 2 = 4,\!5 \text{ faces}.$$ On arrive donc à une contradiction puisque $4,\!5 < 5$.
$$f = 2-s+a = 2-6+9 = 5.$$ Or, chaque face possède au moins $4$ arêtes. En effet, il n'est pas possible d'avoir une face avec $3$ arêtes puisqu'une arête relie toujours un sommet du bas à un sommet du haut (et pour avoir un cycle, il faut donc un nombre pair d'arêtes). Puisque chaque arête intervient dans exactement deux faces différentes, on ne peut, avec $9$ arêtes, qu'avoir au plus
$$\frac{9}{4} \cdot 2 = 4,\!5 \text{ faces}.$$ On arrive donc à une contradiction puisque $4,\!5 < 5$.
Formule d'Euler pour les polyèdres
La formule d'Euler est également vraie pour les polyèdres convexes. Cela peut sembler être un hasard, mais il est en fait possible de passer d'un polyèdre à un graphe planaire avec un peu d'astuce.Formule d'Euler pour les polyèdres
Dans un polyèdre convexe dans l'espace, on a toujours
$$s-a+f = 2,$$ où $s$ représente le nombre de sommets, $a$ le nombre d'arêtes et $f$ le nombre de faces du polyèdre.
$$s-a+f = 2,$$ où $s$ représente le nombre de sommets, $a$ le nombre d'arêtes et $f$ le nombre de faces du polyèdre.
Idée de la démonstration
Il suffit en fait, à partir d'un polyèdre convexe, de construire un graphe planaire avec le même nombre d'arêtes, de sommets et de faces. L'idée est en fait assez simple. Considérons un certain polyèdre convexe. Pour construire un graphe planaire, on peut simplement poser le polyèdre sur une surface plane, "percer un trou" au milieu d'une des faces du polyèdre (de préférence une face en haut) et élargir ce trou jusqu'à "déplier" le polyèdre et l'aplatir sur la surface plane. On obtient ainsi un graphe planaire avec exactement le même nombre de sommets, d'arêtes et de faces, et on peut utiliser la formule d'Euler pour les graphes planaires. Notez que la face "percée" devient la face infinie du graphe.
Il s'agit là de l'intuition de la démonstration, mais celle-ci peut en fait être facilement rendue rigoureuse. Nous ne le faisons pas ici car cela demande la connaissance de la projection stéréographique.
4. Théorème de Ramsey
Coloration de graphes
Il arrive que l'on veuille naturellement colorier les différentes arêtes d'un graphe. Considérons par exemple le problème suivant.Problème
Dans une petite classe de six étudiants, certains élèves sont amis et d'autres non. La relation d'amitié est réciproque : si $A$ est ami avec $B$, alors $B$ est ami avec $A$. Montrer qu'il existe trois étudiants qui sont deux à deux amis ou trois étudiants qui sont deux à deux non amis.
Comme suggéré dans une section précédente, on peut écrire ce problème en termes de graphes, en prenant $6$ sommets pour les six étudiants et en reliant deux étudiants dès qu'ils sont amis. Il faut alors prouver que soit il existe un triangle dans le graphe (ce qui signifierait que les étudiants correspondants sont deux à deux amis), soit il existe trois sommets non reliés (ce qui donnerait trois étudiants non amis). La thèse semblait cependant à peu près symétrique au départ et ne l'est plus vraiment en termes de graphes.
Une autre façon de traduire ce problème est de relier toutes les paires de sommets, mais de donner une couleur différente aux arêtes selon que les étudiants concernés sont amis ou non. On peut donc décider de relier des sommets en vert si les étudiants sont amis et en rouge s'ils ne le sont pas. On se retrouve ainsi avec le graphe complet $K_6$ pour lequel chaque arête est coloriée en vert ou en rouge, et le problème consiste à montrer qu'il existe au moins un triangle monochromatique (c'est-à-dire d'une seule couleur) dans le graphe. Sur la figure suivante, on est presque parvenu à trouver un contre-exemple, mais il existe bel et bien un triangle monochromatique (il y en a même deux : un vert et un rouge).
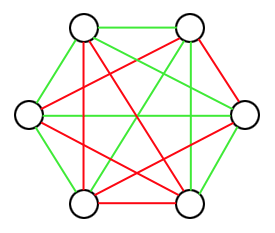
Ce problème est en fait facile à résoudre en faisant bon usage du principe des tiroirs. Procédons par l'absurde en supposant avoir trouvé une coloration de $K_6$ sans aucun triangle monochromatique. On considère alors un sommet quelconque $S$ de ce graphe. De ce sommet partent $5$ arêtes, chacune de couleur verte ou rouge. Par le principe des tiroirs, il y a forcément $3$ de ces arêtes qui sont de la même couleur (on met $5$ chaussettes (les arêtes) dans $2$ tiroirs (les couleurs) : il y a toujours un tiroir contenant $3$ chaussettes). Disons sans perte de généralité que l'on a $3$ arêtes rouges partant de $S$, et qu'elles aboutissent aux sommets $A$, $B$ et $C$. Vu que les arêtes $[S,A]$ et $[S, B]$ sont rouges, l'arête $[A,B]$ est verte (sinon, le triangle $SAB$ serait entièrement rouge). De la même façon, l'arête $[A,C]$ est verte de sorte que $SAC$ ne soit pas entièrement rouge et l'arête $[B, C]$ également de sorte que $SBC$ ne soit pas monochromatique. Mais alors, le triangle $ABC$ est entièrement vert ! Nous avons trouvé une contradiction : il n'est donc pas possible de colorier $K_6$ avec deux couleurs de sorte que l'on ait aucun triangle monochromatique.
Théorème de Ramsey
Ce problème peut être fortement généralisé. On peut en effet considérer le graphe complet $K_N$ pour $N$ quelconque et le colorier avec $c$ couleurs $1, 2, \ldots, c$. Aussi, au lieu de se demander s'il existe un triangle d'une seule couleur, on peut se demander s'il existe un sous-graphe complet $K_{n_i}$ (on parle alors d'une $n_i$-clique) entièrement de la couleur $i$ (pour $n_i$ quelconque dépendant éventuellement de $i$). Notre problème ci-dessus correspondrait alors au cas particulier où $N = 6$, $c = 2$ et $n_1 = n_2 = 3$.Le théorème de Ramsey nous dit que, quelles que soient les valeurs de $c$ et de $n_1, \ldots, n_c$, il existe toujours un certain $N$ à partir duquel il est impossible de colorier $K_N$ avec $c$ couleurs sans qu'il n'y ait de $n_i$-clique entièrement de la couleur $i$ pour un $i \in \{1, \ldots, c\}$.
Théorème de Ramsey
Soit $c \in \mathbb{N}_0$ et $n_1, \ldots, n_c \in \mathbb{N}_0$. Il existe un entier $N \in \mathbb{N}_0$ tel que pour toute coloration de $K_N$ avec $c$ couleurs (notées $1,2, \ldots, c$), il existe une couleur $i$ et une $n_i$-clique de $K_N$ entièrement de la couleur $i$. Le plus petit $N$ vérifiant cette condition est noté $R(n_1, \ldots, n_c)$ et est appelé nombre de Ramsey.
Ce résultat se montre par récurrence mais nous ne donnons pas la démonstration ici.
Valeurs des nombres de Ramsey
En montrant que, pour tout coloriage de $K_6$ avec deux couleurs, il existe toujours un triangle monochromatique, on a montré que $R(3,3) \leq 6$. En fait, il n'est pas difficile de montrer qu'on a $R(3,3) = 6$ : il suffit de donner un coloriage de $K_5$ ne contenant aucun triangle monochromatique, comme par exemple le suivant.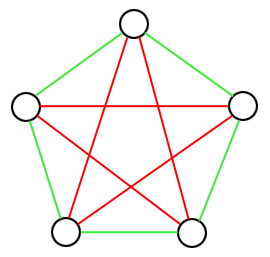
Les nombres de Ramsey ne sont pas bien connus. Par exemple, pour deux couleurs, on ne connait précisément les valeurs de $R(n, m)$ que pour les petites valeurs de $n$ et $m$. Pour des valeurs plus grandes, on ne connait qu'un intervalle dans lequel $R(n, m)$ se situe. En fait, savoir que $R(n, m) \in [a, b]$ signifie deux choses :
- Il existe un coloriage en vert et rouge de $K_{a-1}$ ne contenant aucune $n$-clique entièrement verte et aucune $m$-clique entièrement rouge,
- Il n'existe aucun tel coloriage de $K_b$.
Valeurs des premiers nombres de Ramsey
Les premières valeurs de $R(n, m)$ sont données dans le tableau suivant :
$$\begin{array}{c|cccccccc}
& 1 & 2 & 3 & 4 & 5 & 6 & 7 \\
\hline
1 & 1 & & & & & & \\
2 & 1 & 2 & & & & & \\
3 & 1 & 3 & 6 & & & & \\
4 & 1 & 4 & 9 & 18 & & & \\
5 & 1 & 5 & 14 & 25 & [43,49] & & \\
6 & 1 & 6 & 18 & [36,41] & [58,87] & [102, 165] & \\
7 & 1 & 7 & 23 & [49,61] & [80,143] & [113, 298] & [205, 540]
\end{array}$$
$$\begin{array}{c|cccccccc}
& 1 & 2 & 3 & 4 & 5 & 6 & 7 \\
\hline
1 & 1 & & & & & & \\
2 & 1 & 2 & & & & & \\
3 & 1 & 3 & 6 & & & & \\
4 & 1 & 4 & 9 & 18 & & & \\
5 & 1 & 5 & 14 & 25 & [43,49] & & \\
6 & 1 & 6 & 18 & [36,41] & [58,87] & [102, 165] & \\
7 & 1 & 7 & 23 & [49,61] & [80,143] & [113, 298] & [205, 540]
\end{array}$$