Théorie > Combinatoire > Invariants et (mono)variants
Prérequis
Aucun prérequis.
Résumé
Bien que la notion d'invariant soit assez simple à comprendre, elle reste un outil très puissant pour résoudre des problèmes de combinatoire. De manière un peu plus générale, on peut également utiliser des monovariants ou des variants pour mieux comprendre certaines situations non évidentes.
Ce chapitre a été écrit par N. Radu et mis en ligne le 8 décembre 2014.
1. Invariants
Les invariants permettent de résoudre des problèmes dans lesquels une tâche, une opération ou une transformation est répétée un certain nombre de fois (éventuellement une infinité). Un invariant est, dans une telle situation, une quantité qui ne varie pas lors de la transformation. Pour bien comprendre comment ceux-ci fonctionnent, examinons deux exemples différents.
Ce raisonnement, bien qu'achevant le problème, n'est pas très joli et peut très vite être erroné. De plus, il fonctionne ici car il n'y a que six secteurs, mais il aurait par exemple été bien plus difficile à appliquer s'il y avait eu $2014$ secteurs. En fait, il était possible de résoudre le problème très rapidement en utilisant un invariant.
Le problème suivant est un autre exemple où un invariant permet de conclure directement :
Problème
Un cercle est divisé en $6$ secteurs. Quatre d'entre eux contiennent le nombre $0$ et les deux autres le nombre $1$, de la manière indiquée sur la figure suivante. On peut augmenter de une unité le contenu de deux cases voisines. Peut-on atteindre un état où les contenus des cases sont tous égaux ?


Solution fastidieuse
Pour résoudre un tel problème, on commence bien sûr par essayer d'obtenir six nombres égaux. Il ne faut que peu de temps pour se convaincre que cela est en fait impossible. L'approche la plus intuitive pour résoudre ce problème est peut-être la suivante. On observe tout d'abord qu'il n'y a que six opérations possibles (il n'y a que six choix différents de deux cases voisines), et que l'ordre dans lequel on effectue les opérations n'a aucune importance. On peut alors procéder par l'absurde et supposer qu'il existe une suite d'opérations amenant à un état où les six nombres sont égaux. On numérote $1, \ldots, 6$ les six secteurs (de sorte que les secteurs $1$ et $3$ contiennent le chiffre $1$) et on note $n_1$ le nombre de fois que l'on a incrémenté les cases $1$ et $2$, $n_2$ le nombre de fois que l'on a incrémenté les cases $2$ et $3$, et ainsi de suite jusque $n_6$, le nombre de fois que l'on a incrémenté les cases $6$ et $1$. Le fait que les six valeurs sont égales après ces opérations s'écrit alors
$$1+n_6+n_1 = n_1+n_2 = 1+n_2+n_3 = n_3+n_4 = n_4+n_5 = n_5+n_6.$$ Il ne reste alors plus qu'à trouver une absurdité pour conclure que c'est impossible. En fait, on peut par exemple remarquer que certaines de ces égalités impliquent
$$n_6+1 = n_2,$$ $$n_2+1 = n_4,$$ $$n_4 = n_6,$$ ce qui est impossible (en additionnant les trois égalités, on trouve $2 = 0$).
$$1+n_6+n_1 = n_1+n_2 = 1+n_2+n_3 = n_3+n_4 = n_4+n_5 = n_5+n_6.$$ Il ne reste alors plus qu'à trouver une absurdité pour conclure que c'est impossible. En fait, on peut par exemple remarquer que certaines de ces égalités impliquent
$$n_6+1 = n_2,$$ $$n_2+1 = n_4,$$ $$n_4 = n_6,$$ ce qui est impossible (en additionnant les trois égalités, on trouve $2 = 0$).
Ce raisonnement, bien qu'achevant le problème, n'est pas très joli et peut très vite être erroné. De plus, il fonctionne ici car il n'y a que six secteurs, mais il aurait par exemple été bien plus difficile à appliquer s'il y avait eu $2014$ secteurs. En fait, il était possible de résoudre le problème très rapidement en utilisant un invariant.
Solution avec un invariant
L'idée est de noter $x_1, \ldots, x_6$ les valeurs des nombres dans les six secteurs (disons avec $x_1 = x_3 = 1$ au départ), et de trouver une fonction de ces $x_1, \ldots, x_6$ ayant la propriété qu'elle ne change pas lorsqu'on effectue une opération. Les opérations consistant à incrémenter les valeurs de deux $x_i$ consécutifs, l'invariant le plus naturel est
$$X = x_1 - x_2 + x_3 - x_4 + x_5 - x_6.$$ En effet, à chaque fois que l'on augmente $x_i$ et $x_{i+1}$ pour un certain $i$ (ou $x_6$ et $x_1$), la valeur de $X$ ne change pas. Il s'agit donc bien d'un invariant du problème. Il reste alors à constater que $X = 2$ dans la configuration initiale, ce qui signifie que quelles que soient les opérations que l'on effectue sur nos secteurs, la valeur de $X$ restera toujours égale à $2$. Or, nous nous demandons s'il est possible d'atteindre un état où $x_1 = \ldots = x_6$. Dans un tel état, la valeur de $X$ est égale à $0$, donc nous venons de montrer qu'on ne parviendra jamais à égaliser les six nombres.
$$X = x_1 - x_2 + x_3 - x_4 + x_5 - x_6.$$ En effet, à chaque fois que l'on augmente $x_i$ et $x_{i+1}$ pour un certain $i$ (ou $x_6$ et $x_1$), la valeur de $X$ ne change pas. Il s'agit donc bien d'un invariant du problème. Il reste alors à constater que $X = 2$ dans la configuration initiale, ce qui signifie que quelles que soient les opérations que l'on effectue sur nos secteurs, la valeur de $X$ restera toujours égale à $2$. Or, nous nous demandons s'il est possible d'atteindre un état où $x_1 = \ldots = x_6$. Dans un tel état, la valeur de $X$ est égale à $0$, donc nous venons de montrer qu'on ne parviendra jamais à égaliser les six nombres.
Le problème suivant est un autre exemple où un invariant permet de conclure directement :
Problème
Les nombres $1, 2, \ldots, 1974$ sont écrits sur un tableau. On peut remplacer deux quelconques de ces nombres par leur somme ou par leur différence. Peut-on obtenir le nombre $0$ après avoir répété cette opération $1973$ fois ?
Solution
Vu qu'une opération consiste à remplacer deux nombres par leur somme, un invariant envisageable est
$$X = \text{somme des éléments écrits sur le tableau.}$$ Bien sûr, lorsque l'on remplace deux éléments par leur somme, la valeur de $X$ ne change pas. Malheureusement, ce n'est pas le cas lorsque l'on remplace deux éléments par leur différence. En effet, si on remplace les deux nombres $a$ et $b$ (avec $a \geq b$) par leur différence $(a-b)$, la valeur de $X$ diminue de $a+b-(a-b) = 2b$. On constate cependant par ce calcul que $2b$ est toujours pair, ce qui signifie que la valeur de $X$, même si elle change, ne changera jamais de parité ! On peut donc remplacer notre invariant potentiel $X$ par
$$Y = \text{parité de la somme des éléments écrits sur le tableau.}$$ Nous avons montré que $Y$ était bel et bien un invariant du problème. Or, au départ, la somme des éléments est égale à
$$1+2+\ldots+1974 = \frac{1974\cdot1975}{2} = 987 \cdot 1975,$$ ce qui signifie que la valeur de $Y$ est "impair" dans la configuration initiale. Après $1973$ opérations, le nombre que l'on obtiendra sur le tableau sera donc toujours impair, ce qui signifie qu'il ne pourra jamais être nul.
$$X = \text{somme des éléments écrits sur le tableau.}$$ Bien sûr, lorsque l'on remplace deux éléments par leur somme, la valeur de $X$ ne change pas. Malheureusement, ce n'est pas le cas lorsque l'on remplace deux éléments par leur différence. En effet, si on remplace les deux nombres $a$ et $b$ (avec $a \geq b$) par leur différence $(a-b)$, la valeur de $X$ diminue de $a+b-(a-b) = 2b$. On constate cependant par ce calcul que $2b$ est toujours pair, ce qui signifie que la valeur de $X$, même si elle change, ne changera jamais de parité ! On peut donc remplacer notre invariant potentiel $X$ par
$$Y = \text{parité de la somme des éléments écrits sur le tableau.}$$ Nous avons montré que $Y$ était bel et bien un invariant du problème. Or, au départ, la somme des éléments est égale à
$$1+2+\ldots+1974 = \frac{1974\cdot1975}{2} = 987 \cdot 1975,$$ ce qui signifie que la valeur de $Y$ est "impair" dans la configuration initiale. Après $1973$ opérations, le nombre que l'on obtiendra sur le tableau sera donc toujours impair, ce qui signifie qu'il ne pourra jamais être nul.
2. Monovariants
Un monovariant est, comme un invariant, une quantité que l'on peut calculer à chaque étape. La différence est que sa valeur n'est plus invariante au cours du temps, mais varie de manière monotone (c'est-à-dire croissante ou décroissante). Un monovariant peut par exemple servir pour montrer qu'un processus se termine toujours, comme dans l'exemple suivant.
Problème
Étant donnés $2n$ points distincts du plan, prouver que l'on peut toujours les relier deux par deux par $n$ segments disjoints.
Solution
Ce problème peut sembler a priori très compliqué : comment trouver en toute généralité une façon de relier les $2n$ points sans que les différents segments ne se croisent ? Une façon de faire est de d'abord relier les points deux par deux de manière quelconque, sans se soucier des croisements éventuels, et de tenter de "défaire" tous les croisements que l'on a ainsi créé. On peut par exemple, dès que les segments $[AB]$ et $[CD]$ se croisent, les remplacer par les segments $[AC]$ et $[BD]$ comme sur la figure suivante :
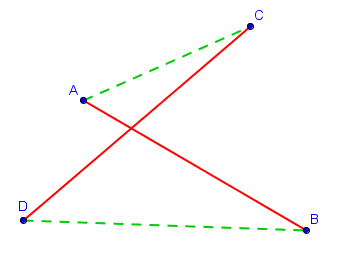
Il reste à montrer qu'à force de défaire les croisements de cette manière, on arrivera toujours à une situation pour laquelle il n'y a plus de croisements. Le monovariant naturel que l'on désire considérer est donc simplement
$$X = \text{nombre de croisements.}$$ La valeur de $X$ est au départ un nombre entier positif et on désire arriver à une situation où $X = 0$. Puisqu'à chaque "décroisement", la valeur de $X$ semble diminuer de $1$, on serait tenté de conclure que notre méthode de "décroisements" successifs aboutira toujours. Ce raisonnement est cependant erroné ! En effet, la valeur de $X$ ne diminue pas forcément à chaque "décroisement", puisqu'il se peut très bien que l'on ait créé de nouveaux croisements en décroisant les deux qui nous intéressaient, comme sur la figure suivante :
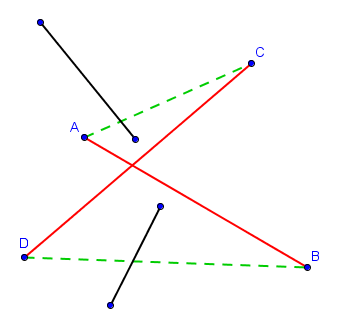
Notre $X$ n'est donc pas un monovariant, puisque sa valeur peut très bien augmenter. Il faut donc trouver quelque chose de plus subtil.
Il n'est pas évident d'y penser, mais un monovariant adéquat dans cette situation est en fait
$$Y = \text{somme des longueurs des $n$ segments.}$$ En effet, lorsque les quatre points $A, B, C, D$ ne sont pas alignés (comme sur nos figures), remplacer $[AB]$ et $[CD]$ (lorsqu'ils se croisent) par $[AC]$ et $[BD]$ diminuera toujours la longueur totale des segments. Il suffit pour le vérifier d'utiliser l'inégalité triangulaire : en notant $E$ l'intersection de $[AB]$ et $[CD]$, on trouve que
$$|AC| + |BD| < |AE| + |EC| + |BE| + |ED| = |AB| + |CD|.$$ Dans le cas où $A, B, C$ et $D$ sont alignés (dans un ordre tel que $[AB]$ et $[CD]$ se croisent), on peut simplement les remplacer par le segment formé des deux "premiers" points et le segment formé par les deux "derniers" points. Là aussi dans tous les cas la somme des longueurs des segments diminue strictement. Notre $Y$ est donc bel et bien un monovariant puisqu'il décroît strictement à chaque fois que l'on défait un croisement.
Ce monovariant implique qu'on ne passera jamais deux fois par la même configuration en décroisant ainsi des segments successivement. Or, il n'existe qu'un nombre fini de manières de relier les $2n$ points par $n$ segments (il y a en fait $(2n-1) \cdot (2n-3) \cdot \ldots \cdot 3\cdot 1$ configurations). Cela signifie que notre processus de décroisement va finir par s'arrêter, et on sera alors dans une situation sans aucun croisement ! Il existe donc bel et bien une façon de relier les $2n$ points par $n$ segments disjoints.

Il reste à montrer qu'à force de défaire les croisements de cette manière, on arrivera toujours à une situation pour laquelle il n'y a plus de croisements. Le monovariant naturel que l'on désire considérer est donc simplement
$$X = \text{nombre de croisements.}$$ La valeur de $X$ est au départ un nombre entier positif et on désire arriver à une situation où $X = 0$. Puisqu'à chaque "décroisement", la valeur de $X$ semble diminuer de $1$, on serait tenté de conclure que notre méthode de "décroisements" successifs aboutira toujours. Ce raisonnement est cependant erroné ! En effet, la valeur de $X$ ne diminue pas forcément à chaque "décroisement", puisqu'il se peut très bien que l'on ait créé de nouveaux croisements en décroisant les deux qui nous intéressaient, comme sur la figure suivante :

Notre $X$ n'est donc pas un monovariant, puisque sa valeur peut très bien augmenter. Il faut donc trouver quelque chose de plus subtil.
Il n'est pas évident d'y penser, mais un monovariant adéquat dans cette situation est en fait
$$Y = \text{somme des longueurs des $n$ segments.}$$ En effet, lorsque les quatre points $A, B, C, D$ ne sont pas alignés (comme sur nos figures), remplacer $[AB]$ et $[CD]$ (lorsqu'ils se croisent) par $[AC]$ et $[BD]$ diminuera toujours la longueur totale des segments. Il suffit pour le vérifier d'utiliser l'inégalité triangulaire : en notant $E$ l'intersection de $[AB]$ et $[CD]$, on trouve que
$$|AC| + |BD| < |AE| + |EC| + |BE| + |ED| = |AB| + |CD|.$$ Dans le cas où $A, B, C$ et $D$ sont alignés (dans un ordre tel que $[AB]$ et $[CD]$ se croisent), on peut simplement les remplacer par le segment formé des deux "premiers" points et le segment formé par les deux "derniers" points. Là aussi dans tous les cas la somme des longueurs des segments diminue strictement. Notre $Y$ est donc bel et bien un monovariant puisqu'il décroît strictement à chaque fois que l'on défait un croisement.
Ce monovariant implique qu'on ne passera jamais deux fois par la même configuration en décroisant ainsi des segments successivement. Or, il n'existe qu'un nombre fini de manières de relier les $2n$ points par $n$ segments (il y a en fait $(2n-1) \cdot (2n-3) \cdot \ldots \cdot 3\cdot 1$ configurations). Cela signifie que notre processus de décroisement va finir par s'arrêter, et on sera alors dans une situation sans aucun croisement ! Il existe donc bel et bien une façon de relier les $2n$ points par $n$ segments disjoints.
3. Variants
Lorsqu'une fonction du problème semble intéressante, il n'est pas forcé qu'il s'agisse d'un invariant ou d'un monovariant pour qu'elle soit utile. En effet, la simple connaissance de comment elle varie peut parfois permettre d'avancer dans la résolution du problème. Pour illustrer cela, nous donnons la résolution du problème suivant, provenant de la Shortlist de l'IMO 2011 (il s'agit donc d'un problème qui aurait pu être posé à l'Olympiade Internationale, celui-ci n'est pas évident). Il ne s'agit pas d'un problème où une transformation est répétée, mais la technique utilisée pour le résoudre laisse fortement penser à celles que nous avons utilisées dans les sections précédentes. Les invariants et (mono)variants peuvent donc être subtilement cachés dans des problèmes de toute sorte.
Problème (Shortlist IMO 2011)
Supposons que $1000$ étudiants sont disposés en cercle. Prouver qu'il existe un entier $k$ avec $100 \leq k \leq 300$ tel qu'il existe un groupe contigu de $2k$ étudiants dont la première moitié contient autant de filles que la deuxième moitié.
Solution
Nous introduisons les variables $a_1, \ldots, a_{1000}$ qui représentent chacune un étudiant et vaut $1$ si celui-ci est une fille et $0$ sinon. On ne le dira plus, mais les indices supérieurs à $1000$ seront considérés modulo $1000$ (autrement dit, $a_{1001} = a_1$, $a_{1002} = a_2$,...) puisque les étudiants sont placés en cercle.
Nous notons alors
$$N(n, k) = a_n + \ldots + a_{n+k-1} - a_{n+k} - \ldots - a_{n+2k-1}.$$ L'intérêt de cette fonction $N(n, k)$ est qu'elle vaut $0$ exactement lorsque le groupe contigu de $2k$ personnes commençant en $a_n$ vérifie la thèse de l'énoncé. On procède donc, comme souvent, par l'absurde, en supposant que $N(n, k)$ ne vaut jamais $0$ pour $k \in [100, 300]$.
Notre idée est que, quand on passe d'un groupe contigu de $2k$ personnes au groupe contigu de $2k$ personnes juste décalé d'une personne, le nombre de filles ne change pas beaucoup. Autrement dit, les valeurs de $N(n, k)$ et $N(n+1, k)$ doivent être proches. En fait, on voit aisément que
$$N(n+1, k) - N(n, k) = -a_n + 2a_{n+k} - a_{n+2k}.$$ Cette valeur est toujours dans l'intervalle $[-2, 2]$. Pour $k$ fixé, on connaît donc assez bien comment $N(n, k)$ varie lorsque $n$ varie. On aimerait donc analyser la suite (qui forme un cycle)
$$N(1, k), \quad N(2, k), \quad \ldots, \quad N(1000, k).$$ Une remarque intéressante est que la somme de ces $1000$ nombres est nulle ! En effet, chaque $a_i$ apparaît $k$ fois positivement et $k$ fois négativement dans ces termes. On a donc un cycle de $1000$ nombres dont la somme vaut $0$ et tel que $N(n+1, k) - N(n, k) \in [-2, 2]$ pour tout $n$. On fixe maintenant $k = 100$ et on en déduit, les termes ne pouvant tous être du même signe, qu'il existe un certain $n_0$ tel que
$$N(n_0, 100) = 1 \quad \text{et} \quad N(n_0+1, 100) = -1.$$ Rappelons que nous cherchons une absurdité, c'est-à-dire certainement des valeurs de $n$ et $k$ telles que $N(n, k) = 0$. Nous en sommes proches puisque nous avons trouvé $-1$ et $1$. Examinons ce que ces valeurs représentent. Au vu de la relation exhibée plus haut, elles impliquent $a_{n_0} = a_{n_0 + 200} = 1$ et $a_{n_0 + 100} = 0$. Autrement dit, la situation est la suivante :
$$1, a_{n_0+1}, \ldots, a_{n_0+99}, 0, a_{n_0+101}, \ldots, a_{n_0+199}, 1$$ avec $a_{n_0+1} + \ldots + a_{n_0+99} = a_{n_0+101} + \ldots + a_{n_0+199}$. Nous n'avons jusqu'ici utilisé que la valeur $k = 100$, mais rappelons-nous qu'elle peut aller jusque $300$.
Nous avons donné $201$ étudiants ci-dessus, et en considérant ceux-ci et le suivant, on voit que ce suivant doit être une fille pour avoir $N(n_0, 101) \neq 0$. Similairement, l'élève précédant ces $201$ étudiants doit être une fille, d'où on a
$$1, 1, a_{n_0+1}, \ldots, a_{n_0+99}, 0, a_{n_0+101}, \ldots, a_{n_0+199}, 1, 1.$$ On peut alors utiliser $k = 102$ pour trouver que les deux autres étudiants aux extrémités sont également des filles, et ainsi de suite jusque $k = 300$ ce qui nous donne finalement
$$\underbrace{1, \ldots, 1}_{200 \text{ fois}}, 1, a_{n_0+1}, \ldots, a_{n_0+99}, 0, a_{n_0+101}, \ldots, a_{n_0+199}, 1, \underbrace{1, \ldots, 1}_{200 \text{ fois}}.$$ On a donc trouvé $200$ filles consécutives, c'est-à-dire un bloc de $200$ étudiants dont la première moitié contient autant de filles que la deuxième : c'est une absurdité et cela termine le problème.
Nous notons alors
$$N(n, k) = a_n + \ldots + a_{n+k-1} - a_{n+k} - \ldots - a_{n+2k-1}.$$ L'intérêt de cette fonction $N(n, k)$ est qu'elle vaut $0$ exactement lorsque le groupe contigu de $2k$ personnes commençant en $a_n$ vérifie la thèse de l'énoncé. On procède donc, comme souvent, par l'absurde, en supposant que $N(n, k)$ ne vaut jamais $0$ pour $k \in [100, 300]$.
Notre idée est que, quand on passe d'un groupe contigu de $2k$ personnes au groupe contigu de $2k$ personnes juste décalé d'une personne, le nombre de filles ne change pas beaucoup. Autrement dit, les valeurs de $N(n, k)$ et $N(n+1, k)$ doivent être proches. En fait, on voit aisément que
$$N(n+1, k) - N(n, k) = -a_n + 2a_{n+k} - a_{n+2k}.$$ Cette valeur est toujours dans l'intervalle $[-2, 2]$. Pour $k$ fixé, on connaît donc assez bien comment $N(n, k)$ varie lorsque $n$ varie. On aimerait donc analyser la suite (qui forme un cycle)
$$N(1, k), \quad N(2, k), \quad \ldots, \quad N(1000, k).$$ Une remarque intéressante est que la somme de ces $1000$ nombres est nulle ! En effet, chaque $a_i$ apparaît $k$ fois positivement et $k$ fois négativement dans ces termes. On a donc un cycle de $1000$ nombres dont la somme vaut $0$ et tel que $N(n+1, k) - N(n, k) \in [-2, 2]$ pour tout $n$. On fixe maintenant $k = 100$ et on en déduit, les termes ne pouvant tous être du même signe, qu'il existe un certain $n_0$ tel que
$$N(n_0, 100) = 1 \quad \text{et} \quad N(n_0+1, 100) = -1.$$ Rappelons que nous cherchons une absurdité, c'est-à-dire certainement des valeurs de $n$ et $k$ telles que $N(n, k) = 0$. Nous en sommes proches puisque nous avons trouvé $-1$ et $1$. Examinons ce que ces valeurs représentent. Au vu de la relation exhibée plus haut, elles impliquent $a_{n_0} = a_{n_0 + 200} = 1$ et $a_{n_0 + 100} = 0$. Autrement dit, la situation est la suivante :
$$1, a_{n_0+1}, \ldots, a_{n_0+99}, 0, a_{n_0+101}, \ldots, a_{n_0+199}, 1$$ avec $a_{n_0+1} + \ldots + a_{n_0+99} = a_{n_0+101} + \ldots + a_{n_0+199}$. Nous n'avons jusqu'ici utilisé que la valeur $k = 100$, mais rappelons-nous qu'elle peut aller jusque $300$.
Nous avons donné $201$ étudiants ci-dessus, et en considérant ceux-ci et le suivant, on voit que ce suivant doit être une fille pour avoir $N(n_0, 101) \neq 0$. Similairement, l'élève précédant ces $201$ étudiants doit être une fille, d'où on a
$$1, 1, a_{n_0+1}, \ldots, a_{n_0+99}, 0, a_{n_0+101}, \ldots, a_{n_0+199}, 1, 1.$$ On peut alors utiliser $k = 102$ pour trouver que les deux autres étudiants aux extrémités sont également des filles, et ainsi de suite jusque $k = 300$ ce qui nous donne finalement
$$\underbrace{1, \ldots, 1}_{200 \text{ fois}}, 1, a_{n_0+1}, \ldots, a_{n_0+99}, 0, a_{n_0+101}, \ldots, a_{n_0+199}, 1, \underbrace{1, \ldots, 1}_{200 \text{ fois}}.$$ On a donc trouvé $200$ filles consécutives, c'est-à-dire un bloc de $200$ étudiants dont la première moitié contient autant de filles que la deuxième : c'est une absurdité et cela termine le problème.