Théorie > Combinatoire > Dénombrement (suite)
Prérequis
Résumé
Nous avons vu précédemment comment dénombrer des possibilités à l'aide des formules de permutations, combinaisons et arrangements. Il n'est pas toujours possible d'appliquer ces formules directement, et l'objectif de ce chapitre est de présenter différentes méthodes permettant de résoudre certaines situations plus complexes.
Ce chapitre a été écrit par N. Radu et mis en ligne le 8 décembre 2014.
1. Comptage direct
Beaucoup de problèmes de combinatoire consistent à dénombrer les différentes possibilités d'un événement. Par exemple, on rencontre souvent des problèmes du type du problème suivant.
Face à un tel problème, l'envie la plus naturelle est de vouloir utiliser les formules donnant le nombre de permutations, d'arrangements ou de combinaisons. Il faut alors trouver la façon la plus simple de dénombrer les possibilités. Il est pour cela primordial que la situation soit bien claire et il faut à tout prix tâcher de compter les possibilités de manière logique et ordonnée. Nous donnons ci-dessous trois façons de procéder pour résoudre ce problème.
La méthode précédente ne fonctionnera cependant pas toujours. Il se peut en effet que le nombre de possibilités lors du placement d'une personne dépende des précédents placements : il n'est alors pas possible de procéder de cette manière. Il est donc bon de réussir à voir les choses autrement.
On peut également, au lieu d'effectuer des placements un par un, essayer de directement appliquer les formules de dénombrement pour évaluer le nombre de configurations possibles.
Problème
Quel est le nombre de manières d'asseoir $n$ couples (homme/femme) autour d'une table ronde de $2n$ places (numérotées), les hommes et les femmes devant être alternés ?
Face à un tel problème, l'envie la plus naturelle est de vouloir utiliser les formules donnant le nombre de permutations, d'arrangements ou de combinaisons. Il faut alors trouver la façon la plus simple de dénombrer les possibilités. Il est pour cela primordial que la situation soit bien claire et il faut à tout prix tâcher de compter les possibilités de manière logique et ordonnée. Nous donnons ci-dessous trois façons de procéder pour résoudre ce problème.
Solution 1
La manière la plus intuitive pour compter le nombre de façons de placer des gens autour d'une table est peut-être d'essayer de placer les convives un à un et d'évaluer le nombre de choix possibles à chaque placement. Il est tout de même préférable de se simplifier le comptage et donc de placer les personnes dans un ordre logique. On peut donc par exemple placer toutes les femmes et puis seulement tous les hommes, ou encore placer les couples un à un (c'est-à-dire alterner le placement d'un homme avec le placement d'une femme). Procédons de cette dernière manière. Pour le premier couple, on a bien sûr $2n$ places possibles pour l'homme. Puisqu'il faut alterner les hommes et les femmes, il reste alors $n$ places disponibles pour la femme. Pour le deuxième couple, on a $(n-1)$ choix restants pour l'homme et, de même, $(n-1)$ choix pour la femme. On continue ainsi de suite jusqu'au dernier couple, où il n'y a plus qu'une place disponible pour l'homme ainsi qu'une place pour la femme. On voit bien sûr que cette méthode de placement fonctionnera toujours, en ce sens que le placement final sera alterné et que l'on peut atteindre tous les placements possibles. Il ne reste alors plus qu'à multiplier tous les choix que nous avons eu pour obtenir le nombre total de possibilités :
$$2n \cdot n \cdot (n-1) \cdot (n-1) \cdot (n-2) \cdot (n-2) \cdot \ldots \cdot 2 \cdot 2 \cdot 1 \cdot 1.$$ Il suffit alors de réordonner les termes différemment pour obtenir la formule finale
$$2 (n!)^2.$$
$$2n \cdot n \cdot (n-1) \cdot (n-1) \cdot (n-2) \cdot (n-2) \cdot \ldots \cdot 2 \cdot 2 \cdot 1 \cdot 1.$$ Il suffit alors de réordonner les termes différemment pour obtenir la formule finale
$$2 (n!)^2.$$
La méthode précédente ne fonctionnera cependant pas toujours. Il se peut en effet que le nombre de possibilités lors du placement d'une personne dépende des précédents placements : il n'est alors pas possible de procéder de cette manière. Il est donc bon de réussir à voir les choses autrement.
Solution 2
Au lieu de placer les convives un à un, on peut par exemple plutôt considérer les sièges un à un et décider pour chacun qui y placer. Si nous considérons les sièges dans l'ordre, alors il y aura $2n$ possibilités pour le premier siège (puisque quiconque peut s'y placer), puis $n$ pour le deuxième (il faut placer quelqu'un du sexe opposé au premier), puis $(n-1)$ pour le troisième,... On obtient de cette manière exactement les mêmes termes que dans la première solution, ce qui donne évidemment la même réponse finale.
On peut également, au lieu d'effectuer des placements un par un, essayer de directement appliquer les formules de dénombrement pour évaluer le nombre de configurations possibles.
Solution 3
Si on numérote les places de $1$ à $2n$, on a tout d'abord deux possibilités : mettre les femmes sur les places paires ou sur les places impaires. Quitte à multiplier le résultat par $2$ à la fin, on peut décider que les femmes seront placées sur les places paires. Alors, le nombre de façons de disposer les $n$ femmes sur les $n$ places qui leur sont accordées est simplement le nombre de permutations de $n$ objets (ici les femmes, quoiqu'il ne faut pas considérer les femmes comme des objets :-)), c'est-à-dire $n!$. De la même façon, il y a $n!$ manières de permuter les hommes, et on a donc au final un nombre de possibilité égal à
$$2(n!)^2.$$
$$2(n!)^2.$$
Passage au complémentaire
Parfois, un comptage direct n'est pas possible, mais une simple transformation du problème permet de le résoudre : passer au problème complémentaire. Par exemple, face au problème suivant :Problème
Quel est le nombre de manières d'asseoir $n$ couples (homme/femme) autour d'une table ronde de $2n$ places (numérotées) de sorte qu'il y ait au moins deux personnes du même sexe l'une à côté de l'autre ?
Solution
Il ne semble pas faisable d'effectuer un comptage comme dans l'exemple précédent. Une idée simple est alors de vouloir compter les manières de s'asseoir qui ne respectent pas ces conditions. On se rend vite compte que cela n'arrive que si les hommes et les femmes sont alternés : on est donc ramenés au problème précédent ! Le nombre recherché est donc le nombre total de manières de s'asseoir, qui n'est autre que $(2n)!$ (le nombre de permutations de $2n$ objets), moins le résultat précédent $2(n!)^2$, c'est-à-dire
$$(2n)! - 2(n!)^2.$$
$$(2n)! - 2(n!)^2.$$
2. Bijection
Il n'est cependant pas toujours possible de compter directement le nombre de possibilités. Considérons l'exemple suivant.
Dans l'idée de procéder comme dans la section précédente, on peut essayer de choisir les $k$ éléments un par un. On a, pour le premier élément, $n$ choix possibles. Disons que l'on a choisi $x_1$. Lors du choix du deuxième élément $x_2$, on ne peut alors plus prendre $x_1$, mais on ne peut pas non plus prendre $x_1 - 1$ ou $x_1+1$. Si $x_1 = 1$, alors il y a deux valeurs interdites ($1$ et $2$), tout comme si $x_1 = n$ ($n$ et $n-1$), mais il y a trois valeurs interdites lorsque $x_1 \in \{2, 3, \ldots, n-1\}$. Il faut donc pour continuer distinguer le cas où $x_1$ vaut $1$ ou $n$ des autres cas. Mais maintenant, lors du choix du troisième élément, le nombre de valeurs interdites dépend de $x_1$ et de $x_2$, et le nombre de cas ne fait que grandir ! Il n'est donc pas possible de trouver une solution avec cette méthode. (Notons que si elle avait abouti, il aurait fallu diviser le résultat par $k!$ à la fin puisque l'on aurait tenu compte de l'ordre de nos choix.)
On peut alors décider d'effectuer un comptage plus astucieux, en choisissant nos éléments dans l'ordre croissant. On a alors à nouveau $n$ possibilités pour $x_1$. Pour $x_2$, il nous faut choisir une valeur supérieure ou égale à $x_1+2$ : il y a donc $n-x_1-1$ possibilités. Ce nombre dépendant de $x_1$, il semble encore une fois compliqué de continuer dans cette voie. En effet, le nombre de possibilités pour $x_3$ dépendra à son tour des valeurs de $x_1$ et $x_2$ et ainsi de suite, et cette dépendance ne peut pas être gérée facilement.
Ce problème ne semble pas aussi simple à résoudre que l'exemple précédent. Dans une telle situation, une technique est d'essayer de se ramener à un problème plus simple. Notre exemple ressemble fort au nombre de combinaisons de $k$ objets parmi $n$, il y a uniquement la contrainte que l'on ne peut pas prendre des nombres consécutifs. Ne serait-il pas possible de passer d'une situation à l'autre ?
Problème
Quel est le nombre de sous-ensembles à $k$ éléments de $\{1, 2, \ldots, n\}$ ne contenant pas d'entiers consécutifs ?
Dans l'idée de procéder comme dans la section précédente, on peut essayer de choisir les $k$ éléments un par un. On a, pour le premier élément, $n$ choix possibles. Disons que l'on a choisi $x_1$. Lors du choix du deuxième élément $x_2$, on ne peut alors plus prendre $x_1$, mais on ne peut pas non plus prendre $x_1 - 1$ ou $x_1+1$. Si $x_1 = 1$, alors il y a deux valeurs interdites ($1$ et $2$), tout comme si $x_1 = n$ ($n$ et $n-1$), mais il y a trois valeurs interdites lorsque $x_1 \in \{2, 3, \ldots, n-1\}$. Il faut donc pour continuer distinguer le cas où $x_1$ vaut $1$ ou $n$ des autres cas. Mais maintenant, lors du choix du troisième élément, le nombre de valeurs interdites dépend de $x_1$ et de $x_2$, et le nombre de cas ne fait que grandir ! Il n'est donc pas possible de trouver une solution avec cette méthode. (Notons que si elle avait abouti, il aurait fallu diviser le résultat par $k!$ à la fin puisque l'on aurait tenu compte de l'ordre de nos choix.)
On peut alors décider d'effectuer un comptage plus astucieux, en choisissant nos éléments dans l'ordre croissant. On a alors à nouveau $n$ possibilités pour $x_1$. Pour $x_2$, il nous faut choisir une valeur supérieure ou égale à $x_1+2$ : il y a donc $n-x_1-1$ possibilités. Ce nombre dépendant de $x_1$, il semble encore une fois compliqué de continuer dans cette voie. En effet, le nombre de possibilités pour $x_3$ dépendra à son tour des valeurs de $x_1$ et $x_2$ et ainsi de suite, et cette dépendance ne peut pas être gérée facilement.
Ce problème ne semble pas aussi simple à résoudre que l'exemple précédent. Dans une telle situation, une technique est d'essayer de se ramener à un problème plus simple. Notre exemple ressemble fort au nombre de combinaisons de $k$ objets parmi $n$, il y a uniquement la contrainte que l'on ne peut pas prendre des nombres consécutifs. Ne serait-il pas possible de passer d'une situation à l'autre ?
Solution
Lorsque l'on choisit simplement $k$ éléments $\{y_1, y_2, \ldots, y_k\}$ (disons avec $y_1 < y_2 < \ldots < y_k$) dans $\{1, 2, \ldots, n\}$, l'unique problème est qu'il se peut que certains éléments soient consécutifs. Une idée serait donc, une fois que l'on a choisi $\{y_1, y_2, \ldots, y_k\}$, de modifier ces choix pour être certain que les éléments ne soient pas consécutifs. Une façon simple de procéder est de remplacer $y_2$ par $y_2 + 1$ (de sorte que ce nouvel élément ne soit jamais consécutif à $y_1$), puis $y_3$ par $y_3+2$, et ainsi de suite jusque $y_k$ que l'on remplace par $y_k+k-1$. Évidemment le lecteur averti aura remarqué qu'il se peut maintenant que ces éléments dépassent $n$. On peut cependant éviter ce dépassement en imposant à nos $y_1, y_2, \ldots, y_k$ d'être inférieurs ou égaux à $n-k+1$ et non plus $n$. En résumé, il est possible d'associer à
$$\{y_1, y_2, \ldots, y_k\} \subseteq \{1, 2, \ldots, n-k+1\}$$ (avec $y_1 < y_2 < \ldots < y_k$) l'ensemble
$$\{x_1, x_2, \ldots, x_k\} = \{y_1, y_2+1, \ldots, y_k+k-1\} \subseteq \{1, 2, \ldots, n\}$$ (avec $x_1 < x_2 < \ldots < x_k$) , et ce nouvel ensemble ne contient pas d'entiers consécutifs ! Or, on se convainc facilement qu'avec cette méthode, nous allons atteindre tous les sous-ensembles à $k$ éléments de $\{1, 2, \ldots, n\}$ ne contenant pas d'entiers consécutifs. En effet, un tel sous-ensemble
$$\{x_1, x_2, \ldots, x_k\} \subseteq \{1, 2, \ldots, n\}$$ proviendra toujours du sous-ensemble
$$\{y_1, y_2, \ldots, y_n\} = \{x_1, x_2-1, \ldots, x_k-k+1\} \subseteq \{1, 2, \ldots, n-k+1\}.$$
Ce que nous venons de montrer, c'est qu'il existe une bijection entre les sous-ensembles à $k$ éléments de $\{1, 2, \ldots, n-k+1\}$ et les sous-ensembles à $k$ éléments de $\{1, 2, \ldots, n\}$ ne contenant pas d'entiers consécutifs. Une bijection entre deux ensembles $A$ et $B$ consiste en effet en une fonction associant à chaque élément de $A$ un élément de $B$, de sorte que l'on puisse, à partir d'un élément de $B$, retrouver l'élément de $A$ duquel il provient (on montre en fait qu'il existe une fonction inverse). Or, lorsque l'on a une telle bijection entre $A$ et $B$, les deux ensembles ont forcément le même cardinal (ils ont le même nombre d'éléments).
Dans notre situation, cela signifie que le nombre de sous-ensembles à $k$ éléments de $\{1, 2, \ldots, n-k+1\}$ est exactement égal au nombre de sous-ensembles à $k$ éléments de $\{1, 2, \ldots, n\}$ sans entiers consécutifs, c'est-à-dire la valeur que nous cherchons. Or, le nombre de sous-ensembles à $k$ éléments de $\{1, 2, \ldots, n-k+1\}$ est simplement le nombre de combinaisons de $k$ objets parmi $n-k+1$, ce qui est égal à $C^k_{n-k+1}$. Il s'agit donc de la réponse attendue.
$$\{y_1, y_2, \ldots, y_k\} \subseteq \{1, 2, \ldots, n-k+1\}$$ (avec $y_1 < y_2 < \ldots < y_k$) l'ensemble
$$\{x_1, x_2, \ldots, x_k\} = \{y_1, y_2+1, \ldots, y_k+k-1\} \subseteq \{1, 2, \ldots, n\}$$ (avec $x_1 < x_2 < \ldots < x_k$) , et ce nouvel ensemble ne contient pas d'entiers consécutifs ! Or, on se convainc facilement qu'avec cette méthode, nous allons atteindre tous les sous-ensembles à $k$ éléments de $\{1, 2, \ldots, n\}$ ne contenant pas d'entiers consécutifs. En effet, un tel sous-ensemble
$$\{x_1, x_2, \ldots, x_k\} \subseteq \{1, 2, \ldots, n\}$$ proviendra toujours du sous-ensemble
$$\{y_1, y_2, \ldots, y_n\} = \{x_1, x_2-1, \ldots, x_k-k+1\} \subseteq \{1, 2, \ldots, n-k+1\}.$$
Ce que nous venons de montrer, c'est qu'il existe une bijection entre les sous-ensembles à $k$ éléments de $\{1, 2, \ldots, n-k+1\}$ et les sous-ensembles à $k$ éléments de $\{1, 2, \ldots, n\}$ ne contenant pas d'entiers consécutifs. Une bijection entre deux ensembles $A$ et $B$ consiste en effet en une fonction associant à chaque élément de $A$ un élément de $B$, de sorte que l'on puisse, à partir d'un élément de $B$, retrouver l'élément de $A$ duquel il provient (on montre en fait qu'il existe une fonction inverse). Or, lorsque l'on a une telle bijection entre $A$ et $B$, les deux ensembles ont forcément le même cardinal (ils ont le même nombre d'éléments).
Dans notre situation, cela signifie que le nombre de sous-ensembles à $k$ éléments de $\{1, 2, \ldots, n-k+1\}$ est exactement égal au nombre de sous-ensembles à $k$ éléments de $\{1, 2, \ldots, n\}$ sans entiers consécutifs, c'est-à-dire la valeur que nous cherchons. Or, le nombre de sous-ensembles à $k$ éléments de $\{1, 2, \ldots, n-k+1\}$ est simplement le nombre de combinaisons de $k$ objets parmi $n-k+1$, ce qui est égal à $C^k_{n-k+1}$. Il s'agit donc de la réponse attendue.
3. Inclusion-exclusion
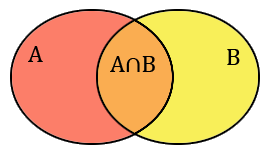
Le principe d'inclusion-exclusion est une formule permettant de calculer le nombre d'éléments dans une union d'ensembles à partir du nombre d'éléments dans leurs différentes intersections. L'exemple le plus simple consiste en deux ensembles $A$ et $B$. S'ils sont disjoints (ils n'ont aucun élément en commun), alors on a bien sûr $|A \cup B| = |A| + |B|$. Par contre, s'ils ont des éléments communs, alors en calculant cette somme $|A|+|B|$, on compte deux fois les éléments qui sont dans $A \cap B$ (c'est-à-dire dans $A$ et $B$ à la fois). Il faut donc retirer le nombre d'éléments communs aux deux ensembles, et on a la formule générale suivante :
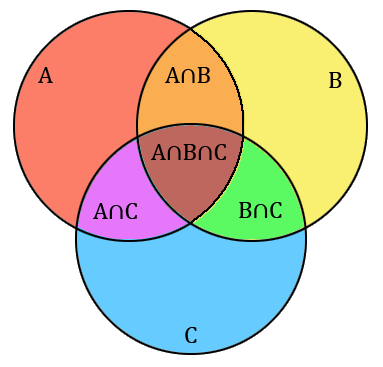
On peut faire le même raisonnement pour trois ensembles $A$, $B$ et $C$. On commence par calculer la somme $|A| + |B| + |C|$, mais encore une fois on a compté plus d'une fois les éléments se situant dans deux ensembles à la fois. On retranche donc $|A \cap B| + |B \cap C| + |C \cap A|$ du résultat. Mais si maintenant, on considère les éléments se situant dans les trois ensembles à la fois, alors on les a compté trois fois chacun lors de la première somme avant de les retrancher trois fois : on n'a donc au final pas compté ces éléments ! Il faut donc à nouveau compter les éléments de $A \cap B \cap C$, ce qui donne la formule suivante :
On comprend mieux le terme inclusion-exclusion, puisqu'on ajoute certains termes avant d'en retrancher d'autres, puis d'en rajouter à nouveau.
Ce raisonnement se généralise en fait à $n$ ensembles :
Cette formule peut sembler compliquée mais elle ne fait que généraliser les formules que nous avons vues pour $n = 2$ et $n= 3$. En effet, pour $k = 1$ on retrouve tous les ensembles seuls, pour $k = 2$, on a $(-1)^{2-1} = -1$ et on retire donc les cardinaux de toutes les intersections deux par deux, puis pour $k = 3$ on rajoute les intersections trois par trois, et ainsi de suite jusqu'à l'intersection de tous les ensembles.
L'erreur type est de se dire "Il y a $500$ nombres pairs, $333$ nombres divisibles par $3$ et $200$ nombres divisibles par $5$, donc la réponse est $500+333+200=1033$." Évidemment, on constate immédiatement que le raisonnement est erroné puisqu'on obtient une réponse supérieure à $1000$. Le problème est que nous avons compté plusieurs fois les nombres multiples de $6$, de $10$ ou de $15$ : il s'agit exactement du principe de l'inclusion-exclusion.
Il existe aussi des exemples du même type que ceux que nous avons rencontrés jusqu'à présent, comme le suivant.
Principe d'inclusion-exclusion (pour $2$ ensembles)
$$|A \cup B| = |A| + |B| - |A \cap B|.$$

On peut faire le même raisonnement pour trois ensembles $A$, $B$ et $C$. On commence par calculer la somme $|A| + |B| + |C|$, mais encore une fois on a compté plus d'une fois les éléments se situant dans deux ensembles à la fois. On retranche donc $|A \cap B| + |B \cap C| + |C \cap A|$ du résultat. Mais si maintenant, on considère les éléments se situant dans les trois ensembles à la fois, alors on les a compté trois fois chacun lors de la première somme avant de les retrancher trois fois : on n'a donc au final pas compté ces éléments ! Il faut donc à nouveau compter les éléments de $A \cap B \cap C$, ce qui donne la formule suivante :
Principe d'inclusion-exclusion (pour $3$ ensembles)
$$|A \cup B \cup C| = |A| + |B| + |C| - |A\cap B| - |B \cap C| - |C \cap A| + |A \cap B \cap C|.$$
On comprend mieux le terme inclusion-exclusion, puisqu'on ajoute certains termes avant d'en retrancher d'autres, puis d'en rajouter à nouveau.

Ce raisonnement se généralise en fait à $n$ ensembles :
Principe d'inclusion-exclusion (pour $n$ ensembles)
Soient $A_1, \ldots, A_n$ des ensembles. On a
$$|A_1 \cup \ldots \cup A_n| = \sum_{k=1}^n \left( (-1)^{k-1} \sum_{1\leq i_1 < \ \ldots \ < i_k \leq n} |A_{i_1} \cap \ldots \cap A_{i_k}| \right).$$
$$|A_1 \cup \ldots \cup A_n| = \sum_{k=1}^n \left( (-1)^{k-1} \sum_{1\leq i_1 < \ \ldots \ < i_k \leq n} |A_{i_1} \cap \ldots \cap A_{i_k}| \right).$$
Cette formule peut sembler compliquée mais elle ne fait que généraliser les formules que nous avons vues pour $n = 2$ et $n= 3$. En effet, pour $k = 1$ on retrouve tous les ensembles seuls, pour $k = 2$, on a $(-1)^{2-1} = -1$ et on retire donc les cardinaux de toutes les intersections deux par deux, puis pour $k = 3$ on rajoute les intersections trois par trois, et ainsi de suite jusqu'à l'intersection de tous les ensembles.
Application en combinatoire
Voici un exemple assez connu où le principe d'inclusion-exclusion se révèle très utile :Problème
Combien y a-t-il de nombres compris entre $1$ et $1000$ divisibles par $2$, par $3$ ou par $5$ ?
L'erreur type est de se dire "Il y a $500$ nombres pairs, $333$ nombres divisibles par $3$ et $200$ nombres divisibles par $5$, donc la réponse est $500+333+200=1033$." Évidemment, on constate immédiatement que le raisonnement est erroné puisqu'on obtient une réponse supérieure à $1000$. Le problème est que nous avons compté plusieurs fois les nombres multiples de $6$, de $10$ ou de $15$ : il s'agit exactement du principe de l'inclusion-exclusion.
Solution
Notons $A$ l'ensemble des nombres (entre $1$ et $1000$) pairs, $B$ l'ensemble des nombres multiples de $3$ et $C$ l'ensemble des nombres multiples de $5$. Nous cherchons alors le cardinal de $A \cup B \cup C$, et le principe d'inclusion-exclusion s'applique :
$$|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |B \cap C| - |C \cap A| + |A \cap B \cap C|.$$ Or, on a $|A| = 500$, $|B| = 333$, $|C| = 200$, $|A \cap B| = 166$ (car $A \cap B$ est l'ensemble des nombres multiples de $6$), $|B \cap C| = 66$, $|C \cap A| = 100$ et $|A \cap B \cap C| = 33$, d'où au final
$$|A \cup B \cup C| = 500+333+200-166-66-100+33=\boxed{734}.$$
$$|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |B \cap C| - |C \cap A| + |A \cap B \cap C|.$$ Or, on a $|A| = 500$, $|B| = 333$, $|C| = 200$, $|A \cap B| = 166$ (car $A \cap B$ est l'ensemble des nombres multiples de $6$), $|B \cap C| = 66$, $|C \cap A| = 100$ et $|A \cap B \cap C| = 33$, d'où au final
$$|A \cup B \cup C| = 500+333+200-166-66-100+33=\boxed{734}.$$
Il existe aussi des exemples du même type que ceux que nous avons rencontrés jusqu'à présent, comme le suivant.
Problème
Je possède $8$ photos différentes de mes vacances, et je désire les distribuer à mes $5$ amis. Pour que tout le monde soit content, chaque ami doit recevoir au moins une photo. De combien de manières puis-je effectuer ma distribution ?
Solution
S'il n'y avait pas la condition comme quoi chaque ami doit recevoir au moins une photo, on pourrait simplement considérer les photos une à une et décider pour chacune à qui on la donne : on aurait donc $5^8$ possibilités. En fait, on peut le voir comme un arrangement avec répétitions de $8$ objets parmi $5$. Le minimum d'une photo par personne nous empêche cependant de procéder de la sorte, et il n'est pas évident de voir comment on pourrait effectuer un comptage direct. Une idée déjà suggérée dans ce chapitre est alors de passer au complémentaire, c'est-à-dire de compter le nombre de façons de distribuer les photos de sorte qu'au moins un ami ne recoive aucune photo. Cela nous fait penser au principe d'inclusion exclusion, puisqu'en notant
$$A_i = \{\text{distributions où l'ami numéro $i$ ne reçoit pas de photo}\},$$ on cherche le cardinal de $A_1 \cup \ldots \cup A_5$. Pour que le principe d'inclusion-exclusion soit utile, il faut qu'il soit facile d'évaluer le cardinal d'une intersection de $A_i$. Mais cela est effectivement aisé ! En effet, le cardinal d'une intersection $A_{i_1} \cap \ldots \cap A_{i_k}$ (avec $k$ ensembles différents) représente le nombre de façons de distribuer $8$ photos à $5$ amis sans en donner aux amis numéro $i_1, \ldots, i_k$. Cela revient à distribuer $8$ photos à $5-k$ amis, et le cardinal vaut donc $(5-k)^8$. Le principe d'inclusion-exclusion donne donc :
$$\begin{align}
|A_1 \cup \ldots \cup A_5| & = \sum_{k=1}^5 \left( (-1)^{k-1} \sum_{1\leq i_1 < \ \ldots \ < i_k \leq 5} |A_{i_1} \cap \ldots \cap A_{i_k}| \right) \\
& = \sum_{k=1}^5 \left( (-1)^{k-1} \sum_{1\leq i_1 < \ \ldots \ < i_k \leq 5} (5-k)^8 \right)
\end{align}$$ Pour $k$ fixé, les termes de la somme intérieure sont tous identiques (égaux à $(5-k)^8$, et il reste donc juste à évaluer combien il y a de termes dans cette somme. Le nombre de termes est simplement égal au nombre de façons de choisir les indices $i_1, \ldots, i_k$ dans $\{1, \ldots, 5\}$, c'est-à-dire égal à $C^k_5$. On a donc
$$\begin{align}
|A_1 \cup \ldots \cup A_5| & = \sum_{k=1}^5 \left( (-1)^{k-1} \cdot C^k_5 \cdot(5-k)^8 \right) \\[2mm]
&= C^1_5 \cdot 4^8 - C^2_5 \cdot 3^8 + C^3_5 \cdot 2^8 - C^4_5 \cdot 1^8 + C^5_5 \cdot 0^8 \\[2mm]
&= 5\cdot 65536 - 10 \cdot 6561 + 10 \cdot 256 - 5 \cdot 1\\[2mm]
&= 264625
\end{align}$$ La réponse au problème initial est donc $5^8 - 264625 = \boxed{126000}$.
$$A_i = \{\text{distributions où l'ami numéro $i$ ne reçoit pas de photo}\},$$ on cherche le cardinal de $A_1 \cup \ldots \cup A_5$. Pour que le principe d'inclusion-exclusion soit utile, il faut qu'il soit facile d'évaluer le cardinal d'une intersection de $A_i$. Mais cela est effectivement aisé ! En effet, le cardinal d'une intersection $A_{i_1} \cap \ldots \cap A_{i_k}$ (avec $k$ ensembles différents) représente le nombre de façons de distribuer $8$ photos à $5$ amis sans en donner aux amis numéro $i_1, \ldots, i_k$. Cela revient à distribuer $8$ photos à $5-k$ amis, et le cardinal vaut donc $(5-k)^8$. Le principe d'inclusion-exclusion donne donc :
$$\begin{align}
|A_1 \cup \ldots \cup A_5| & = \sum_{k=1}^5 \left( (-1)^{k-1} \sum_{1\leq i_1 < \ \ldots \ < i_k \leq 5} |A_{i_1} \cap \ldots \cap A_{i_k}| \right) \\
& = \sum_{k=1}^5 \left( (-1)^{k-1} \sum_{1\leq i_1 < \ \ldots \ < i_k \leq 5} (5-k)^8 \right)
\end{align}$$ Pour $k$ fixé, les termes de la somme intérieure sont tous identiques (égaux à $(5-k)^8$, et il reste donc juste à évaluer combien il y a de termes dans cette somme. Le nombre de termes est simplement égal au nombre de façons de choisir les indices $i_1, \ldots, i_k$ dans $\{1, \ldots, 5\}$, c'est-à-dire égal à $C^k_5$. On a donc
$$\begin{align}
|A_1 \cup \ldots \cup A_5| & = \sum_{k=1}^5 \left( (-1)^{k-1} \cdot C^k_5 \cdot(5-k)^8 \right) \\[2mm]
&= C^1_5 \cdot 4^8 - C^2_5 \cdot 3^8 + C^3_5 \cdot 2^8 - C^4_5 \cdot 1^8 + C^5_5 \cdot 0^8 \\[2mm]
&= 5\cdot 65536 - 10 \cdot 6561 + 10 \cdot 256 - 5 \cdot 1\\[2mm]
&= 264625
\end{align}$$ La réponse au problème initial est donc $5^8 - 264625 = \boxed{126000}$.
4. Récurrence
Une autre méthode pour résoudre des problèmes de dénombrement est la récurrence. Pour illustrer cela, considérons à nouveau l'exemple suivant.
Nous avons déjà résolu ce problème en le ramenant à un problème plus simple, via une bijection. Il est cependant aussi possible de s'en sortir sans remarquer qu'une telle bijection existe, en procédant par récurrence.
La principale difficulté de cette méthode est de trouver la relation de récurrence que la réponse vérifie. En effet, deviner la réponse et montrer par récurrence qu'elle est correcte constitue généralement une formalité (pourvu que l'on soit familier avec les coefficients binomiaux).
Problème
Quel est le nombre de sous-ensembles à $k$ éléments de $\{1, 2, \ldots, n\}$ ne contenant pas d'entiers consécutifs ?
Nous avons déjà résolu ce problème en le ramenant à un problème plus simple, via une bijection. Il est cependant aussi possible de s'en sortir sans remarquer qu'une telle bijection existe, en procédant par récurrence.
Solution via une récurrence
Il faut tout d'abord trouver une relation de récurrence que le problème vérifie. On peut pour cela noter $N(n,k)$ la réponse attendue, c'est-à-dire le nombre de sous-ensembles à $k$ éléments de $\{1,2, \ldots, n\}$ sans entiers consécutifs, et chercher s'il est possible de trouver une formule pour $N(n, k)$ à partir de valeurs inférieures, comme par exemple $N(n-1,k)$ ou $N(n, k-1)$.
Cherchons une telle relation. On considère pour cela un sous-ensemble $E$ à $k$ éléments de $\{1, 2, \ldots, n\}$ sans entiers consécutifs et on cherche à se ramener à une situation similaire avec des variables plus petites. Si $E$ ne contient pas $n$, alors il s'agit également d'un sous-ensemble de $\{1, 2, \ldots, n-1\}$ et est donc pris en compte lorsqu'on calcule $N(n-1, k)$. En fait, on a clairement une bijection entre les sous-ensembles pris en compte dans $N(n, k)$ ne contenant pas $n$ et les sous-ensembles pris en compte dans $N(n-1, k)$.
Il reste à considérer le cas où $E$ contient $n$. Dans ce cas, $E \setminus \{n\}$ est un sous-ensemble à $(k-1)$ éléments de $\{1, 2, \ldots, n-1\}$. En fait, puisque $E$ contient $n$ et ne contient pas deux éléments consécutifs, il ne peut pas contenir $(n-1)$. L'ensemble $E \setminus \{n\}$ est donc même contenu dans $\{1, 2, \ldots, n-2\}$, et il est donc pris en compte dans $N(n-2,k-1)$. Réciproquement, en présence d'un sous-ensemble à $(k-1)$ éléments de $\{1, 2, \ldots, n-2\}$ sans entiers consécutifs, on peut bien sûr lui rajouter l'élément $n$ et obtenir un ensemble pris en compte dans $N(n,k)$. On a donc une bijection entre les sous-ensembles pris en compte dans $N(n, k)$ contenant $n$ et les sous-ensembles pris en compte dans $N(n-2, k-1)$.
De ces constatations, on déduit l'égalité
$$N(n, k) = N(n-1, k) + N(n-2,k-1).$$
L'étape suivante dans la résolution du problème est alors de "deviner" sa réponse. Cela se fait généralement en la calculant pour les petites valeurs des variables. Dans notre situation, on peut par exemple remarquer que :
Comme notre relation permet de remplacer $n$ par $(n-1)$ et $(n-2)$, la récurrence la plus facile à exécuter est une récurrence sur $n$. On voit facilement que la formule que nous avons devinée est bien vérifiée pour $n = 1$ et $n = 2$, ce qui constitue le cas de base de notre récurrence. Supposons à présent que la formule est correcte pour $(n-2)$ et $(n-1)$ et montrons-la pour $n$. Vu notre relation, il suffit de prouver que
$$C^k_{n+1-k} = C^k_{n-k} + C^{k-1}_{n-k}.$$ Mais il s'agit là de la relation de Pascal (où $n$ a été remplacé par $(n+1-k)$) ! Nous venons donc de montrer que
$$N(n, k) = C^k_{n-k+1}.$$
Cherchons une telle relation. On considère pour cela un sous-ensemble $E$ à $k$ éléments de $\{1, 2, \ldots, n\}$ sans entiers consécutifs et on cherche à se ramener à une situation similaire avec des variables plus petites. Si $E$ ne contient pas $n$, alors il s'agit également d'un sous-ensemble de $\{1, 2, \ldots, n-1\}$ et est donc pris en compte lorsqu'on calcule $N(n-1, k)$. En fait, on a clairement une bijection entre les sous-ensembles pris en compte dans $N(n, k)$ ne contenant pas $n$ et les sous-ensembles pris en compte dans $N(n-1, k)$.
Il reste à considérer le cas où $E$ contient $n$. Dans ce cas, $E \setminus \{n\}$ est un sous-ensemble à $(k-1)$ éléments de $\{1, 2, \ldots, n-1\}$. En fait, puisque $E$ contient $n$ et ne contient pas deux éléments consécutifs, il ne peut pas contenir $(n-1)$. L'ensemble $E \setminus \{n\}$ est donc même contenu dans $\{1, 2, \ldots, n-2\}$, et il est donc pris en compte dans $N(n-2,k-1)$. Réciproquement, en présence d'un sous-ensemble à $(k-1)$ éléments de $\{1, 2, \ldots, n-2\}$ sans entiers consécutifs, on peut bien sûr lui rajouter l'élément $n$ et obtenir un ensemble pris en compte dans $N(n,k)$. On a donc une bijection entre les sous-ensembles pris en compte dans $N(n, k)$ contenant $n$ et les sous-ensembles pris en compte dans $N(n-2, k-1)$.
De ces constatations, on déduit l'égalité
$$N(n, k) = N(n-1, k) + N(n-2,k-1).$$
L'étape suivante dans la résolution du problème est alors de "deviner" sa réponse. Cela se fait généralement en la calculant pour les petites valeurs des variables. Dans notre situation, on peut par exemple remarquer que :
- $N(n, 0) = 1$ pour tout $n$, car il n'y a qu'une seule manière de ne choisir aucun nombre.
- $N(n, 1) = n$ pour tout $n$, car il y a $n$ façons de choisir un élément de $\{1, 2, \ldots, n\}$.
- $N(n, 2) = \frac{(n-2)(n-1)}{2}$. En effet, si on choisit $1$ pour le plus petit des deux éléments, alors on a $(n-2)$ choix pour le second; si on choisit $2$, alors on a $(n-3)$ choix pour le second; et ainsi de suite. Au total, il y a donc $(n-2)+(n-3)+\ldots+2+1 = \frac{(n-2)(n-1)}{2}$ sous-ensembles vérifiant les conditions.
Comme notre relation permet de remplacer $n$ par $(n-1)$ et $(n-2)$, la récurrence la plus facile à exécuter est une récurrence sur $n$. On voit facilement que la formule que nous avons devinée est bien vérifiée pour $n = 1$ et $n = 2$, ce qui constitue le cas de base de notre récurrence. Supposons à présent que la formule est correcte pour $(n-2)$ et $(n-1)$ et montrons-la pour $n$. Vu notre relation, il suffit de prouver que
$$C^k_{n+1-k} = C^k_{n-k} + C^{k-1}_{n-k}.$$ Mais il s'agit là de la relation de Pascal (où $n$ a été remplacé par $(n+1-k)$) ! Nous venons donc de montrer que
$$N(n, k) = C^k_{n-k+1}.$$
La principale difficulté de cette méthode est de trouver la relation de récurrence que la réponse vérifie. En effet, deviner la réponse et montrer par récurrence qu'elle est correcte constitue généralement une formalité (pourvu que l'on soit familier avec les coefficients binomiaux).
Remarque
Cette méthode semble ne fonctionner que lorsqu'une ou plusieurs variables comme $n$ et $k$ sont présentes dans le problème, mais il n'y a en fait pas réellement de telle restriction. En effet, si un problème de dénombrement ne comporte pas de variables, alors il contient généralement à la place un ou plusieurs nombres plutôt grands (de sorte que le problème ne soit pas résoluble en testant les cas un par un). Il ne faut alors pas hésiter à remplacer ce ou ces nombres par des variables, et à résoudre le problème en toute généralité. En plus de permettre une éventuelle récurrence, une telle démarche permet de donner des plus petites valeurs aux variables introduites et de parfois deviner la forme générale de la réponse (et a fortiori la réponse pour les grandes valeurs du problème). Il reste évidemment à prouver que cette réponse est correcte.