Théorie > Géométrie > Cercles d'Apollonius
Prérequis
Résumé
Étant donné un triangle, on peut définir trois cercles particuliers associés à celui-ci, appelés cercles d'Apollonius. Ceux-ci ont des propriétés intéressantes et sont par exemple étroitement liés à la notion de triangle podaire. Connaître l'existence de ces cercles ainsi que leurs propriétés peut être d'une grande aide dans la résolution de problèmes, qu'ils soient basiques ou avancés.
Ce chapitre a été écrit par N. Radu et mis en ligne le 7 mars 2015.
1. Définition
Étant donné un triangle $ABC$, on peut tracer trois cercles particuliers. On définit en effet le $A$-cercle d'Apollonius comme étant le lieu des points $X$ tels que
$$\displaystyle \frac{|XB|}{|XC|} = \frac{|AB|}{|AC|}.$$ On définit le $B$-cercle d'Apollonius et le $C$-cercle d'Apollonius de la même manière.
Il n'est a priori pas évident que ces lieux sont effectivement des cercles, mais il s'agit en fait d'un simple exercice de géométrie analytique. Cela dit, ces cercles se dégénèrent parfois en une droite. Plus précisément, le $A$-cercle d'Apollonius prend la forme d'une droite si et seulement si $|AB| = |AC|$ et il s'agit simplement dans ce cas de la médiatrice de $[BC]$.
Ces cercles sont intéressants de par leurs propriétés. Intéressons-nous de plus près au $A$-cercle d'Apollonius. Par définition, on voit déjà directement qu'il passe par le point $A$. D'autre part, le théorème de la bissectrice nous apprend également que ce cercle passe par $A'$, l'intersection de la bissectrice intérieure de $A$ avec $BC$, et $A''$, l'intersection de la bissectrice extérieure de $A$ avec $BC$. Puisque $\widehat{A'AA''} = 90^\circ$, il s'agit donc simplement du cercle de diamètre $[A'A'']$. Ce cercle est représenté à droite sur la figure suivante.
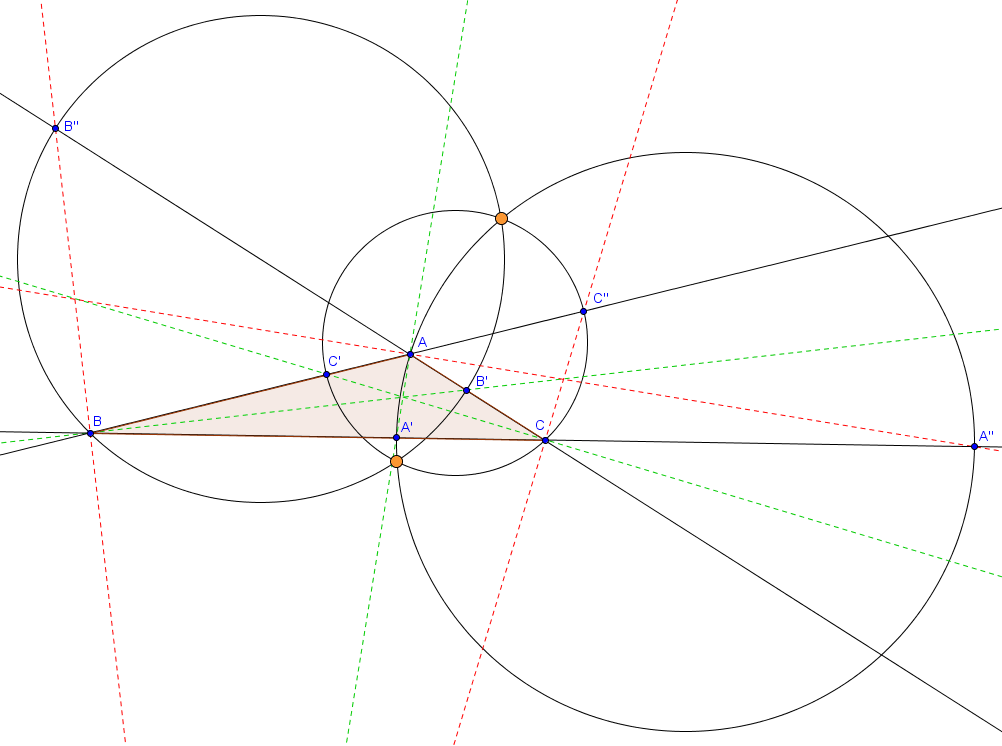
Les trois cercles d'Apollonius associés à un triangle.
Comme on peut le voir sur cette figure, les trois cercles semblent se couper en exactement deux points. On peut en fait démontrer ce résultat sans trop de peine.
Dans le cas particulier où le triangle est équilatéral, les trois "cercles" sont les trois médiatrices du triangle et ils se rencontrent donc en un unique point.
$$\displaystyle \frac{|XB|}{|XC|} = \frac{|AB|}{|AC|}.$$ On définit le $B$-cercle d'Apollonius et le $C$-cercle d'Apollonius de la même manière.
Il n'est a priori pas évident que ces lieux sont effectivement des cercles, mais il s'agit en fait d'un simple exercice de géométrie analytique. Cela dit, ces cercles se dégénèrent parfois en une droite. Plus précisément, le $A$-cercle d'Apollonius prend la forme d'une droite si et seulement si $|AB| = |AC|$ et il s'agit simplement dans ce cas de la médiatrice de $[BC]$.
Ces cercles sont intéressants de par leurs propriétés. Intéressons-nous de plus près au $A$-cercle d'Apollonius. Par définition, on voit déjà directement qu'il passe par le point $A$. D'autre part, le théorème de la bissectrice nous apprend également que ce cercle passe par $A'$, l'intersection de la bissectrice intérieure de $A$ avec $BC$, et $A''$, l'intersection de la bissectrice extérieure de $A$ avec $BC$. Puisque $\widehat{A'AA''} = 90^\circ$, il s'agit donc simplement du cercle de diamètre $[A'A'']$. Ce cercle est représenté à droite sur la figure suivante.

Les trois cercles d'Apollonius associés à un triangle.
Comme on peut le voir sur cette figure, les trois cercles semblent se couper en exactement deux points. On peut en fait démontrer ce résultat sans trop de peine.
Proposition (cercles d'Apollonius)
Les trois cercles d'Apollonius d'un triangle (non équilatéral) se rencontrent en exactement deux points.
Démonstration
Soit $ABC$ un triangle non équilatéral, disons avec $|AB| \neq |AC|$. Par définition, on a directement que si un point appartient à deux des cercles, alors il appartient au troisième. En effet, si
$$\displaystyle \frac{|XB|}{|XC|} = \frac{|AB|}{|AC|} \quad \text{ et } \quad \frac{|XA|}{|XB|} = \frac{|CA|}{|CB|},$$ alors il suffit de multiplier les deux égalités pour obtenir la troisième :
$$\displaystyle \frac{|XA|}{|XC|} = \frac{|BA|}{|BC|}.$$ Or, on se convainc facilement que les cercles ne sont pas tangents ni disjoints. En effet, comme $|AB| \neq |AC|$ le $A$-cercle d'Apollonius est bien un cercle. De plus, on a soit $C \in [A'A'']$, soit $B \in [A'A'']$, ce qui signifie que $B$ ou $C$ est à l'intérieur du $A$-cercle d'Apollonius. Puisque $B$ et $C$ sont chacun sur un des autres cercles, on a forcément deux points d'intersection.
$$\displaystyle \frac{|XB|}{|XC|} = \frac{|AB|}{|AC|} \quad \text{ et } \quad \frac{|XA|}{|XB|} = \frac{|CA|}{|CB|},$$ alors il suffit de multiplier les deux égalités pour obtenir la troisième :
$$\displaystyle \frac{|XA|}{|XC|} = \frac{|BA|}{|BC|}.$$ Or, on se convainc facilement que les cercles ne sont pas tangents ni disjoints. En effet, comme $|AB| \neq |AC|$ le $A$-cercle d'Apollonius est bien un cercle. De plus, on a soit $C \in [A'A'']$, soit $B \in [A'A'']$, ce qui signifie que $B$ ou $C$ est à l'intérieur du $A$-cercle d'Apollonius. Puisque $B$ et $C$ sont chacun sur un des autres cercles, on a forcément deux points d'intersection.
Dans le cas particulier où le triangle est équilatéral, les trois "cercles" sont les trois médiatrices du triangle et ils se rencontrent donc en un unique point.
2. Triangle podaire
Il existe un lien entre les cercles d'Apollonius et la notion de triangle podaire. Rappelons que si $ABC$ est un triangle et $P$ un point, le triangle podaire $A'B'C'$ est défini en considérant les projections de $P$ sur les trois côtés du triangle, comme dans la figure suivante.
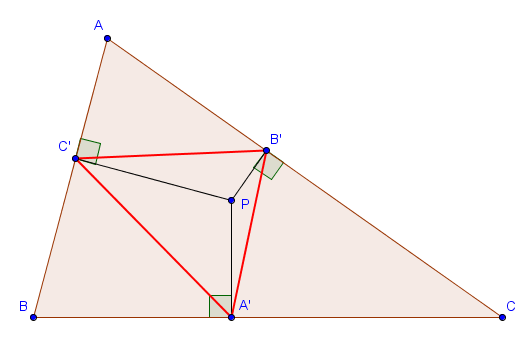
Comme nous l'avons déjà constaté, les longueurs des côtés de $A'B'C'$ sont données par les formules suivantes
$$|B'C'| = |PA| \cdot \sin \hat A, \quad |C'A'| = |PB| \cdot \sin \hat B, \quad |A'B'| = |PC| \cdot \sin \hat C.$$ On peut notamment en déduire que $|A'B'| = |A'C'|$ si et seulement si
$$1 = \frac{|A'B'|}{|A'C'|} = \frac{|PC| \cdot \sin \hat C}{|PB| \cdot \sin \hat B} = \frac{|PC|\cdot |AB|}{|PB| \cdot |AC|},$$ c'est-à-dire si et seulement si
$$\frac{|PC|}{|PB|} = \frac{|AC|}{|AB|}.$$ Nous venons donc de prouver le résultat suivant :
Il n'y aura bien sûr jamais un énoncé de géométrie contenant le terme Cercle d'Apollonius, mais l'intérêt de ceux-ci est que leur connaissance peut permettre de trouver plus rapidement une solution à un problème. Par exemple, si un triangle podaire est construit d'une façon ou d'une autre dans un énoncé (en projetant un même point $P$ sur plusieurs droites) et si celui-ci se révèle être isocèle, alors on peut directement en conclure que $P$ est sur le cercle d'Apollonius correspondant. On a donc un cercle passant par $P$ et plusieurs points remarquables, ce qui peut permettre de continuer avec une chasse aux angles, des puissances de points ou d'autres outils habituels...

Comme nous l'avons déjà constaté, les longueurs des côtés de $A'B'C'$ sont données par les formules suivantes
$$|B'C'| = |PA| \cdot \sin \hat A, \quad |C'A'| = |PB| \cdot \sin \hat B, \quad |A'B'| = |PC| \cdot \sin \hat C.$$ On peut notamment en déduire que $|A'B'| = |A'C'|$ si et seulement si
$$1 = \frac{|A'B'|}{|A'C'|} = \frac{|PC| \cdot \sin \hat C}{|PB| \cdot \sin \hat B} = \frac{|PC|\cdot |AB|}{|PB| \cdot |AC|},$$ c'est-à-dire si et seulement si
$$\frac{|PC|}{|PB|} = \frac{|AC|}{|AB|}.$$ Nous venons donc de prouver le résultat suivant :
Résultat
Soit $ABC$ un triangle et $P$ un point. Le triangle podaire $A'B'C'$ issu de $P$ est isocèle en $A'$ si et seulement si $P$ se situe sur le $A$-cercle d'Apollonius de $ABC$. En particulier, le triangle $A'B'C'$ est équilatéral si et seulement si $P$ est l'un des deux points d'intersection des trois cercles d'Apollonius.
Il n'y aura bien sûr jamais un énoncé de géométrie contenant le terme Cercle d'Apollonius, mais l'intérêt de ceux-ci est que leur connaissance peut permettre de trouver plus rapidement une solution à un problème. Par exemple, si un triangle podaire est construit d'une façon ou d'une autre dans un énoncé (en projetant un même point $P$ sur plusieurs droites) et si celui-ci se révèle être isocèle, alors on peut directement en conclure que $P$ est sur le cercle d'Apollonius correspondant. On a donc un cercle passant par $P$ et plusieurs points remarquables, ce qui peut permettre de continuer avec une chasse aux angles, des puissances de points ou d'autres outils habituels...
3. Droite de Lemoine
Nous avons vu comment obtenir un diamètre du $A$-cercle d'Apollonius : il suffit de prendre l'intersection de la bissectrice intérieure de $A$ avec $BC$ puis l'intersection de sa bissectrice extérieure avec $BC$. Le centre $O_A$ de ce cercle est donc pour le moment juste caractérisé comme étant le milieu de ce diamètre. En fait, ce centre peut être construit d'une autre manière : il se situe sur un des côtés du triangle tangentiel associé à $ABC$.
De la même façon, pourvu que $ABC$ n'est pas isocèle on peut construire le centre $O_B$ du $B$-cercle d'Apollonius et le centre $O_C$ du $C$-cercle d'Apollonius. Les trois centres sont alignés : cela découle du fait que les trois cercles ont exactement deux points communs. La droite de Lemoine est alors définie comme la droite passant par ces trois centres. Elle est représentée en rouge sur la figure suivante. Le cercle circonscrit au triangle $ABC$ ainsi que ses trois tangentes en $A$, $B$ et $C$ sont représenté en pointillés. Le triangle formé par ces trois tangentes est bien sûr le triangle tangentiel associé à $ABC$.
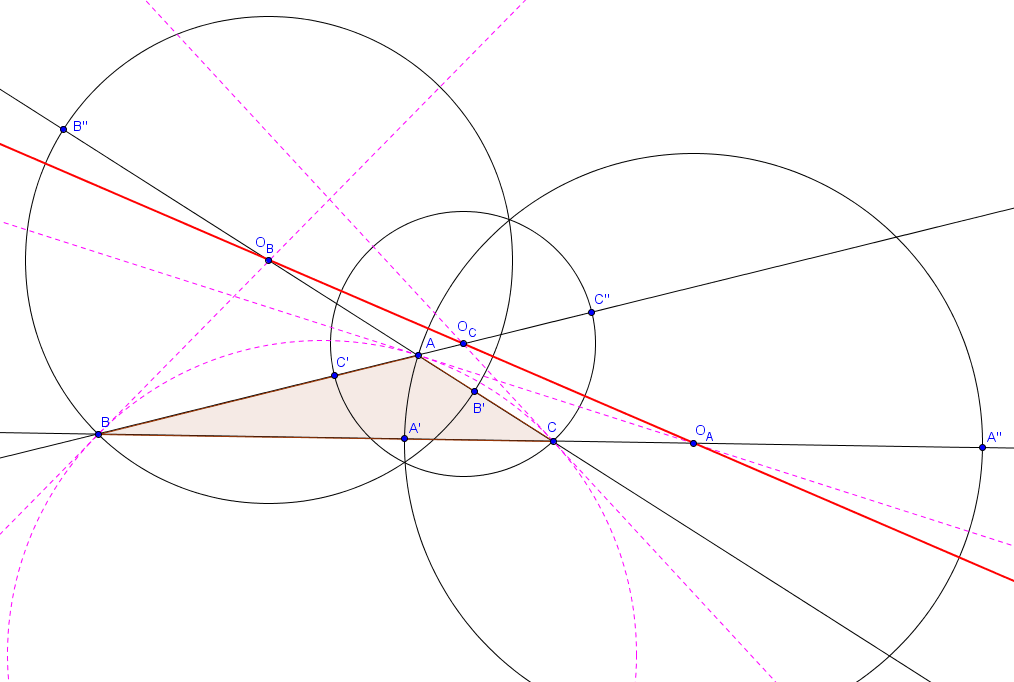
La droite de Lemoine porte le même nom que le point de Lemoine, que nous avons précédemment défini comme étant l'intersection des symédianes du triangle $ABC$. Cela n'est pas une coïncidence : en fait, la droite de Lemoine est la polaire du point de Lemoine par rapport au cercle circonscrit à $ABC$. (La définition de polaire est donnée dans ce chapitre).
Proposition (centre d'un cercle d'Apollonius)
Soit $ABC$ un triangle tel que $|AB| \neq |AC|$ et soit $\Gamma$ le cercle circonscrit à $ABC$. La tangente à $\Gamma$ en $A$ coupe la droite $BC$ en le centre du $A$-cercle d'Apollonius de $ABC$.
Démonstration
Notons $X$ l'intersection de la tangente à $\Gamma$ en $A$ avec la droite $BC$. On désire montrer que $X$ est le milieu de $[A'A'']$, où $A'$ est l'intersection de la bissectrice intérieure de $A$ avec $BC$ et $A''$ est l'intersection de la bissectrice extérieure de $A$ avec $BC$.
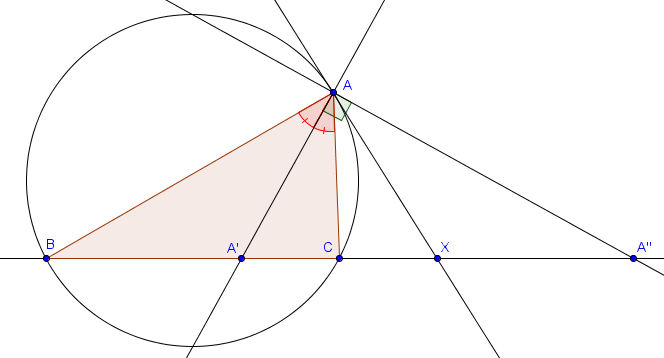
En utilisant l'égalité d'angles tangentiel et inscrit, on a
$$\widehat{XAA'} = \widehat{XAC} + \widehat{CAA'} = \widehat{ABC} + \widehat{A'AB} = 180^\circ - \widehat{AA'B} = \widehat{AA'C} = \widehat{AA'X}.$$ On en déduit que le triangle $AXA'$ est isocèle. Aussi, le triangle $AXA''$ est également isocèle puisque
$$\widehat{XA''A} = 90^\circ - \widehat{XA'A} = 90^\circ - \widehat{XAA'} = \widehat{XAA''}.$$ On a donc la suite d'égalités
$$|XA'| = |XA| = |XA''|,$$ ce qui signifie que $X$ est bien le milieu de $[A'A'']$ et donc le centre du $A$-cercle d'Apollonius.

En utilisant l'égalité d'angles tangentiel et inscrit, on a
$$\widehat{XAA'} = \widehat{XAC} + \widehat{CAA'} = \widehat{ABC} + \widehat{A'AB} = 180^\circ - \widehat{AA'B} = \widehat{AA'C} = \widehat{AA'X}.$$ On en déduit que le triangle $AXA'$ est isocèle. Aussi, le triangle $AXA''$ est également isocèle puisque
$$\widehat{XA''A} = 90^\circ - \widehat{XA'A} = 90^\circ - \widehat{XAA'} = \widehat{XAA''}.$$ On a donc la suite d'égalités
$$|XA'| = |XA| = |XA''|,$$ ce qui signifie que $X$ est bien le milieu de $[A'A'']$ et donc le centre du $A$-cercle d'Apollonius.
De la même façon, pourvu que $ABC$ n'est pas isocèle on peut construire le centre $O_B$ du $B$-cercle d'Apollonius et le centre $O_C$ du $C$-cercle d'Apollonius. Les trois centres sont alignés : cela découle du fait que les trois cercles ont exactement deux points communs. La droite de Lemoine est alors définie comme la droite passant par ces trois centres. Elle est représentée en rouge sur la figure suivante. Le cercle circonscrit au triangle $ABC$ ainsi que ses trois tangentes en $A$, $B$ et $C$ sont représenté en pointillés. Le triangle formé par ces trois tangentes est bien sûr le triangle tangentiel associé à $ABC$.

La droite de Lemoine porte le même nom que le point de Lemoine, que nous avons précédemment défini comme étant l'intersection des symédianes du triangle $ABC$. Cela n'est pas une coïncidence : en fait, la droite de Lemoine est la polaire du point de Lemoine par rapport au cercle circonscrit à $ABC$. (La définition de polaire est donnée dans ce chapitre).