Théorie > Géométrie > Puissances de points
Prérequis
Résumé
Nous présentons ici la notion de puissance d'un point par rapport à un cercle. Celle-ci joue un rôle dans la résolution de nombreux problèmes de géométrie, c'est pourquoi il faut toujours envisager cette piste, qu'elle soit suggérée par l'énoncé ou non, lorsqu'on essaye de résoudre un problème.
Ce chapitre a été écrit par N. Radu et mis en ligne le 8 décembre 2014.
1. Puissance
Étant donné un point et un cercle, on peut définir la puissance du point par rapport au cercle comme suit.
Remarquons déjà que, le cercle $\mathcal{C}$ étant fixé, la puissance de $X$ par rapport à $\mathcal{C}$ ne dépend que de la distance $|OX|$. On constate aussi qu'elle est nulle si $X$ appartient au cercle, strictement positive si $X$ se situe en dehors du cercle et strictement négative s'il se situe à l'intérieur.
Ce qui donne aux puissances de points leur intérêt est la proposition suivante.
Définition (puissance)
Soit $\mathcal{C}$ un cercle de centre $O$ et de rayon $R$, et $X$ un point. La puissance de $X$ par rapport à $\mathcal{C}$, notée $P_\mathcal{C}(X)$, est définie par
$$P_\mathcal{C}(X) = |OX|^2 - R^2.$$
$$P_\mathcal{C}(X) = |OX|^2 - R^2.$$
Remarquons déjà que, le cercle $\mathcal{C}$ étant fixé, la puissance de $X$ par rapport à $\mathcal{C}$ ne dépend que de la distance $|OX|$. On constate aussi qu'elle est nulle si $X$ appartient au cercle, strictement positive si $X$ se situe en dehors du cercle et strictement négative s'il se situe à l'intérieur.
Ce qui donne aux puissances de points leur intérêt est la proposition suivante.
Proposition
Soit $\mathcal{C}$ un cercle et $X$ un point. Soit $d$ une droite passant par $X$.
- Si $d$ intersecte $\mathcal{C}$ en deux points distincts $A$ et $B$, alors $P_\mathcal{C}(X) = \vec{XA}\cdot \vec{XB}$, c'est-à-dire
$$P_\mathcal{C}(X) = \left\{\begin{array}{cl}
|XA| \cdot |XB| & \text{ si } X \text{ est à l'extérieur de } \mathcal{C},\\
-|XA| \cdot |XB| & \text{ si } X \text{ est à l'intérieur de } \mathcal{C}.
\end{array}\right.$$ - Si la droite $d$ est tangente à $\mathcal{C}$ en $A$, alors
$$P_\mathcal{C}(X) = |XA|^2.$$
Démonstration
Nous allons démontrer ce résultat lorsque $X$ est à l'extérieur de $\mathcal{C}$. La preuve est similaire lorsque $X$ est à l'intérieur (et la deuxième situation n'arrive en fait jamais puisqu'une tangente n'a pas de points à l'intérieur du cercle).
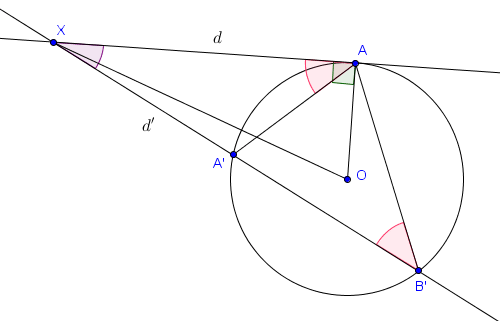
- Si $d$ passe par $X$ et est tangente à $\mathcal{C}$ en $A$, alors le triangle $XAO$ (où $O$ est le centre de $\mathcal{C}$) est rectangle en $A$. Par Pythagore, on a donc
$$|XA|^2 = |XO|^2 - |AO|^2 = |XO|^2 - R^2 = P_\mathcal{C}(X).$$ - Supposons maintenant, tout en gardant les notations du point précédent, avoir une autre droite $d'$ passant par $X$ mais intersectant $\mathcal{C}$ en deux points distincts $A'$ et $B'$. On suppose que $A'$ est plus proche de $X$ que $B'$. Les triangles $XA'A$ et $XAB'$ sont alors semblables. En effet, on a l'angle $\widehat{A'XA}$ en commun et $\widehat{XAA'} = \widehat{AB'A'}$ (angles tangentiel et inscrit interceptant le même arc $AA'$). On en déduit l'égalité
$$\frac{|XA'|}{|XA|} = \frac{|XA|}{|XB'|},$$ qui devient
$$|XA'|\cdot |XB'| = |XA|^2 = P_\mathcal{C}(X)$$ par le point précédent.

2. Axe radical
La notion d'axe radical de deux cercles est directement liée à celle de puissance de point :
Nous nous intéressons uniquement à des cercles de centres distincts. En effet, si au contraire $\mathcal{C}$ et $\mathcal{C'}$ avaient le même centre, alors soit les deux cercles seraient identiques auquel cas tous les points auraient bien sûr la même puissance par rapport à chaque cercle, soit les deux cercles seraient distincts et aucun point n'aurait la même puissance par rapport à $\mathcal{C}$ et $\mathcal{C}'$. Ces cas sont donc dégénérés et par conséquent peu intéressants.
Comme l'affirme la proposition suivante (que nous ne démontrons pas), l'axe radical de deux cercles prend en fait toujours la forme d'une droite.
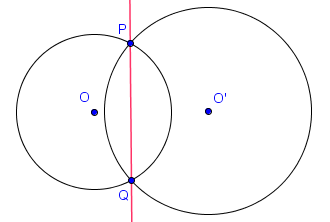
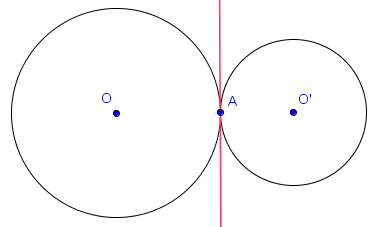
La partie non évidente de ce résultat est que l'axe radical prend la forme d'une droite. Par contre, celle-ci doit bien sûr être perpendiculaire à la droite passant par les deux centres, par symétrie de la situation. Aussi, on comprend facilement pourquoi, lorsque $X$ est un point commun à $\mathcal{C}$ et $\mathcal{C}'$, $X$ appartient à l'axe radical de ceux-ci. En effet, on a alors $P_\mathcal{C}(X) = 0 = P_{\mathcal{C}'}(X)$.
Il est donc facile, lorsque l'on est en présence de deux cercles ayant un ou deux points communs, de tracer leur axe radical. Par contre, lorsque les deux cercles sont disjoints, on sait juste qu'il s'agit d'une droite perpendiculaire à la droite passant par les deux centres.
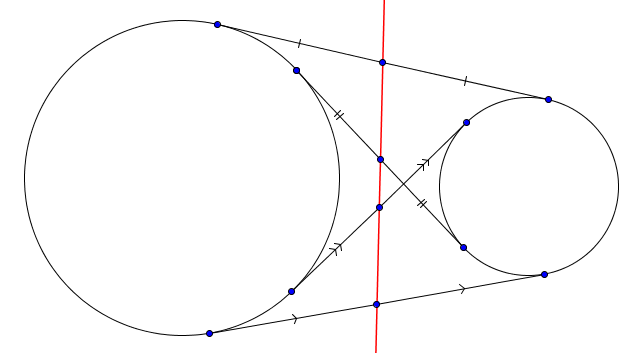
Définition (axe radical)
L'axe radical de deux cercles $\mathcal{C}$ et $\mathcal{C}'$ de centres distincts est le lieu des points dont la puissance par rapport à $\mathcal{C}$ est égale à celle par rapport à $\mathcal{C'}$, c'est-à-dire
$$\left\{X \ \mid \ P_\mathcal{C}(X) = P_{\mathcal{C}'}(X)\right\}.$$
$$\left\{X \ \mid \ P_\mathcal{C}(X) = P_{\mathcal{C}'}(X)\right\}.$$
Nous nous intéressons uniquement à des cercles de centres distincts. En effet, si au contraire $\mathcal{C}$ et $\mathcal{C'}$ avaient le même centre, alors soit les deux cercles seraient identiques auquel cas tous les points auraient bien sûr la même puissance par rapport à chaque cercle, soit les deux cercles seraient distincts et aucun point n'aurait la même puissance par rapport à $\mathcal{C}$ et $\mathcal{C}'$. Ces cas sont donc dégénérés et par conséquent peu intéressants.
Comme l'affirme la proposition suivante (que nous ne démontrons pas), l'axe radical de deux cercles prend en fait toujours la forme d'une droite.
Proposition
Soient $\mathcal{C}$ et $\mathcal{C}'$ deux cercles de centres distincts. L'axe radical de $\mathcal{C}$ et $\mathcal{C'}$ est une droite perpendiculaire à la droite passant par les centres de $\mathcal{C}$ et $\mathcal{C}'$. De plus,
- si les cercles se rencontrent en deux points distincts $P$ et $Q$, alors l'axe radical est exactement la droite $PQ$.
- si les cercles sont tangents en un point $A$, alors l'axe radical passe par $A$.


La partie non évidente de ce résultat est que l'axe radical prend la forme d'une droite. Par contre, celle-ci doit bien sûr être perpendiculaire à la droite passant par les deux centres, par symétrie de la situation. Aussi, on comprend facilement pourquoi, lorsque $X$ est un point commun à $\mathcal{C}$ et $\mathcal{C}'$, $X$ appartient à l'axe radical de ceux-ci. En effet, on a alors $P_\mathcal{C}(X) = 0 = P_{\mathcal{C}'}(X)$.
Il est donc facile, lorsque l'on est en présence de deux cercles ayant un ou deux points communs, de tracer leur axe radical. Par contre, lorsque les deux cercles sont disjoints, on sait juste qu'il s'agit d'une droite perpendiculaire à la droite passant par les deux centres.
Tangentes communes
Il est tout de même possible, lorsque deux cercles sont disjoints mais extérieurs, de tracer leur axe radical à l'aide du résultat suivant (qu'il ne faut pas perdre de vue puisqu'il intervient parfois dans la résolution de problèmes).Propriété
Soient $\mathcal{C}$ et $\mathcal{C}'$ des cercles de centres distincts. Pour toute droite $AA'$ tangente à $\mathcal{C}$ en $A$ et à $\mathcal{C}'$ en $A'$, l'axe radical des deux cercles coupe le segment $[AA']$ en son milieu.

Démonstration
Ce résultat est en fait presque évident. En effet, si $X$ dénote le point d'intersection de l'axe radical avec $AA'$, on sait par une formule précédemment donnée que la puissance de $X$ par rapport à $\mathcal{C}$ est égale à $|XA|^2$ et que la puissance de $X$ par rapport à $\mathcal{C}'$ est égale à $|XA'|^2$. Or, puisque $X$ est sur l'axe radical des deux cercles, les deux puissances doivent être égales et on a $|XA| = |XA'|$.
3. Centre radical
Si maintenant nous ne sommes plus en présence d'un ou deux cercles, mais bien trois, alors on peut mettre en évidence un point particulier appelé centre radical des trois cercles.
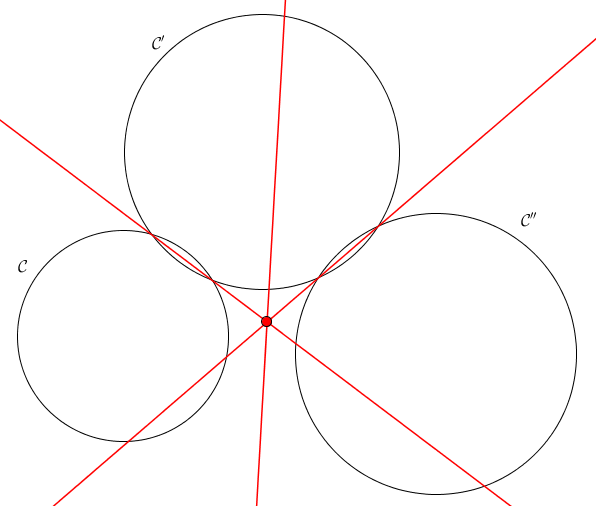
Proposition (définition du centre radical)
Soient $\mathcal{C}$, $\mathcal{C}'$ et $\mathcal{C}''$ trois cercles de centres non alignés. Les axes radicaux de ces trois cercles pris deux à deux sont concourants : ils se rencontrent en un unique point appelé centre radical de $\mathcal{C}$, $\mathcal{C}'$ et $\mathcal{C}''$.

Démonstration
Considérons $d_1$ l'axe radical de $\mathcal{C}$ et $\mathcal{C}'$, et $d_2$ l'axe radical de $\mathcal{C}'$ et $\mathcal{C}''$. Les droites $d_1$ et $d_2$ ne sont pas parallèles puisque les centres des trois cercles ne sont pas alignés. Elles se rencontrent dès lors en un point que l'on note $X$. Il suffit de montrer que $X$ se situe sur l'axe radical de $\mathcal{C}$ et $\mathcal{C}''$. Cela est en fait évident, puisqu'on a
$$P_\mathcal{C}(X) = P_{\mathcal{C}'}(X) = P_{\mathcal{C}''}(X).$$
$$P_\mathcal{C}(X) = P_{\mathcal{C}'}(X) = P_{\mathcal{C}''}(X).$$
Quadrilatère cyclique
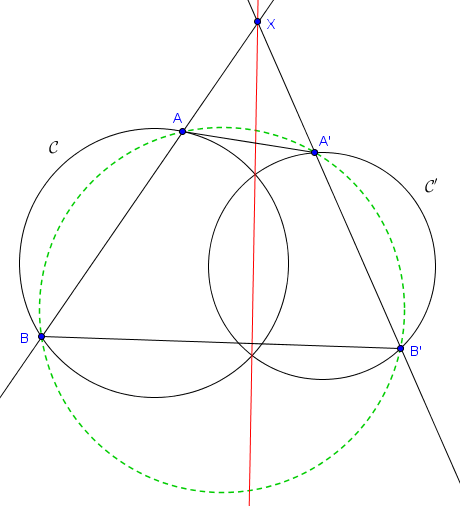
Il est également possible de raisonner dans un sens plutôt contraire. À partir d'un point sur l'axe radical de deux cercles, on peut tracer deux droites intersectant chacune un des cercles en deux points. Les quatre points ainsi obtenus sont alors sur un même cercle, comme l'indique le résultat suivant.Propriété
Soient $\mathcal{C}$ et $\mathcal{C}'$ deux cercles, et $X$ un point sur l'axe radical de ces deux cercles. Soit $d$ une droite passant par $X$ coupant $\mathcal{C}$ en deux points distincts $A$ et $B$ et $d'$ une droite passant par $X$ coupant $\mathcal{C}'$ en deux points distincts $A'$ et $B'$. Alors le quadrilatère $ABB'A'$ est cyclique.

Démonstration
Vu que $X$ est sur l'axe radical de $\mathcal{C}$ et $\mathcal{C}'$, sa puissance est la même par rapport à ces deux cercles. On a donc
$$|XA|\cdot |XB| = |XA'|\cdot |XB'|.$$ Ecrit autrement, on a
$$\frac{|XA|}{|XA'|} = \frac{|XB'|}{|XB|}.$$ Cela signifie que les triangles $XAA'$ et $XB'B$ sont semblables. En particulier, on a $\widehat{XAA'} = \widehat{XB'B}$, et donc $\widehat{BAA'} + \widehat{BB'A'} = 180^\circ$, ce qui prouve que le quadrilatère $ABB'A'$ est cyclique.
Bien sûr, le point $X$ est alors le centre radical des trois cercles tracés sur la figure.
$$|XA|\cdot |XB| = |XA'|\cdot |XB'|.$$ Ecrit autrement, on a
$$\frac{|XA|}{|XA'|} = \frac{|XB'|}{|XB|}.$$ Cela signifie que les triangles $XAA'$ et $XB'B$ sont semblables. En particulier, on a $\widehat{XAA'} = \widehat{XB'B}$, et donc $\widehat{BAA'} + \widehat{BB'A'} = 180^\circ$, ce qui prouve que le quadrilatère $ABB'A'$ est cyclique.
Bien sûr, le point $X$ est alors le centre radical des trois cercles tracés sur la figure.