Inversion et polarisation
Théorème de Ptolémée
Comme mentionné précédemment, une manière d'utiliser l'inversion dans la résolution d'un problème consiste à appliquer une inversion (bien choisie) à l'entièreté de la figure et à travailler sur la nouvelle figure obtenue plutôt que sur l'originale. L'idée d'appliquer une inversion de cette façon peut venir lorsque l'on est en présence d'une figure contenant beaucoup de cercles. En effet, une inversion pourrait alors transformer certains de ceux-ci en droites et faciliter les raisonnements.
Pour illustrer cette méthode, nous allons démontrer les deux sens du théorème de Ptolémée à l'aide d'une inversion. Rappelons son énoncé :
Nous avions donné la démonstration du sens $\Rightarrow$ dans le chapitre sur les quadrilatères cycliques, mais le sens $\Leftarrow$ n'avait pas été donné car il est difficile à démontrer sans faire usage d'une inversion. Ceci montre bien la puissance d'une telle méthode.
Nous démontrons les deux sens du théorème de Ptolémée d'un seul coup.
Pour illustrer cette méthode, nous allons démontrer les deux sens du théorème de Ptolémée à l'aide d'une inversion. Rappelons son énoncé :
Théorème de Ptolémée
Un quadrilatère (non croisé) $ABCD$ est cyclique si et seulement si
$$|AC|\cdot |BD| = |AB| \cdot |CD| + |BC| \cdot |AD|,$$ c'est-à-dire si le produit des longueurs de ses diagonales est égal à la somme des produits des longueurs des côtés opposés.
$$|AC|\cdot |BD| = |AB| \cdot |CD| + |BC| \cdot |AD|,$$ c'est-à-dire si le produit des longueurs de ses diagonales est égal à la somme des produits des longueurs des côtés opposés.
Nous avions donné la démonstration du sens $\Rightarrow$ dans le chapitre sur les quadrilatères cycliques, mais le sens $\Leftarrow$ n'avait pas été donné car il est difficile à démontrer sans faire usage d'une inversion. Ceci montre bien la puissance d'une telle méthode.
Nous démontrons les deux sens du théorème de Ptolémée d'un seul coup.
Démonstration
Considérons l'inversion de centre $A$ et de rapport $1$. Les images des points $B$, $C$ et $D$ sont notées $B'$, $C'$ et $D'$, comme sur la figure suivante.
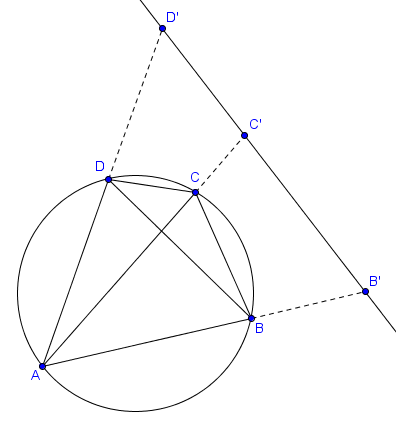
Les points $A, B, C, D$ sont cocycliques si et seulement si les points $B'$, $C'$ et $D'$ sont alignés. Cela vient en effet du fait que l'image d'un cercle passant par $A$ par une inversion de centre $A$ est une droite ne passant pas par $A$ (et vice versa). Or, le fait que $B'$, $C'$ et $D'$ sont alignés peut se traduire par l'égalité $|B'C'|+|C'D'|=|B'D'|$. Nous calculons alors les longueurs $|B'C'|$, $|C'D'|$ et $|B'D'|$ en fonctions des points $A, B, C, D$.
Les triangles $ABC$ et $AC'B'$ sont semblables, ce qui se traduit par
$$\frac{|B'C'|}{|BC|} = \frac{|AB'|}{|AC|}.$$ Comme $|AB'| \cdot |AB| = 1$ (car on considère l'inversion de centre $A$ et de rapport $1$), il s'ensuit que
$$|B'C'| = \frac{|BC|}{|AC| \cdot |AB|}.$$ De la même façon, les triangles $ACD$ et $AD'C'$ sont semblables ainsi que les triangles $ABD$ et $AD'B'$. On obtient donc similairement que
$$|C'D'| = \frac{|CD|}{|AC| \cdot |AD|} \quad \text{et}\quad |B'D'| = \frac{|BD|}{|AB| \cdot |AD|}.$$ L'égalité $|B'D'| = |B'C'|+|C'D'|$ est alors équivalente à
$$\frac{|BC|}{|AC| \cdot |AB|} + \frac{|CD|}{|AC| \cdot |AD|} = \frac{|BD|}{|AB| \cdot |AD|},$$ qui est elle-même équivalente (en la multipliant par $|AB| \cdot |AC| \cdot |AD|$) à
$$|BC| \cdot |AD| + |CD| \cdot |AB| = |BD| \cdot |AC|.$$

Les points $A, B, C, D$ sont cocycliques si et seulement si les points $B'$, $C'$ et $D'$ sont alignés. Cela vient en effet du fait que l'image d'un cercle passant par $A$ par une inversion de centre $A$ est une droite ne passant pas par $A$ (et vice versa). Or, le fait que $B'$, $C'$ et $D'$ sont alignés peut se traduire par l'égalité $|B'C'|+|C'D'|=|B'D'|$. Nous calculons alors les longueurs $|B'C'|$, $|C'D'|$ et $|B'D'|$ en fonctions des points $A, B, C, D$.
Les triangles $ABC$ et $AC'B'$ sont semblables, ce qui se traduit par
$$\frac{|B'C'|}{|BC|} = \frac{|AB'|}{|AC|}.$$ Comme $|AB'| \cdot |AB| = 1$ (car on considère l'inversion de centre $A$ et de rapport $1$), il s'ensuit que
$$|B'C'| = \frac{|BC|}{|AC| \cdot |AB|}.$$ De la même façon, les triangles $ACD$ et $AD'C'$ sont semblables ainsi que les triangles $ABD$ et $AD'B'$. On obtient donc similairement que
$$|C'D'| = \frac{|CD|}{|AC| \cdot |AD|} \quad \text{et}\quad |B'D'| = \frac{|BD|}{|AB| \cdot |AD|}.$$ L'égalité $|B'D'| = |B'C'|+|C'D'|$ est alors équivalente à
$$\frac{|BC|}{|AC| \cdot |AB|} + \frac{|CD|}{|AC| \cdot |AD|} = \frac{|BD|}{|AB| \cdot |AD|},$$ qui est elle-même équivalente (en la multipliant par $|AB| \cdot |AC| \cdot |AD|$) à
$$|BC| \cdot |AD| + |CD| \cdot |AB| = |BD| \cdot |AC|.$$