Pavages
Prérequis
Résumé
Les problèmes de pavages constituent une classe de problèmes assez particulière. Ils consistent à paver une surface donnée à l'aide de certains pavés de forme donnée, et le tout est généralement de montrer qu'un tel pavage est impossible. Nous présentons ici les différentes méthodes permettant de résoudre ce type de problème.
Ce chapitre a été écrit par N. Radu et mis en ligne le 8 décembre 2014.
1. Coloriage
Voici un exemple classique de problème de pavage.
La première attitude face à un tel problème est évidemment d'essayer d'effectuer un tel pavage. On se rend cependant vite compte que cela n'est pas possible, et vient alors le moment de le prouver. Un élève n'ayant jamais rencontré de problèmes similaires sera peut-être tenté de discuter différents cas : "Si je place un pavé dans le sens horizontal dans ce coin, alors je dois en placer un autre dans ce sens...". Un tel raisonnement n'a cependant aucune chance d'aboutir dans ce cas vu le grand nombre de pavés qui doivent être placés.
Une méthode évidente pour prouver qu'un pavage est impossible est simplement de voir si l'aire d'un pavé divise l'aire de la surface totale. Ici, la surface totale est constituée de $62$ petits carrés, alors qu'un pavé permet de recouvrir $2$ petits carrés. On ne trouve donc pas dans ce cas d'absurdité, mais on sait déjà que, si un pavage existe, alors il est constitué de $\frac{62}{2} = 31$ pavés.
Une autre méthode plus prometteuse pour ce genre de problème est le coloriage. Elle consiste à colorier les différentes cases de la surface à paver de manière astucieuse, de sorte à prouver la non-existence d'un pavage. Pour notre exemple, le coloriage est en fait même suggéré par l'énoncé puisqu'un échiquier possède un coloriage naturel :

Ce coloriage peut sembler bien anodin, mais il permet en fait de résoudre directement le problème ! En effet, ce coloriage a de particulier que n'importe quel pavé $1 \times 2$ recouvre exactement un petit carré noir et un petit carré blanc. Or, on constate que la surface contient $32$ carrés blancs pour $30$ carrés noirs : il est donc clairement impossible d'effectuer un pavage correct !
Un simple coloriage permet donc de prouver très facilement qu'un pavage est impossible, alors qu'il semble difficile de conclure sans utiliser cette astuce. Le coloriage "en échiquier" est souvent performant, mais il faut parfois adapter le coloriage selon la surface et le type de pavé. Il n'est notamment pas interdit d'utiliser plus de deux couleurs, comme nous le verrons par la suite...
Problème
Est-il possible de paver entièrement et sans recouvrement un échiquier $8 \times 8$ dont deux coins opposés ont été retirés à l'aide de pavés de la forme $1 \times 2$ (dont les côtés doivent être parallèles aux côtés de l'échiquier) ?
La première attitude face à un tel problème est évidemment d'essayer d'effectuer un tel pavage. On se rend cependant vite compte que cela n'est pas possible, et vient alors le moment de le prouver. Un élève n'ayant jamais rencontré de problèmes similaires sera peut-être tenté de discuter différents cas : "Si je place un pavé dans le sens horizontal dans ce coin, alors je dois en placer un autre dans ce sens...". Un tel raisonnement n'a cependant aucune chance d'aboutir dans ce cas vu le grand nombre de pavés qui doivent être placés.
Une méthode évidente pour prouver qu'un pavage est impossible est simplement de voir si l'aire d'un pavé divise l'aire de la surface totale. Ici, la surface totale est constituée de $62$ petits carrés, alors qu'un pavé permet de recouvrir $2$ petits carrés. On ne trouve donc pas dans ce cas d'absurdité, mais on sait déjà que, si un pavage existe, alors il est constitué de $\frac{62}{2} = 31$ pavés.
Une autre méthode plus prometteuse pour ce genre de problème est le coloriage. Elle consiste à colorier les différentes cases de la surface à paver de manière astucieuse, de sorte à prouver la non-existence d'un pavage. Pour notre exemple, le coloriage est en fait même suggéré par l'énoncé puisqu'un échiquier possède un coloriage naturel :

Ce coloriage peut sembler bien anodin, mais il permet en fait de résoudre directement le problème ! En effet, ce coloriage a de particulier que n'importe quel pavé $1 \times 2$ recouvre exactement un petit carré noir et un petit carré blanc. Or, on constate que la surface contient $32$ carrés blancs pour $30$ carrés noirs : il est donc clairement impossible d'effectuer un pavage correct !
Un simple coloriage permet donc de prouver très facilement qu'un pavage est impossible, alors qu'il semble difficile de conclure sans utiliser cette astuce. Le coloriage "en échiquier" est souvent performant, mais il faut parfois adapter le coloriage selon la surface et le type de pavé. Il n'est notamment pas interdit d'utiliser plus de deux couleurs, comme nous le verrons par la suite...
2. Cases deux à deux non recouvrables
Pour illustrer une autre méthode, examinons un autre problème classique.
Encore une fois, quelques essais suffisent à se convaincre qu'il ne va pas être possible de paver le carré $3 \times 3$ à l'aide de ces pavés. On peut également compter que si un tel pavage existait, alors il serait constitué de $\frac{9}{3} = 3$ pavés. Comme le nombre de pavés est assez réduit, il est cette fois envisageable de traiter les différents cas, mais cela reste laborieux et le risque d'effectuer une erreur est assez grand.
Au vu de la section précédente, on peut aussi être tenté de colorier le carré $3 \times 3$. Le problème est qu'ici, chaque pavé recouvre $3$ cases. Il faudrait donc pour bien faire utiliser trois couleurs, mais on remarque vite qu'il n'est pas possible de trouver un coloriage pour lequel n'importe quel pavé recouvrirait forcément trois cases de couleurs distinctes. La méthode du coloriage ne semble donc pas efficace face à ce problème.
Il existe une autre méthode permettant de démontrer la non-existence d'un pavage. Dans notre exemple, on a remarqué qu'un éventuel pavage serait constitué d'exactement trois pavés. Or, le carré $3 \times 3$ possède $4$ coins, et l'astuce est de constater que deux coins différents ne peuvent pas être recouverts par un seul et même pavé ! Il est donc impossible, à l'aide d'uniquement $3$ pavés, de recouvrir les $4$ coins de notre surface, et nous avons par conséquent montré que le pavage était impossible.
De manière plus générale, cette méthode consiste, si le nombre de pavés est égal à $n$, à mettre en évidence $(n+1)$ cases qui sont deux à deux non recouvrables par un seul et même pavé. Observons par exemple le problème suivant :
En fait, dans ce dernier exemple, la méthode du coloriage aurait pu également fonctionner (et on voit facilement que les méthodes sont équivalentes) :
Dans la preuve précédente, il aurait même été possible de conclure en n'exhibant que les cases rouges, à l'aide du principe des tiroirs ! On se rend effectivement compte que chaque pavé $1 \times 6$ recouvre exactement une case rouge, et on a $11$ telles cases. En supposant qu'un pavage existe, on a donc $12$ chaussettes (pavés) dans $11$ tiroirs (cases rouges), et le principe des tiroirs nous indique qu'il y a au moins deux chaussettes dans le même tiroir, c'est-à-dire au moins deux pavés recouvrant la même case rouge, ce qui est impossible puisqu'on ne veut aucun recouvrement.
Problème
Est-il possible de paver entièrement et sans recouvrement un carré de $3 \times 3$ cases à l'aide de pavés de la forme suivante ?


Encore une fois, quelques essais suffisent à se convaincre qu'il ne va pas être possible de paver le carré $3 \times 3$ à l'aide de ces pavés. On peut également compter que si un tel pavage existait, alors il serait constitué de $\frac{9}{3} = 3$ pavés. Comme le nombre de pavés est assez réduit, il est cette fois envisageable de traiter les différents cas, mais cela reste laborieux et le risque d'effectuer une erreur est assez grand.
Au vu de la section précédente, on peut aussi être tenté de colorier le carré $3 \times 3$. Le problème est qu'ici, chaque pavé recouvre $3$ cases. Il faudrait donc pour bien faire utiliser trois couleurs, mais on remarque vite qu'il n'est pas possible de trouver un coloriage pour lequel n'importe quel pavé recouvrirait forcément trois cases de couleurs distinctes. La méthode du coloriage ne semble donc pas efficace face à ce problème.
Il existe une autre méthode permettant de démontrer la non-existence d'un pavage. Dans notre exemple, on a remarqué qu'un éventuel pavage serait constitué d'exactement trois pavés. Or, le carré $3 \times 3$ possède $4$ coins, et l'astuce est de constater que deux coins différents ne peuvent pas être recouverts par un seul et même pavé ! Il est donc impossible, à l'aide d'uniquement $3$ pavés, de recouvrir les $4$ coins de notre surface, et nous avons par conséquent montré que le pavage était impossible.
De manière plus générale, cette méthode consiste, si le nombre de pavés est égal à $n$, à mettre en évidence $(n+1)$ cases qui sont deux à deux non recouvrables par un seul et même pavé. Observons par exemple le problème suivant :
Problème
Est-il possible de paver entièrement et sans recouvrement un rectangle de $8 \times 9$ cases à l'aide de pavés rectangulaires $1 \times 6$ ?
Solution via cette méthode
Le nombre de pavés doit être égal à $\frac{72}{6} = 12$. Pour appliquer la méthode que nous venons de présenter, il faudrait donc trouver $13$ cases dont deux différentes ne peuvent jamais être recouvertes par un seul pavé $1 \times 6$. On peut en fait facilement trouver les cases suivantes (en orange) :
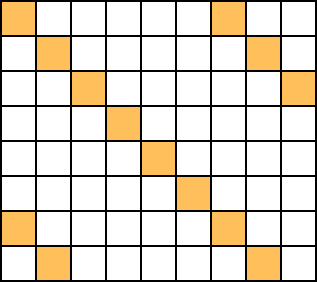
Puisque dans chaque ligne et chaque colonne, il n'y a jamais deux cases oranges situées dans un même rectangle $1 \times 6$, ces cases sont deux à deux non recouvrables par un même pavé de cette forme. On en déduit qu'il n'existe pas de pavage du rectangle $8 \times 9$ comme demandé.
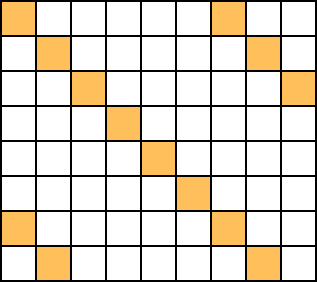
Puisque dans chaque ligne et chaque colonne, il n'y a jamais deux cases oranges situées dans un même rectangle $1 \times 6$, ces cases sont deux à deux non recouvrables par un même pavé de cette forme. On en déduit qu'il n'existe pas de pavage du rectangle $8 \times 9$ comme demandé.
En fait, dans ce dernier exemple, la méthode du coloriage aurait pu également fonctionner (et on voit facilement que les méthodes sont équivalentes) :
Démonstration via un coloriage
On considère le coloriage suivant.

Chaque pavé $1 \times 6$ recouvre six cases de couleurs différentes, et il y a $13$ cases oranges, $13$ cases bleues, $12$ cases vertes, $12$ cases mauves, $11$ cases rouges et $11$ cases blanches. Cela suffit pour conclure qu'un pavage est impossible.

Chaque pavé $1 \times 6$ recouvre six cases de couleurs différentes, et il y a $13$ cases oranges, $13$ cases bleues, $12$ cases vertes, $12$ cases mauves, $11$ cases rouges et $11$ cases blanches. Cela suffit pour conclure qu'un pavage est impossible.
Dans la preuve précédente, il aurait même été possible de conclure en n'exhibant que les cases rouges, à l'aide du principe des tiroirs ! On se rend effectivement compte que chaque pavé $1 \times 6$ recouvre exactement une case rouge, et on a $11$ telles cases. En supposant qu'un pavage existe, on a donc $12$ chaussettes (pavés) dans $11$ tiroirs (cases rouges), et le principe des tiroirs nous indique qu'il y a au moins deux chaussettes dans le même tiroir, c'est-à-dire au moins deux pavés recouvrant la même case rouge, ce qui est impossible puisqu'on ne veut aucun recouvrement.
3. Construction générale
Il arrive aussi qu'il faille donner une façon générale de paver certaines surfaces dont les dimensions sont variables. C'est généralement par une sorte de récurrence que l'on peut donner une telle construction. Illustrons cela avec le problème suivant :
Problème
Pour quels $m, n \in \mathbb{N}_0$ est-il possible de paver entièrement et sans recouvrement un rectangle $m \times n$ à l'aide des pavés suivants (pouvant éventuellement être retournés) ?
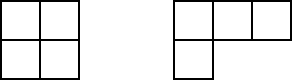
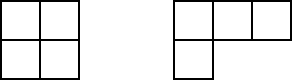
Solution
Vu que les deux pavés contiennent $4$ petits carrés, on voit déjà qu'il faut que $mn$ soit un multiple de $4$ pour avoir une chance que le rectangle $m \times n$ puisse être correctement recouvert. Examinons à présent ces cas où $mn$ est effectivement multiple de $4$
Si $m$ et $n$ sont tous les deux pairs, alors on peut simplement paver le rectangle $m \times n$ grâce aux pavés de forme carrée $2 \times 2$. Le seul cas un peu plus compliqué est donc celui où $m$ est multiple de $4$ et $n$ est impair (ou le contraire, ce cas étant évidemment pareil).
Si $n = 1$, le pavage est bien sûr impossible. Le plus petit cas intéressant est donc le rectangle $4 \times 3$. Après un peu de recherche, on trouve aisément que ce rectangle peut être pavé, par exemple comme suit :

On peut maintenant construire un pavage du rectangle $4 \times n$ pour tout $n$ impair supérieur ou égal à $3$ : il suffit de rajouter des pièces $2 \times 2$ pour compléter le pavage $4 \times 3$ donné ci-dessus. On peut même conclure pour les rectangles $m \times n$ avec $m$ multiple de $4$ et $n$ impair supérieur ou égal à $3$, puisqu'il suffit de mettre côte à côte les pavages trouvés pour un rectangle $4 \times n$.
En conclusion, les seuls rectangles $m \times n$ pour lesquels il n'existe pas de pavage sont ceux avec $mn$ non multiple de $4$ ou ceux avec $m = 1$ ou $n = 1$.
Si $m$ et $n$ sont tous les deux pairs, alors on peut simplement paver le rectangle $m \times n$ grâce aux pavés de forme carrée $2 \times 2$. Le seul cas un peu plus compliqué est donc celui où $m$ est multiple de $4$ et $n$ est impair (ou le contraire, ce cas étant évidemment pareil).
Si $n = 1$, le pavage est bien sûr impossible. Le plus petit cas intéressant est donc le rectangle $4 \times 3$. Après un peu de recherche, on trouve aisément que ce rectangle peut être pavé, par exemple comme suit :

On peut maintenant construire un pavage du rectangle $4 \times n$ pour tout $n$ impair supérieur ou égal à $3$ : il suffit de rajouter des pièces $2 \times 2$ pour compléter le pavage $4 \times 3$ donné ci-dessus. On peut même conclure pour les rectangles $m \times n$ avec $m$ multiple de $4$ et $n$ impair supérieur ou égal à $3$, puisqu'il suffit de mettre côte à côte les pavages trouvés pour un rectangle $4 \times n$.
En conclusion, les seuls rectangles $m \times n$ pour lesquels il n'existe pas de pavage sont ceux avec $mn$ non multiple de $4$ ou ceux avec $m = 1$ ou $n = 1$.