Convexité et inégalité de Jensen
Prérequis
Résumé
À partir de l'allure du graphe d'une fonction, on peut dire qu'elle est convexe ou concave. Nous donnons ici dans un premier temps les définitions rigoureuses de ces notions. La concavité d'une fonction peut en fait être exploitée dans des problèmes d'inégalités via l'inégalité de Jensen : c'est l'objet de ce chapitre.
Ce chapitre a été écrit par B. Legat et N. Radu et mis en ligne le 8 décembre 2014.
1. Ensembles convexes
Avant de définir les fonctions convexes, on introduit la notion d'ensemble convexe.
On remarque que pour $\lambda = 0$, $\lambda x + (1-\lambda) y = y$ et pour $\lambda = 1$, $\lambda x + (1-\lambda) y = x$. Géométriquement, les valeurs intermédiaires de $\lambda$ donnent tous les points du segment de droite entre $x$ et $y$. La condition signifie donc que tout segment de droite reliant deux points de $A$ est entièrement contenu dans $A$. Pour $\lambda = \frac{1}{2}$, on a d'ailleurs la moyenne arithmétique de $x$ et $y$, c'est-à-dire le milieu des deux points.
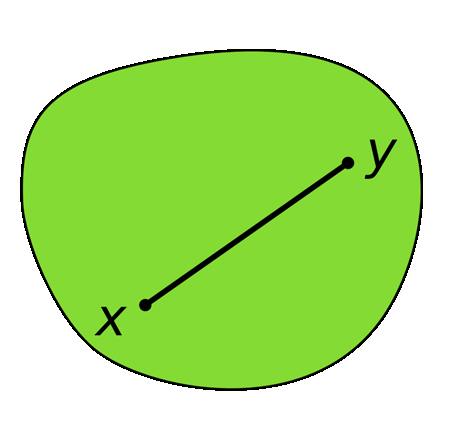
Exemple d'ensemble convexe.
On dit par ailleurs qu'un sous-ensemble de $\mathbb{R}^2$ est concave s'il n'est pas convexe.
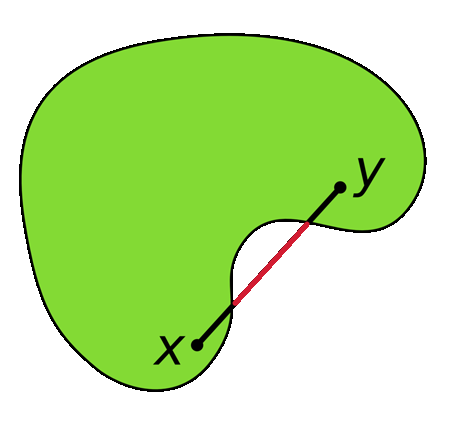
Exemple d'ensemble concave.
Exemple : Le disque $D = \{(x,y)\in \mathbb{R}^2 | x^2 + y^2 \leq 1\}$ est convexe.
Définition
Un ensemble $A \subseteq \mathbb{R}^2$ est dit convexe si pour tous $x, y\in A$ et tout $\lambda \in [0, 1]$, on a
$$\lambda x + (1-\lambda) y \in A.$$
$$\lambda x + (1-\lambda) y \in A.$$
On remarque que pour $\lambda = 0$, $\lambda x + (1-\lambda) y = y$ et pour $\lambda = 1$, $\lambda x + (1-\lambda) y = x$. Géométriquement, les valeurs intermédiaires de $\lambda$ donnent tous les points du segment de droite entre $x$ et $y$. La condition signifie donc que tout segment de droite reliant deux points de $A$ est entièrement contenu dans $A$. Pour $\lambda = \frac{1}{2}$, on a d'ailleurs la moyenne arithmétique de $x$ et $y$, c'est-à-dire le milieu des deux points.

Exemple d'ensemble convexe.
On dit par ailleurs qu'un sous-ensemble de $\mathbb{R}^2$ est concave s'il n'est pas convexe.

Exemple d'ensemble concave.
Exemple : Le disque $D = \{(x,y)\in \mathbb{R}^2 | x^2 + y^2 \leq 1\}$ est convexe.
2. Fonctions convexes
On peut maintenant définir ce qu'est une fonction convexe.
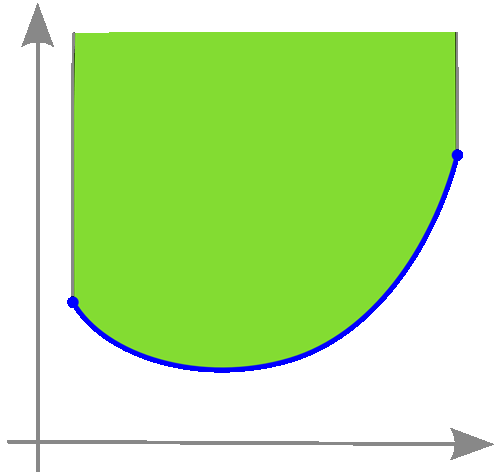
Exemple de fonction convexe.
Une manière équivalente de définir la convexité est de dire qu'une fonction $f:I\subseteq\mathbb{R}\to\mathbb{R}$ est convexe sur $I$ si pour tous $a,b \in I$ et tout $\lambda \in [0,1]$, on a
$$f(\lambda a + (1-\lambda) b) \leq \lambda f(a) + (1-\lambda) f(b).$$ On remarque en effet que
$$(\lambda a + (1-\lambda) b, \lambda f(a) + (1-\lambda) f(b)) = \lambda (a, f(a)) + (1-\lambda) (b, f(b))$$ est le point du segment de droite reliant $(a,f(a))$ à $(b,f(b))$ d'abscisse $\lambda a + (1-\lambda) b$. Par ailleurs, $f(\lambda a + (1-\lambda) b)$ est la valeur de la fonction $f$ en ce même point. L'inégalité signifie donc que les segments de droite reliant deux points du graphe de $f$ ont tous leurs points au dessus du graphe.
Une fonction est par contre dite concave si l'ensemble des points en dessous du graphe de $f$ forme un ensemble convexe. Attention : cela ne revient pas à demander que l'ensemble des points au dessus du graphe est concave ! Contrairement aux ensembles qui sont soit convexes, soit concaves, il existe donc des fonctions qui ne sont ni convexes ni concaves.
Lors d'une compétition, il n'est cependant pas réellement nécessaire de prouver qu'une fonction basique est concave ou convexe. En effet, on sait qu'il suffit de dériver deux fois la fonction pour démontrer qu'elle est convexe ou concave, ce qui se fait de manière automatique.
En pratique, on dessine le graphe de la fonction pour voir si elle est convexe ou concave en regardant l'ensemble délimité par le graphe. Il n'est donc pas important de connaître les dérivées : il faut juste retenir que la convexité ou concavité d'une fonction peut être vérifiée rigoureusement à l'aide des dérivées.
Si la fonction qui nous intéresse est par contre plus exotique comme par exemple $\displaystyle f : x \mapsto \frac{x^4}{24} + \frac{p^2x^2}{4} - \frac{px^3}{6}$ (pour un paramètre $p$), il faudra tout de même calculer $\displaystyle f''(x) = \frac{x^2 + p^2}{2} - xp$ et montrer que $f''$ est positif pour démontrer que $f$ est convexe.
Il est cependant rare d'être dans un tel cas et une vérification graphique suffit généralement amplement. La connaissance des dérivées n'est donc pas du tout nécessaire pour continuer à explorer les inégalités !
Remarque : Les fonctions $f$ vérifiant $f''(x) = 0$ $\forall x \in I$ sont convexes et concaves. Il s'agit en fait des fonctions affines $f(x) = ax + b$ dont le graphe est une droite.
Exemples :
Définition
Une fonction $f:I\subseteq\mathbb{R}\to\mathbb{R}$ (où $I$ est un intervalle) est convexe sur $I$ si $\{(x,y) \in I \times \mathbb{R} \ | \ y \geq f(x)\}$ est convexe, c'est-à-dire si l'ensemble des points au dessus du graphe de $f$ forme un ensemble convexe.

Exemple de fonction convexe.
Une manière équivalente de définir la convexité est de dire qu'une fonction $f:I\subseteq\mathbb{R}\to\mathbb{R}$ est convexe sur $I$ si pour tous $a,b \in I$ et tout $\lambda \in [0,1]$, on a
$$f(\lambda a + (1-\lambda) b) \leq \lambda f(a) + (1-\lambda) f(b).$$ On remarque en effet que
$$(\lambda a + (1-\lambda) b, \lambda f(a) + (1-\lambda) f(b)) = \lambda (a, f(a)) + (1-\lambda) (b, f(b))$$ est le point du segment de droite reliant $(a,f(a))$ à $(b,f(b))$ d'abscisse $\lambda a + (1-\lambda) b$. Par ailleurs, $f(\lambda a + (1-\lambda) b)$ est la valeur de la fonction $f$ en ce même point. L'inégalité signifie donc que les segments de droite reliant deux points du graphe de $f$ ont tous leurs points au dessus du graphe.
Une fonction est par contre dite concave si l'ensemble des points en dessous du graphe de $f$ forme un ensemble convexe. Attention : cela ne revient pas à demander que l'ensemble des points au dessus du graphe est concave ! Contrairement aux ensembles qui sont soit convexes, soit concaves, il existe donc des fonctions qui ne sont ni convexes ni concaves.
Convexité et dérivée
Lorsqu'une fonction est (deux fois) dérivable, on peut facilement savoir si elle est convexe, concave, ou aucun des deux.Proposition
Soit $f: I \subseteq \mathbb{R} \to \mathbb{R}$ une fonction.
- Si $f$ est dérivable sur $I$, alors $f$ est convexe (respectivement concave) si et seulement si $f'$ est croissante (resp. décroissante) sur $I$.
- Si $f$ est deux fois dérivable, alors $f$ est convexe (respectivement concave) si et seulement si $f''(x) \geq 0$ (resp. $f''(x) \leq 0)$ $\forall x \in I$.
Lors d'une compétition, il n'est cependant pas réellement nécessaire de prouver qu'une fonction basique est concave ou convexe. En effet, on sait qu'il suffit de dériver deux fois la fonction pour démontrer qu'elle est convexe ou concave, ce qui se fait de manière automatique.
En pratique, on dessine le graphe de la fonction pour voir si elle est convexe ou concave en regardant l'ensemble délimité par le graphe. Il n'est donc pas important de connaître les dérivées : il faut juste retenir que la convexité ou concavité d'une fonction peut être vérifiée rigoureusement à l'aide des dérivées.
Si la fonction qui nous intéresse est par contre plus exotique comme par exemple $\displaystyle f : x \mapsto \frac{x^4}{24} + \frac{p^2x^2}{4} - \frac{px^3}{6}$ (pour un paramètre $p$), il faudra tout de même calculer $\displaystyle f''(x) = \frac{x^2 + p^2}{2} - xp$ et montrer que $f''$ est positif pour démontrer que $f$ est convexe.
Il est cependant rare d'être dans un tel cas et une vérification graphique suffit généralement amplement. La connaissance des dérivées n'est donc pas du tout nécessaire pour continuer à explorer les inégalités !
Remarque : Les fonctions $f$ vérifiant $f''(x) = 0$ $\forall x \in I$ sont convexes et concaves. Il s'agit en fait des fonctions affines $f(x) = ax + b$ dont le graphe est une droite.
Exemples :
- $f:\mathbb{R}\to\mathbb{R}:x\mapsto x^2$ est convexe car sa dérivée $f''(x) = 2$ est positive.
- $f:\mathbb{R}\to\mathbb{R}:x\mapsto e^x$ est convexe car sa dérivée $f''(x) = e^x$ est positive.
- $f:\mathbb{R}_0^+\to\mathbb{R}:x\mapsto \ln(x)$ est concave car sa dérivée $f''(x) = \frac{-1}{x^2}$ est négative.
3. Inégalité de Jensen
Lorsqu'on sait qu'une fonction est convexe ou concave (c'est-à-dire qu'on l'a vérifié graphiquement ou qu'on a calculé sa dérivée seconde), on peut utiliser l'inégalité de Jensen suivante, qui est en quelque sorte une généralisation de la définition de convexité (qui compare $f(\lambda x + (1-\lambda)y)$ avec $\lambda f(x) + (1-\lambda) f(y)$ où $\lambda \in [0, 1]$).
$$\sqrt[n]{a_1 a_2 \ldots a_n} \leq \frac{a_1 + a_2 + \ldots + a_n}{n} \quad \text{pour } \ a_1, \ldots, a_n \geq 0.$$ Si l'un des $a_i$ est nul, alors l'inégalité est évidente. Sinon, les deux membres sont strictement positifs. Dès lors, comme la fonction $\ln(x)$ est strictement croissante sur $\mathbb{R}_0^+$, c'est équivalent à
$$\ln(\sqrt[n]{a_1 a_2 \ldots a_n}) \leq \ln\left(\frac{a_1 + a_2 + \ldots + a_n}{n}\right)$$ ou encore
$$\frac{\ln(a_1) + \ln(a_2) + \ldots + \ln(a_n)}{n} \leq \ln\left(\frac{a_1 + a_2 + \ldots + a_n}{n}\right)$$ ce qui est vrai par l'inégalité de Jensen en prenant $f(x) = \ln(x)$ et $\lambda_i = \frac{1}{n}$ pour tout $i \in \{1, \ldots, n\}$ car $\ln(x)$ est concave et $\sum_{i=1}^n \frac{1}{n} = 1$.
Inégalité de Jensen
Soit $f:I\to\mathbb{R}$ une fonction.
Si $f$ est convexe sur $I$, alors pour tous $a_1, \ldots, a_n \in I$ et pour tous $\lambda_1, \lambda_2, \ldots, \lambda_n \in [0,1]$ tels que $\lambda_1 + \ldots + \lambda_n = 1$, on a
$$f\left(\lambda_1 a_1 + \ldots + \lambda_n a_n \right) \leq \lambda_1 f(a_1) + \ldots + \lambda_n f(a_n),$$ ce qui s'écrit, à l'aide des signes somme,
$$f\left(\sum_{i=1}^n \lambda_ia_i \right) \leq \sum_{i=1}^n \lambda_if(a_i).$$ Si $f$ est concave sur $I$, alors on a plutôt
$$f\left(\sum_{i=1}^n \lambda_ia_i\right) \geq \sum_{i=1}^n \lambda_if(a_i).$$
Si $f$ est convexe sur $I$, alors pour tous $a_1, \ldots, a_n \in I$ et pour tous $\lambda_1, \lambda_2, \ldots, \lambda_n \in [0,1]$ tels que $\lambda_1 + \ldots + \lambda_n = 1$, on a
$$f\left(\lambda_1 a_1 + \ldots + \lambda_n a_n \right) \leq \lambda_1 f(a_1) + \ldots + \lambda_n f(a_n),$$ ce qui s'écrit, à l'aide des signes somme,
$$f\left(\sum_{i=1}^n \lambda_ia_i \right) \leq \sum_{i=1}^n \lambda_if(a_i).$$ Si $f$ est concave sur $I$, alors on a plutôt
$$f\left(\sum_{i=1}^n \lambda_ia_i\right) \geq \sum_{i=1}^n \lambda_if(a_i).$$
Démonstration
On montre le cas où $f$ est convexe, l'autre cas étant similaire. On procède par récurrence.
- Pour $n = 2$, $\lambda_2 = 1 - \lambda_1$, et l'inégalité de Jensen devient alors
$$f(\lambda_1 a_1 + (1-\lambda_1) a_2) \leq \lambda_1 f(a_1) + (1-\lambda_1) f(a_2)$$ ce qui est exactement la définition de la convexité. - Supposons maintenant que l'inégalité de Jensen est vraie pour $n$ et montrons-la pour $n+1$. On doit donc prouver
$$f\left(\sum_{i=1}^n \lambda_ia_i + \lambda_{n+1}a_{n+1}\right) \leq \sum_{i=1}^n \lambda_if(a_i) + \lambda_{n+1}f(a_{n+1})$$ où $\displaystyle\sum_{i=1}^{n+1} \lambda_i = 1$. Si $\lambda_{n+1} = 0$, alors on a bien sûr déjà terminé. Par contre, on ne peut malheureusement pas appliquer l'hypothèse de récurrence sur les $(\lambda_1,\ldots,\lambda_n)$ dans le cas contraire car leur somme vaut $1-\lambda_{n+1}$ et non $1$. Une bonne idée est donc de poser $\displaystyle \lambda_i' = \frac{\lambda_i}{1-\lambda_{n+1}}$ pour $i \in \{1, \ldots, n\}$ de sorte que $\lambda'_1+\ldots+\lambda'_n=1$. L'inégalité à prouver devient alors
$$f\left((1-\lambda_{n+1})\sum_{i=1}^n \lambda_i'a_i + \lambda_{n+1}a_{n+1}\right) \leq (1-\lambda_{n+1})\sum_{i=1}^n \lambda_i'f(a_i) + \lambda_{n+1}f(a_{n+1}).$$ Par la définition de convexité, on a d'abord
$$f\left((1-\lambda_{n+1})\sum_{i=1}^n \lambda_i'a_i + \lambda_{n+1}a_{n+1}\right) \leq (1-\lambda_{n+1})f\left(\sum_{i=1}^n \lambda_i'a_i\right) + \lambda_{n+1}f(a_{n+1}),$$ et l'hypothèse de récurrence nous permet ensuite de conclure puisqu'elle nous donne
$$(1-\lambda_{n+1})f\left(\sum_{i=1}^n \lambda_i'a_i\right) + \lambda_{n+1}f(a_{n+1}) \leq (1-\lambda_{n+1})\sum_{i=1}^n \lambda_i'f(a_i) + \lambda_{n+1}f(a_{n+1}) = \sum_{i=1}^{n+1} \lambda_i f(a_i).$$
Exemple
On peut utiliser l'inégalité de Jensen pour montrer que la moyenne géométrique de plusieurs nombres est toujours inférieure ou égale à la moyenne arithmétique de ceux-ci :$$\sqrt[n]{a_1 a_2 \ldots a_n} \leq \frac{a_1 + a_2 + \ldots + a_n}{n} \quad \text{pour } \ a_1, \ldots, a_n \geq 0.$$ Si l'un des $a_i$ est nul, alors l'inégalité est évidente. Sinon, les deux membres sont strictement positifs. Dès lors, comme la fonction $\ln(x)$ est strictement croissante sur $\mathbb{R}_0^+$, c'est équivalent à
$$\ln(\sqrt[n]{a_1 a_2 \ldots a_n}) \leq \ln\left(\frac{a_1 + a_2 + \ldots + a_n}{n}\right)$$ ou encore
$$\frac{\ln(a_1) + \ln(a_2) + \ldots + \ln(a_n)}{n} \leq \ln\left(\frac{a_1 + a_2 + \ldots + a_n}{n}\right)$$ ce qui est vrai par l'inégalité de Jensen en prenant $f(x) = \ln(x)$ et $\lambda_i = \frac{1}{n}$ pour tout $i \in \{1, \ldots, n\}$ car $\ln(x)$ est concave et $\sum_{i=1}^n \frac{1}{n} = 1$.